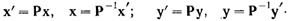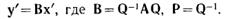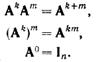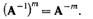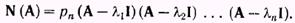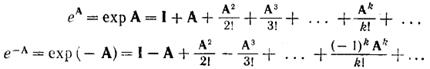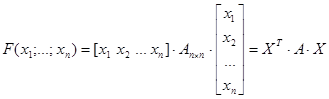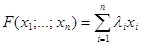По математическим основам теории систем

Реферат

По математическим основам теории систем

 

Выполнил:

Ивлев А.А.

Группа: ЗИЭФ-326

Проверил:

Разнополов О. А.

 

Челябинск

2014

Содержание:

 

Содержание

 

1. Матрицы и основные операции над ними                                                3

1.1. Понятие матрицы                                                                                   3

1.2. Виды матриц                                                                                           3

1.4. Действия над матрицами                                                                        3

1.5. Миноры и алгебраические дополнения                                                 4

1.6. Присоединенная и обратная матрицы                                                   4

1.7. Ранг матрицы и элементарные преобразования матрицы                   5

1.8. Вырожденность (дефект) матрицы                                                        5

2. Векторы и основные операции над ними                                                 5

2.1. Понятие вектора                                                                                     5

2.2. Основные операции над векторами                                                       5

3. Линейное векторное метрическое нормированное пространство           6

3.1. Понятия и определения                                                                          6

3.2. Линейное преобразование                                                                     7

3.3. Подпространство                                                                                    8

4. Матричные преобразования                                                                     8

4.1. Преобразование подобия                                                                       8

4.2. Ортогональное преобразование                                                            9

4.3. Конгруэнтное преобразование                                                              9

5. Собственные числа, собственные векторы и диагонализация матриц    9

5.1. Собственные числа и собственные векторы матрицы                          9

5.2. Диагонализация матриц                                                                         10

6. Функции от матриц                                                                                   11

6.1. Степени матриц                                                                                      11

6.2. Функции от матриц                                                                                12

6.3. Теоремы о функциях от матриц                                                            13

7. Квадратичная форма                                                                                 14

Список литературы                                                                                       16

Матрицы и основные операции над ними

Понятие матрицы

 

Матрицей А размером m´n или просто (m´n)-матрицей называют прямоугольную таблицу, содержащую m строк и n столбцов, элементами которой являются вещественные или комплексные числа.

2 матрицы одной и той же размерностью равны, если равны их соответствующие элементы.

 

Виды матриц

 

Матрицу называют столбцевой матрицей, если она состоит из одного столбца, то есть имеет размерность m´1.

Матрица называется строчной, если она имеет размерность 1´n.

Диагональная матрица – это такая квадратная матрица, все элементы которой, кроме расположенных на главной диагонали, равны нулю. Главная диагональ квадратной матрицы – это элементы aii, где i=1, 2,…, m.

Если все элементы матрицы равны нулю, то такая матрица называется нулевой. Если все элементы главной диагонали матрицы равны единице, то такая матрица называется единичной. Если все элементы главной диагонали матрицы равны одному и тому же числу, то такая матрица называется скалярной.

Квадратная матрица, все элементы ниже главной диагонали которой равны нулю, называется верхней треугольной матрицей. Квадратная матрица, все элементы выше главной диагонали которой равны нулю, называется нижней треугольной матрицей.

Квадратная матрица называется симметрической, если ее элементы удовлетворяют условию aij=aji.

 

Действия над матрицами

 

Суммой двух матриц A и B одной и той же размерности m´n называется матрица C размерности m´n, элементы которой находятся из условия cij=aij+bij.

Произведение матрицы A размерности m´n на число k – это такая матрица C размерности m´n, элементы которой находятся по формуле cij=k×aij.

Произведение согласованных матриц A размерностью m´n и B размерностью n´p называется матрица C размерностью m´p, элементы которой равны сумме произведений элементов i-ой строки матрицы A на элементы j-ой строки матрицы B:

Транспонированием матрицы A называется матрица, у которой строки и столбцы поменялись местами.

Пусть A(t) – матрица m´n, элементы которой aij(t) является дифференцируемыми функциями скалярной переменной t. Производная от A(t) по переменной t определяется как

Подобно произведению от матрицы интеграл от матрицы определяется как матрица, образованная из интегралов от элементов исходной матрицы:

Определитель квадратной матрицы A, записываемый как |A|, равен алгебраической сумме всех возможных произведений n элементов, содержащих лишь один элемент из каждой строки и столбца. При этом каждое из произведений положительно или отрицательно в соответствии со следующим правилом. Расположить все возможные произведения в порядке возрастания первых индексов, например, a13a22a31… Определить инверсию как расположение большего целого числа перед меньшим. Знак произведения является положительным, если число инверсий вторых индексов является четным; в противном случае он отрицательный. Например, последовательность 321 содержит три инверсии: 3 перед 2, 3 перед 1 и 2 перед 1.

 

Понятие вектора

 

Вектором или вектор-столбцом в n-мерном пространстве называется столбцевая матрица порядка n´1. Это не что иное, как распространение понятия векторов в двух- и трехмерных пространствах на n-мерное пространство. Если n больше трех, то геометрическое представление утрачивает свой смысл. Однако терминология, связанная с привычными координатными системами, тем не менее оказывается весьма полезной.

 

Подпространство

 

Рассмотрим произвольное конечное множество точек S={x1, …, xm} линейного пространства X. Множество

при всевозможных ai также представляет собой линейное пространство, являющееся подмножеством линейного пространства X и называемое линейным подпространством.

4. Матричные преобразования

 

Матрица B эквивалентна матрице А в том случае, если существуют такие две неособенные матрицы P и Q, что

B=PAQ.

 

4.1. Преобразовани е подобия

 

Рассмотрим линейное преобразование

y=Ax,

где x и y определяются в n-мерном пространстве с базисом zi. Предположим теперь, что требуется перейти от данного базиса к системе векторов wi. В этом состоит общая проблема преобразования координат. Пусть x и y соответственно переходят в новом базисе в координаты x’ и y’. Так как для zi и wi составляют два базисы в n-мерном пространстве, то должна существовать такая неособенная матрица P, что

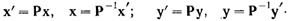
Найдем связь между y’ и x’ в новой системе координат. Для этого умножим слева обе части этого уравнения на P и получим Py=Pax. Из уравнения выше следует, что

или

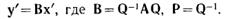
Матрица B, связывающая в новой системе координат x’ и y’, получается из A на основе преобразования подобия.

Преобразования подобия обладают важными свойствами:

1. Если матрица в одном базисе невырождена, то и в другом базисе она будет невырождена.

2. Определители, равно как и следы подобных матриц равны.

4.2. Ортогональное преобразование

Рассмотрим линейное преобразование

x=Qx’, P-1=Q,

где вектор x определяется в ортогональной системе координат. Если новая система координат также ортогональна, то длина вектора x’ в новой системе координат должна совпадать с длиной вектора x в первоначальной системе координат. Следовательно

<x, x>=<x’, x’>.

Выражая это соотношение посредством матрицы Q, имеем

Для этого необходимо, чтобы QT=Q-1.

Следовательно, при переходе от одного ортогонального базиса к другому матрица преобразования Q, ставящая в соответствие вектору в первоначальной системе координат вектор в новой системе координат, должна удовлетворят условию QT=Q-1. Данное преобразование называют ортогональным преобразованием. Матрица Q называется ортогональной матрицей. Ортогональное преобразование является частным случаем преобразования подобия. Оно оставляет неизменными длины и углы.

Из условия QT=Q-1 как следствие вытекает

|QT| |Q| = 1 или |Q| = ±1.

Знак минус в определителе означает, что ортогональное преобразование можно получить путем вращения или отражения. Косинусы углов между осью i' и осями 1, 2, …, n обозначаются соответственно элементами матрицы Q. Эти величины называются направляющими косинусами или направлениями новых осей по отношению к старым.

 

4.3. Конгруэнтное преобразование

 

Две матрицы называются конгруэнтными, если существует неособенная матрица Q, удовлетворяющая равенству

B=QTAQ.

Диагонализация матриц.

 

Для матрицы A, имеющей n различных характеристических чисел, преобразование вида M-1AM приводит к диагональной матрице D, где M называется модальной матрицей. Матрица M составлена из характеристических векторов матрицы A.

Однако матрица общего вида размерности (n´n) с кратными характеристическими числами может содержать меньше, чем n линейно независимых характеристических векторов; поэтому приведение к диагональной форме посредством преобразования может оказаться невозможным. Однако можно показать, что произвольная квадратная матрица путем преобразования подобия приводится к канонической матрице Жордана, обладающей следующими свойствами:

1. Диагональные элементы этой матрицы являются характеристическими числами A.

2. Все элементы, лежащие ниже главной диагонали, равны нулю.

3. Если соседние элементы на главной диагонали одинаковы, то элементы, непосредственно находящиеся справа от главной диагонали, равны единицы. Типичная жорданова форма имеет вид:

 

Заметим, что единицы встречаются в блоках вида

 

 

Они называются клетками Жордана.

Количество клеток Жордана, связанных с данным характеристическим числом li, в соответствии с преобразованием подобия, приводящим к жардановой форме, равное количеству собственных векторов, связанных с характеристическим числом, то есть q-дефекту [liI–A]. Однако, определить порядки клеток Жордана нелегко. Поэтому неясно, получается ли в результате преобразования J=M-1AM приведенная выше жорданова форма или форма

 

 

Полезно знать, что в случае полной вырожденности не будет присутствовать ни одной единицы. В случае простой вырожденности (q=1) все элементы, непосредственно лежащие справа от главной диагонали, равны единице. Для случаев, не укладывающихся в упомянутые, необходимо использовать для определения J и M метод проб и ошибок, основанный на равенстве

AM=MJ.

Пусть столбцы M обозначаются x1, x2, …, xn. Тогда существует клетка Жордана порядка m, связанная с lI лишь в том случае, если m линейно-независимых векторов x1, x2, …, xm удовлетворяют уравнениям:

Эти выражения применимы для каждой клетки Жордана.

Функции от матриц

Степени матриц

 

Произведение матриц AAA…A, где A – квадратная матрица порядка n, можно записать в виде Ak, где k означает число сомножителей, входящих в произведение. Это произведение называется k-й степенью матрицы A. Оно обладает свойствами

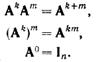
Те же правила справедливы при возведении матрицы в отрицательную степень при условии, что матрица неособенная, то есть существует обратная матрица. Имеем

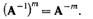
Подобные правила применяются и в случае вычисления дробной степени матрицы. Так, если Am=B, то A является корнем m-й степени B. Не существует общего правила определения, каким количеством корней степени m обладает матрица B, – число корней зависит от вида матрицы.

 

Функции от матриц

 

Матричный многочлен – это выражение вида

Разложение на множители этого многочлена, или факторизация матричного многчлена, имеет вид

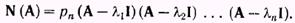
Бесконечный ряд матриц:

Геометрический ряд:

Экспоненциальная функция

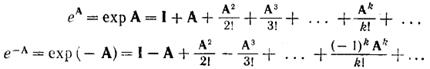
Можно показать, что этот ряд сходится равномерно и абсолютно. Произведение матричных экспонент:

eAeB=eA+B

Синусоидальная функция:

Косинусоидальная функция:

, где комплексная экспонента определяется как

Гиперболический синус

Гиперболический косинус

 

Квадратичная форма

 

Квадратичной формой называется выражение:

Этой квадратичной форме соответствует матрица

Сделаем следующее преобразование с каждым членом квадратичной формы:

a12x1x2+a21x2x1=x1x2(a12+a21)=0.5(a12+a11)x1x2+0.5(a12+a11)x1x2

Как видно, матрица, соответствующая этой квадратичной форме, является симметрической. Квадратичную форму можно представить в матричном виде:

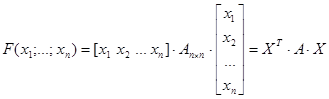
Квадратичная форма имеет канонический вид, если она содержит только квадраты переменных, то есть

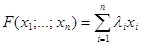
Ей соответствует диагональная матрица A=diag(lI). Следовательно, чтобы привести квадратичную форму к каноническому виду, нужно выполнить над ней такое преобразование, которое приведет матрицу, соответствующую ей, к каноническому виду, например, диагонализацию матрицы.

Если над квадратичной формой сделано некоторое линейное преобразование, то первоначальная и полученная квадратичные формы называются конгруэнтными.

Пусть над квадратичной формой сделано преобразование вида:

или короче Y=BX, где B=[bij]. Тогда квадратичная форма после преобразования принимает вид

F(Y)=YTAY

F(X)=(BX)TABX=XTBTABX=XTCX, где C=BTAB.

Квадратичная форма в независимости от выбора базиса в каноническом виде имеет одинаковое количество положительных и отрицательных коэффициентов.

Квадратичная форма называется положительно определенной, если для любого xÎR

F(X, X)>0

и отрицательно определенной, если для любого xÎR

F(X, X)<0.

В случае нестрогого неравенства квадратичная форма называется положительно полуопределенной и отрицательно полуопределенной соответственно.

Чтобы определить положительность квадратичной формы, служит критерий Сильвестра: квадратичная форма является положительно определенной тогда и только тогда, когда все угловые миноры матрицы, соответствующей этой квадратичной форме, положительны. Квадратичная форма является отрицательно определенной тогда и только тогда, когда угловые миноры матрицы, соответствующей этой квадратичной форме, будут чередоваться по знакам, начиная с отрицательного.

Список литературы

 

1. Коршунов Ю. М. Математические основы кибернетики. – М.: Энергоатомиздат, 1987.

2. Деруссо, Рой, Клоуз. Пространство состояний в теории систем.

 

Реферат

по математическим основам теории систем

 

Выполнил:

Ивлев А.А.

Группа: ЗИЭФ-326

Проверил:

Разнополов О. А.

 

Челябинск

2014

Содержание:

 

Содержание

 

1. Матрицы и основные операции над ними                                                3

1.1. Понятие матрицы                                                                                   3

1.2. Виды матриц                                                                                           3

1.4. Действия над матрицами                                                                        3

1.5. Миноры и алгебраические дополнения                                                 4

1.6. Присоединенная и обратная матрицы                                                   4

1.7. Ранг матрицы и элементарные преобразования матрицы                   5

1.8. Вырожденность (дефект) матрицы                                                        5

2. Векторы и основные операции над ними                                                 5

2.1. Понятие вектора                                                                                     5

2.2. Основные операции над векторами                                                       5

3. Линейное векторное метрическое нормированное пространство           6

3.1. Понятия и определения                                                                          6

3.2. Линейное преобразование                                                                     7

3.3. Подпространство                                                                                    8

4. Матричные преобразования                                                                     8

4.1. Преобразование подобия                                                                       8

4.2. Ортогональное преобразование                                                            9

4.3. Конгруэнтное преобразование                                                              9

5. Собственные числа, собственные векторы и диагонализация матриц    9

5.1. Собственные числа и собственные векторы матрицы                          9

5.2. Диагонализация матриц                                                                         10

6. Функции от матриц                                                                                   11

6.1. Степени матриц                                                                                      11

6.2. Функции от матриц                                                                                12

6.3. Теоремы о функциях от матриц                                                            13

7. Квадратичная форма                                                                                 14

Список литературы                                                                                       16