Определение. Число b называется пределом функции f (x) на бесконечности, если для любого числа 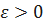 существует такое число N (
существует такое число N (  )>0, что
)>0, что 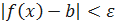 , как только
, как только  . В этом случае пишут
. В этом случае пишут  .
.
Если в данном определении условие  заменить на
заменить на 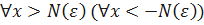 , то говорят, что b есть предел функции f (x) на плюс бесконечности (на минус бесконечности) и пишут:
, то говорят, что b есть предел функции f (x) на плюс бесконечности (на минус бесконечности) и пишут:  .
.
Следует отметить, что понятия БМФ и ББФ сохраняются и в этих случаях с поправкой на то, что аргумент функции становится бесконечно большим по абсолютной величине.
Примеры:
7.1.  Не существует.
Не существует.
7.2.  .
.
7.3. 
В примере 7.3 при вычислении предела возникает ситуация вида  , которая называется неопределенностью. Для устранения подобной ситуации следует числитель и знаменатель умножить на множитель, позволяющий свернуть числитель в разность определенных выражений.
, которая называется неопределенностью. Для устранения подобной ситуации следует числитель и знаменатель умножить на множитель, позволяющий свернуть числитель в разность определенных выражений.
7.4. Доказать, используя определение предела, что  .
.
Доказательство. Возьмем произвольно число 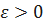 и рассмотрим абсолютную величину выражения
и рассмотрим абсолютную величину выражения  . Из последнего неравенства находим:
. Из последнего неравенства находим: 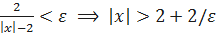 . Итак, если обозначить
. Итак, если обозначить  , то при
, то при  будет выполняться неравенство
будет выполняться неравенство 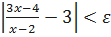 , а это значит, согласно определению предела, число 3 является пределом заданной функции.
, а это значит, согласно определению предела, число 3 является пределом заданной функции.
Асимптоты. Определение. Прямая y = kx + b называется асимптотой графика функции y= f (x) при  , если
, если  ; иными словами, если отклонение графика функции y= f (x) от прямой y = kx + b неограниченно уменьшается при
; иными словами, если отклонение графика функции y= f (x) от прямой y = kx + b неограниченно уменьшается при  . Аналогично можно определить асимптоту при
. Аналогично можно определить асимптоту при  .
.
Из данного определения вытекает, что если  , то y = b является горизонтальной асимптотой графика функции y = f (x). В том случае, когда
, то y = b является горизонтальной асимптотой графика функции y = f (x). В том случае, когда  , график функции не имеет горизонтальной асимптоты, но может иметь наклонную асимптоту y = kx + b, где
, график функции не имеет горизонтальной асимптоты, но может иметь наклонную асимптоту y = kx + b, где  . Так как в этом случае
. Так как в этом случае 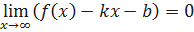 , то тем более
, то тем более  или
или  . Поэтому
. Поэтому  . Далее из равенства
. Далее из равенства 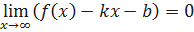 вытекает, что
вытекает, что  .
.
Таким образом, можно сформулировать следующий алгоритм поиска асимптот графика функции y = f (x):
1. Вычисляется  . Если этот предел существует и равен b, то y = b – горизонтальная асимптота; если
. Если этот предел существует и равен b, то y = b – горизонтальная асимптота; если  , то нужно перейти к следующему шагу.
, то нужно перейти к следующему шагу.
2. Вычисляется 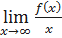 . Если этот предел не существует, то асимптоты нет, если предел существует и равен k, то следует перейти к следующему шагу.
. Если этот предел не существует, то асимптоты нет, если предел существует и равен k, то следует перейти к следующему шагу.
3. Вычисляется  . Если этот предел не существует, то асимптоты нет, если предел существует и равен b, то перейти к четвертому шагу.
. Если этот предел не существует, то асимптоты нет, если предел существует и равен b, то перейти к четвертому шагу.
4. Записать уравнение наклонной асимптоты y = kx + b.
Пример 7.5. Найти асимптоты графика функции 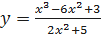 .
.
1.  ;
;
2. 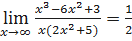 . Значит k =1/2;
. Значит k =1/2;
3.  , следовательно, b =-3;
, следовательно, b =-3;
4. y=0.5x-3.
Теорема 7.1. Для того чтобы число b было пределом функции f(x) при  необходимо и достаточно чтобы эта функция была представима в виде
необходимо и достаточно чтобы эта функция была представима в виде  , где
, где  -БМФ при
-БМФ при  .
.
Доказательство. Пусть b является пределом функции f (x) при  . Тогда для любого
. Тогда для любого  такое, что
такое, что  . Но
. Но  , поэтому
, поэтому  и следовательно
и следовательно  – БМФ при
– БМФ при 
Достаточность. Обратно, пусть теперь имеет место равенство  , где
, где  -БМФ при
-БМФ при  . Но тогда из определения БМФ следует, что b есть предел заданной функции при
. Но тогда из определения БМФ следует, что b есть предел заданной функции при  .
.
Теорема 7.2. Пусть функции f (x) и g (x) имеют в точке а пределы А и В соответственно. Тогда функции  имеют в точке a пределы равные
имеют в точке a пределы равные 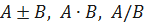 соответственно.
соответственно.
Доказательство. Пусть {xn} произвольная последовательность, сходящаяся к а. Тогда по определению предела функции по Гейне последовательности  сходятся к A и B соответственно. Используя соответствующие теоремы о сходимости последовательностей заключаем об истинности утверждения данной теоремы.
сходятся к A и B соответственно. Используя соответствующие теоремы о сходимости последовательностей заключаем об истинности утверждения данной теоремы.
Теорема 7.3. (Теорема о зажатой функции). Пусть функции  определены в некоторой окрестности точки а, за исключением, быть может, самой точки а, и функции
определены в некоторой окрестности точки а, за исключением, быть может, самой точки а, и функции  имеют, в точке а, предел равный A. Пусть, кроме того, выполняется неравенство
имеют, в точке а, предел равный A. Пусть, кроме того, выполняется неравенство 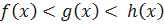 в некоторой окрестности точки а. Тогда
в некоторой окрестности точки а. Тогда  .
.
Доказательство. Доказательство основывается на определении предела по Гейне и на теореме о зажатой последовательности.
Замечание. Эти теоремы остаются верными и для случаев, когда 
Теорема 7.1 обычно используется при доказательстве существования предела если можно предсказать чему равен этот предел, а теорема 7.2 применяется когда необходимо вычислить предел сложных функций. Рассмотрим полезные примеры применения теоремы 7.3.
Пример 7.6. Первый замечательный предел  .
.
Докажем, что этот предел действительно равен 1. Рассмотрим числовую окружность единичного радиуса. В первой четверти выделим дугу AM, соответствующую центральному углу x (0< x < Pi /2). Из точки М опустим перпендикуляр на радиус ОА. Обозначим буквой К полученную точку на радиусе ОА. Из точки А проведем перпендикуляр к радиусу ОА до пересечения с прямой, полученной продолжением радиуса ОМ. Точку пересечения обозначим буквой N. Пусть  – площадь треугольника OAM,
– площадь треугольника OAM,  – площадь сектора OAM и
– площадь сектора OAM и  – площадь треугольника OAN. Очевидно неравенство
– площадь треугольника OAN. Очевидно неравенство 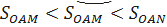 . Вычисляя указанные площади и подставляя полученные значения в неравенство, находим
. Вычисляя указанные площади и подставляя полученные значения в неравенство, находим
 .
.
Поделим это неравенство на 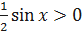 , так как
, так как 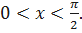 В результате получаем
В результате получаем  . Используя теорему 7.3, находим
. Используя теорему 7.3, находим  .
.
Из последнего соотношения и теоремы 7.2 получаем  . Найдем теперь левый предел, то есть
. Найдем теперь левый предел, то есть  (Так как функция
(Так как функция  четная). Так как предел справа и слева существуют и равны, то по теореме 6.2
четная). Так как предел справа и слева существуют и равны, то по теореме 6.2  ч.т.д.
ч.т.д.
Замечание. При доказательстве предполагалось, что 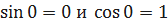 .
.
Пример 7.7. Второй замечательный предел 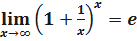 .
.
Доказательство. Пусть x >1. По принципу Архимеда существует такое натуральное n, что выполняется неравенство n < x < n +1. Поэтому можно записать 1+1/(n +1)<1+1/ x <1+1/ n. Учитывая это неравенство, нетрудно получить
 .
.
Очевидно, что  поэтому
поэтому  (Теорема 7.3).
(Теорема 7.3).
Рассмотрим теперь 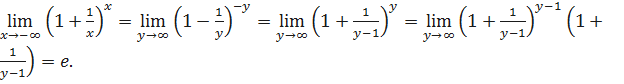 Объединяя оба случая, окончательно имеем
Объединяя оба случая, окончательно имеем  ч.т.д.
ч.т.д.
Лекция 8.



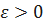 существует такое число N (
существует такое число N (  )>0, что
)>0, что 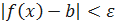 , как только
, как только  . В этом случае пишут
. В этом случае пишут  .
.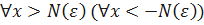 , то говорят, что b есть предел функции f (x) на плюс бесконечности (на минус бесконечности) и пишут:
, то говорят, что b есть предел функции f (x) на плюс бесконечности (на минус бесконечности) и пишут:  .
. Не существует.
Не существует. .
.
 , которая называется неопределенностью. Для устранения подобной ситуации следует числитель и знаменатель умножить на множитель, позволяющий свернуть числитель в разность определенных выражений.
, которая называется неопределенностью. Для устранения подобной ситуации следует числитель и знаменатель умножить на множитель, позволяющий свернуть числитель в разность определенных выражений. .
. . Из последнего неравенства находим:
. Из последнего неравенства находим: 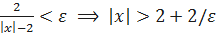 . Итак, если обозначить
. Итак, если обозначить  , то при
, то при  будет выполняться неравенство
будет выполняться неравенство 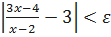 , а это значит, согласно определению предела, число 3 является пределом заданной функции.
, а это значит, согласно определению предела, число 3 является пределом заданной функции. , если
, если  ; иными словами, если отклонение графика функции y= f (x) от прямой y = kx + b неограниченно уменьшается при
; иными словами, если отклонение графика функции y= f (x) от прямой y = kx + b неограниченно уменьшается при  .
. , график функции не имеет горизонтальной асимптоты, но может иметь наклонную асимптоту y = kx + b, где
, график функции не имеет горизонтальной асимптоты, но может иметь наклонную асимптоту y = kx + b, где  . Так как в этом случае
. Так как в этом случае 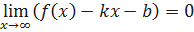 , то тем более
, то тем более  или
или  . Поэтому
. Поэтому  . Далее из равенства
. Далее из равенства  .
. . Если этот предел существует и равен b, то y = b – горизонтальная асимптота; если
. Если этот предел существует и равен b, то y = b – горизонтальная асимптота; если 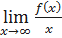 . Если этот предел не существует, то асимптоты нет, если предел существует и равен k, то следует перейти к следующему шагу.
. Если этот предел не существует, то асимптоты нет, если предел существует и равен k, то следует перейти к следующему шагу. . Если этот предел не существует, то асимптоты нет, если предел существует и равен b, то перейти к четвертому шагу.
. Если этот предел не существует, то асимптоты нет, если предел существует и равен b, то перейти к четвертому шагу.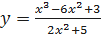 .
. ;
;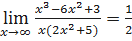 . Значит k =1/2;
. Значит k =1/2; , следовательно, b =-3;
, следовательно, b =-3; необходимо и достаточно чтобы эта функция была представима в виде
необходимо и достаточно чтобы эта функция была представима в виде  , где
, где  -БМФ при
-БМФ при  такое, что
такое, что  . Но
. Но  , поэтому
, поэтому  и следовательно
и следовательно 
 имеют в точке a пределы равные
имеют в точке a пределы равные 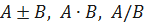 соответственно.
соответственно. сходятся к A и B соответственно. Используя соответствующие теоремы о сходимости последовательностей заключаем об истинности утверждения данной теоремы.
сходятся к A и B соответственно. Используя соответствующие теоремы о сходимости последовательностей заключаем об истинности утверждения данной теоремы. определены в некоторой окрестности точки а, за исключением, быть может, самой точки а, и функции
определены в некоторой окрестности точки а, за исключением, быть может, самой точки а, и функции  имеют, в точке а, предел равный A. Пусть, кроме того, выполняется неравенство
имеют, в точке а, предел равный A. Пусть, кроме того, выполняется неравенство 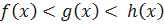 в некоторой окрестности точки а. Тогда
в некоторой окрестности точки а. Тогда  .
.
 .
. – площадь треугольника OAM,
– площадь треугольника OAM,  – площадь сектора OAM и
– площадь сектора OAM и  – площадь треугольника OAN. Очевидно неравенство
– площадь треугольника OAN. Очевидно неравенство 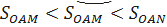 . Вычисляя указанные площади и подставляя полученные значения в неравенство, находим
. Вычисляя указанные площади и подставляя полученные значения в неравенство, находим .
.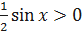 , так как
, так как 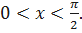 В результате получаем
В результате получаем  . Используя теорему 7.3, находим
. Используя теорему 7.3, находим  .
. . Найдем теперь левый предел, то есть
. Найдем теперь левый предел, то есть  (Так как функция
(Так как функция  четная). Так как предел справа и слева существуют и равны, то по теореме 6.2
четная). Так как предел справа и слева существуют и равны, то по теореме 6.2  ч.т.д.
ч.т.д.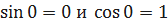 .
.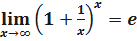 .
. .
. поэтому
поэтому  (Теорема 7.3).
(Теорема 7.3).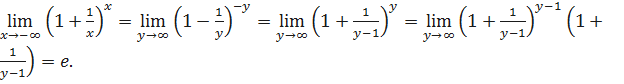 Объединяя оба случая, окончательно имеем
Объединяя оба случая, окончательно имеем  ч.т.д.
ч.т.д.

