Определение. Пусть дана функция 𝑓: 𝑋→𝑌. Если каждому 𝑦 ∈ 𝑌 соответствует единственное значение 𝑥 ∈ 𝑋, для которого 𝑦 = 𝑓(𝑥), то задана функция 𝜙: 𝑌→𝑋 такая, что 𝑥 = 𝜙(𝑦). Эта функция называется обратной к функции 𝑓(𝑥) и записывается в виде 𝑥 = 𝜙(𝑦) = 𝑓−1(𝑦).
Поскольку функция 𝑓(𝑥) является обратной к 𝑓−1(𝑥), то функции 𝑓(𝑥) и 𝑓−1(𝑥) еще называют взаимно обратными.
Для нахождения обратной функции 𝑦 = 𝑓−1(𝑥) следует решить уравнение 𝑦 = 𝑓(𝑥) относительно переменной 𝑥. Так, для функции 𝑦 = 2𝑥 существует обратная функция 𝑥 = 𝑦/2. Для функции 𝑦 = 𝑥2, заданной на отрезке [0, 1], существует обратная функция 𝑥 = √𝑦. Однако в случае, когда функция 𝑦 = 𝑥2 задана на отрезке [−1, 1], обратной функции не существует, поскольку одному значению 𝑦 может соответствовать несколько значений 𝑥. Например, значению 𝑦 = 1 соответствуют 𝑥1 = −1 и 𝑥2 = 1.
Предположим, что для функции 𝑦 = 𝑓(𝑥), заданной на отрезке [𝑎; 𝑏], существует обратная функция 𝑥 = 𝑓−1(𝑦). Пусть множеством значений функции 𝑓 является отрезок [𝑐; 𝑑]. Тогда, этот отрезок является областью определения обратной функции 𝑓−1, а отрезок [𝑎; 𝑏]—множеством ее значений. Графики функции 𝑦 = 𝑓(𝑥) и ее обратной 𝑥 = 𝑓−1(𝑦) будут совпадать, если в первом случае аргумент откладывать вдоль оси 𝑂𝑥, а во втором—вдоль оси 𝑂𝑦.
Если же условиться и в случае функции 𝑓, и в случае обратной функции 𝑓−1 независимую переменную обозначать через 𝑥, а зависимую—через 𝑦, то для того, чтобы получить график функции 𝑦 = 𝑓−1(𝑥) из графика 𝑦 = 𝑓(𝑥), нужно первый график зеркально отобразить относительно биссектрисы I и III четвертей координатной плоскости.
Теорема 5.1. Если функция f (x) строго монотонна на Х, то она обратима.
Доказательство. Пусть для определенности функция строго возрастает. Тогда для любых  таких, что
таких, что 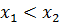 следует
следует  , а это значит каждому
, а это значит каждому 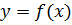 соответствует единственное
соответствует единственное  . Следовательно, задана обратная функция f -1 (y).
. Следовательно, задана обратная функция f -1 (y).
Определение. Пусть заданы функции 𝑓: 𝑋→𝑌 и 𝑔: 𝑌→𝑍. Функция 𝜙: 𝑋→𝑍, определяемая по формуле 𝜙(𝑥) = 𝑔(𝑓(𝑥)), называется сложной функцией, или суперпозицией функций 𝑦 = 𝑓(𝑥) и 𝑧 = 𝑔(𝑦).
Например, функция 𝑧=√cos(𝑥) является сложной функцией: суперпозицией тригонометрической функции 𝑦 = cos(𝑥) и степенной 𝑧 = 𝑦1/2. Функция 𝑦 = 𝑒2𝑥+1 также является сложной функцией: суперпозицией линейной функции 𝑡 = 2𝑥 + 1 и показательной 𝑦 = 𝑒𝑡.
Определение. Функция, заданная уравнением, не разрешенным относительно зависимой переменной, называется неявной.
Например, уравнение 𝑦3 + 𝑥2𝑦 − 2𝑥2 = 0 определяет 𝑦 как неявную функцию от 𝑥.
Пример. Для функции 𝑦 = ln(𝑥/2) найти обратную.
Решение. Очевидно, данная функция определена на промежутке (0;∞). Множеством ее значений является R. С помощью потенцирования находим 𝑒𝑦 = 𝑥/2. Значит, 𝑥 = 2𝑒𝑦 является обратной функцией к функции 𝑦 = ln(𝑥/2). Функция 𝑥 = 2𝑒𝑦 определена на R, а множеством ее значений является промежуток (0;+∞).
Пример на сложную функцию. Представить сложную функцию 𝑦 = arcsin(3𝑥) в виде суперпозиции соответствующих функций.
Решение. Данная сложная функция является суперпозицией степенной функции 𝑢 = 3𝑥 и обратной тригонометрической функции 𝑦 = arcsin(𝑢).
Элементарные функции
Значительную роль в математике и ее приложениях играет небольшой набор функций, которые принято называть основными элементарными функциями. Перечислим их.
1. Простейшей является постоянная функция 𝑦 = 𝐶.
2. Степенная функция имеет вид 𝑦 = 𝑥𝛼, где 𝛼 ∈ R. Примеры степенных функций с различными показателями: 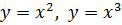 .
.
Первая функция означает, что для того чтобы получить y нужно x умножить на x. Область определения у этой функции - 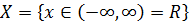 , а область значений -
, а область значений - 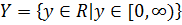 . Функция четная и, следовательно, ее график симметричен относительно оси OY. В области [0;
. Функция четная и, следовательно, ее график симметричен относительно оси OY. В области [0; 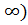 заданная функция строго монотонна (строго монотонно возрастает), то есть
заданная функция строго монотонна (строго монотонно возрастает), то есть 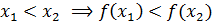 , так как
, так как 
 . Это значит, рассматриваемая функция имеет обратную
. Это значит, рассматриваемая функция имеет обратную 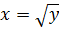 . Таким образом, определена операция возведение в степень ½ или взятие квадратного корня. Если рассмотреть функцию
. Таким образом, определена операция возведение в степень ½ или взятие квадратного корня. Если рассмотреть функцию 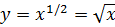 , то ее график будет зеркальным отражением функции
, то ее график будет зеркальным отражением функции  относительно биссектрисы угла первой четверти, при этом функция
относительно биссектрисы угла первой четверти, при этом функция 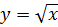 будет также строго монотонной.
будет также строго монотонной.
Аналогичные рассуждения можно провести и для функции 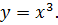 При этом устанавливается существование функции
При этом устанавливается существование функции 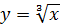 , которая является обратной к заданной.
, которая является обратной к заданной.
В общем случае можно говорить о степенной функции, у которой 𝛼=m/n – рациональное число. Если 𝛼 – иррациональное число, то его можно представить, как предел последовательности рациональных чисел и определить 𝑥𝛼 = 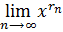 , где
, где 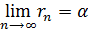 .
.
2. Показательная функция 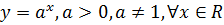 .
.
3. Обратная к показательной – логарифмическая функция, которая записывается так 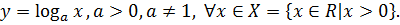
4. Тригонометрические функции 𝑦 = sin 𝑥 (синус), 𝑦 = cos 𝑥 (косинус), 𝑦 = tg𝑥 (тангенс) и 𝑦 = ctg𝑥 (котангенс) являются периодическими.
5. Обратные тригонометрические функции 𝑦 = arcsin𝑥 (арксинус), 𝑦 = arccos𝑥 (арккосинус), 𝑦 = arctg𝑥 (арктангенс) и 𝑦 = arcctg𝑥 (арккотангенс).
Определение. Функция, составленная из основных элементарных функций с помощью операций сложения, вычитания, умножения, деления и суперпозиции, называется элементарной функцией.
Определение. Простейшими элементарными функциями являются целая рациональная функция, или алгебраический многочлен
𝑃(𝑥) = 𝑎0𝑥𝑛 + 𝑎1𝑥𝑛−1 + 𝑎2𝑥𝑛−2 +... + 𝑎𝑛−2𝑥2 + 𝑎𝑛−1𝑥 + 𝑎𝑛, 𝑛 ∈ N,
а также дробная рациональная функция
𝑅(𝑥) = 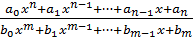 , 𝑛, m ∈ N
, 𝑛, m ∈ N
Множество целых и дробных рациональных функций образует класс рациональных функций.
Определение. Функции, не являющиеся элементарными, называются неэлементарными.
В качестве характерных примеров отметим неэлементарные функции 𝑦 = |𝑥| и 𝑦 = sign 𝑥.
В данном курсе мы сосредоточим внимание преимущественно на элементарных функциях.
Лекция 6.
Предел Функции.
6.1. Предел функции по Гейне.
Определение. Пусть функция f определена в некоторой окрестности точки x=a за исключением, быть может, самой точки a. Возьмем последовательность точек { xn } из этой окрестности, сходящуюся к точке a. Значения функции в точках последовательности, в свою очередь, образуют последовательность f(x1), f(x2),..., f(xn),.... Число b называется пределом функции f в точке x=a (или при x → a), если для любой последовательности { xn }, сходящейся к a и такой, что xn ̸=a для всех n ∈ N, соответствующая последовательность значений функции { f(xn) } сходится к b. Другими словами, число b называется пределом функции f в точке x=a, если ∀{ xn }, xn ̸=a (n ∈ N), 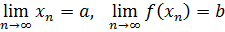 . Данное определение называется определением предела функции по Гейне, или на языке последовательностей. Предел функции f в точке x = a обозначается следующим образом:
. Данное определение называется определением предела функции по Гейне, или на языке последовательностей. Предел функции f в точке x = a обозначается следующим образом:
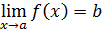
Определение. Число b называется пределом функции f при x →∞, или на бесконечности, если для любой ББП { xn } соответствующая последовательность значений функции { f(xn) } сходится к b. Для обозначения предела функции на бесконечности применяется запись:
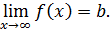
Пример 6.1. Постоянная функция f(x) = C в каждой точке имеет предел. Действительно, пусть a ∈ R и { xn }—произвольная последовательность, сходящаяся к a. Тогда ∀ n ∈ N f (xn) = C, и последовательность { f(xn) } будет иметь своим пределом число C.
Пример 6.2. Функция f(x) = sin(π/x) определена всюду на R, за исключением точки x = 0. Выясним, существует ли предел этой функции в точке x=0. С этой целью возьмем следующие две последовательности. Пусть первую последовательность составляют числа xn >0, где n = 0,1,2,..., такие, что sin(π/xn)=1, т.е. π/xn=(4n+1)π/2, xn=2/(4n+1). Очевидно, последовательность { xn } сходится к точке x = 0, а соответствующая последовательность значений функции будет состоять из единиц и иметь своим пределом число 1. Теперь возьмем другую последовательность значений аргумента { yn }, где yn > 0 и n ∈ N, такую, что sin(π/yn)=0, т.е. π/yn=nπ, yn=1/n, n ∈ N. Очевидно, в этом случае последовательность значений аргумента { yn } сходится к нулю, и соответствующая последовательность значения функции { sin(π/yn)} также сходится к нулю. Таким образом, в первом случае последовательность значений функции сходится к 1, а во втором к 0. Это означает, что у функции f(x)=sin(π/x) в точке x=0 предел не существует.
6.2. Предел функции по Коши.
Имеет место и другое определение предела функции в точке.
Определение. Число b называется пределом функции f в точке x=a, если для любого числа ε>0, сколь малым оно бы ни было, существует положительное число δ такое, что для всякого x, удовлетворяющего условию 0<|x−a|<δ, выполняется неравенство |f(x)−b|<ε. Другими словами, число b называется пределом функции f в точке x = a, если ∀ ε>0 ∃ δ>0: ∀ x, 0<|x−a|<δ, |f(x)−b|<ε. Это определение называется определением предела функции по Коши, или на языке ε-δ.
Можно доказать, что определения предела функции по Гейне и по Коши равносильны. Определение предела функции по Коши можно переформулировать следующим способом.
Определение. Число b называется пределом функции f в точке x = a, если для любой ε-окрестности точки b найдется такая δ-окрестность точки a, что для всех x ̸= a из этой δ-окрестности соответствующие значения функции f(x) лежат в ε-окрестности точки b. Это определение называется определением предела функции на языке окрестностей и выражает геометрический смысл предела функции.
Теорема 6.1. Определение предела по Гейне эквивалентно определению предела по Коши.
Доказательство. Пусть число b является пределом функции 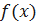 в точке a по Коши. Выберем произвольную подходящую последовательность
в точке a по Коши. Выберем произвольную подходящую последовательность 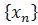 ,
, 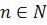 , то есть такую, для которой
, то есть такую, для которой 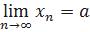 . Покажем, что b является пределом по Гейне. Зададим произвольное
. Покажем, что b является пределом по Гейне. Зададим произвольное 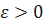 и укажем для него такое
и укажем для него такое 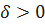 , что для всех x из условия
, что для всех x из условия 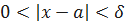 следует неравенство
следует неравенство 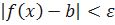 . В силу того, что
. В силу того, что 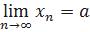 , для
, для 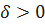 найдётся такой номер
найдётся такой номер 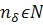 , что
, что 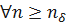 будет выполняться неравенство
будет выполняться неравенство 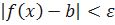 , то есть
, то есть 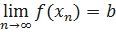 .
.
Докажем теперь обратное утверждение: предположим, что 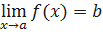 по Гейне, и покажем, что число b является пределом функции f (x) в точке a по Коши. Предположим, что это неверно, то есть:
по Гейне, и покажем, что число b является пределом функции f (x) в точке a по Коши. Предположим, что это неверно, то есть: 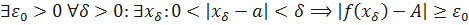 . В качестве
. В качестве 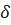 рассмотрим
рассмотрим 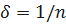 , а соответствующие значения
, а соответствующие значения 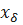 будем обозначать
будем обозначать 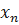 . Тогда при любом
. Тогда при любом 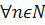 выполняются условия
выполняются условия 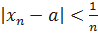 и
и 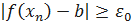 . Отсюда следует, что последовательность
. Отсюда следует, что последовательность 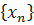 является подходящей, но число b не является пределом функции
является подходящей, но число b не является пределом функции 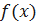 в точке a. Получили противоречие.
в точке a. Получили противоречие.
Односторонние пределы.
Определение. Число 𝑐 называется правым пределом функции 𝑓 в точке 𝑥=𝑎, если для любой сходящейся к 𝑎 последовательности {𝑦𝑛}, члены которой больше 𝑎, cсоответствующая последовательность {𝑓(𝑦𝑛)} сходится к 𝑐. Символически это записывается следующим образом: 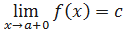 . Аналогичным образом определяется левый предел.
. Аналогичным образом определяется левый предел.
Определение. Число 𝑏 называется левым пределом функции 𝑓 в точке 𝑥=𝑎, если ∀{𝑥𝑛}, 𝑥𝑛<𝑎 (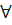 𝑛∈ N),
𝑛∈ N), 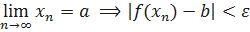 . В этом случае применяется обозначение:
. В этом случае применяется обозначение: 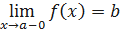 . В случае, когда 𝑎=0, используются обозначения:
. В случае, когда 𝑎=0, используются обозначения: 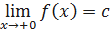 и
и 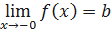 .
.
Определение. Правый и левый пределы функции в точке называются односторонними.
Определение. Число 𝑏 называется пределом функции 𝑓 при 𝑥→+∞, если для любой такой ББП {𝑥𝑛}, что 𝑥𝑛>0 для всех 𝑛∈ N, соответствующая последовательность {𝑓(𝑥𝑛)} сходится к 𝑏.
Аналогично определяется предел функции при 𝑥→−∞. Для записи таких пределов применяются обозначения:  ,
,  .
.
Сформулируем эти определения на языке 𝜀-𝛿. Число 𝑏 называется правым (левым) пределом функции 𝑓 в точке 𝑥=𝑎, если ∀𝜀>0 ∃𝛿>0: ∀𝑥, 𝑎<𝑥<𝑎+𝛿 (𝑎−𝛿<𝑥<𝑎), |𝑓(𝑥)−𝑏|<𝜀.
Пример 6.3. Функция 𝑦=sign(𝑥) имеет односторонние пределы в точке 𝑥=0. Очевидно,  и
и  .
.
Следующая теорема устанавливает связь между односторонними пределами и пределом функции.
Теорема 6.2. Для того чтобы функция 𝑓 имела предел в точке 𝑥=𝑎, необходимо и достаточно, чтобы существовали и были равны односторонние пределы в этой точке. В этом случае предел функции равен односторонним пределам: 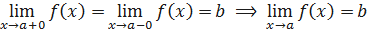 .
.
Доказательство. Необходимость. Пусть функция f (x) имеет предел равный b в точке x = a, то есть  . Так как x – любое то неравенство
. Так как x – любое то неравенство 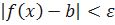 будет выполнено, если x взять слева от а:
будет выполнено, если x взять слева от а:  или справа от а:
или справа от а:  , а это означает существование односторонних пределов и их равенство b.
, а это означает существование односторонних пределов и их равенство b.
Достаточность. Пусть теперь существуют односторонние пределы функции f (x) и они равны b. Это значит, что для  и
и  . Таким образом, если положить
. Таким образом, если положить 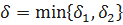 , то неравенство
, то неравенство 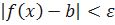 будет выполнено при любом x из интервала
будет выполнено при любом x из интервала 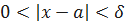 . Этот факт и доказывает существование предела функции f (x) равного b в точке x = a.
. Этот факт и доказывает существование предела функции f (x) равного b в точке x = a.
Бесконечно малые функции
Определение. Функция 𝛼(𝑥) называется бесконечно малой при 𝑥→𝑎 (БМФ), если ∀𝜀>0 ∃𝛿>0: ∀𝑥, 0<|𝑥−𝑎|<𝛿, |𝛼(𝑥)|<𝜀. 
Согласно определению предела функции по Коши функция 𝛼(𝑥) является бесконечно малой при 𝑥 → 𝑎 тогда и только тогда, когда. Обратим внимание на необходимость указания точки, в которой функция является бесконечно малой. Например, функция 𝑦=𝑥2 является бесконечно малой при 𝑥→0, но не является бесконечно малой при 𝑥→1. В самом деле,  , а
, а  .
.
Свойства БМФ
1. Сумма любого конечного числа БМФ есть БМФ.
Доказательство. Достаточно доказать это свойство для двух функций. Итак, пусть 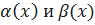 – БМФ при 𝑥→ a. Тогда для любого
– БМФ при 𝑥→ a. Тогда для любого  и
и  . Рассмотрим выражение
. Рассмотрим выражение  , где
, где  . А это означает, по Коши, что
. А это означает, по Коши, что  .
.
2. Бесконечно малая функция при 𝑥→𝑎 является ограниченной в некоторой окрестности точки 𝑎.
Доказательство. Непосредственно следует из определения при 
3. Произведение бесконечно малой функции при 𝑥→𝑎 и функции, ограниченной в некоторой окрестности точки 𝑎, есть бесконечно малая функция при 𝑥→𝑎.
Доказательство. Пусть-  – БМФ при 𝑥→ a и f (x) – ограниченная функция в некоторой окрестности точки а. Рассмотрим функцию вида
– БМФ при 𝑥→ a и f (x) – ограниченная функция в некоторой окрестности точки а. Рассмотрим функцию вида 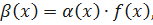 когда 𝑥→ a. Для любого
когда 𝑥→ a. Для любого  такое, что
такое, что  , как только х попадет в
, как только х попадет в 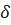 – окрестность точки а, то есть
– окрестность точки а, то есть 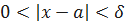 . Кроме того, так как
. Кроме того, так как  ограничена в некоторой окрестности точки а, то найдется такое М>0, что можно записать
ограничена в некоторой окрестности точки а, то найдется такое М>0, что можно записать  . Следовательно,
. Следовательно,  ч.т.д.
ч.т.д.
4. Произведение нескольких БМФ есть БМФ. Доказательство. Непосредственно следует из определения
5. Произведение БМФ на постоянную есть БМФ. Доказательство. На основе свойства 3.
Бесконечно большие функции.
Определение. Функция f(x) называется бесконечно большой при x→a (ББФ), если для любого числа A>0, сколь большим оно бы ни было, существует такое δ>0, что для всех x, удовлетворяющих условию 0<|x−a|<δ, выполнено неравенство |f(x)|>A, т.е. ∀ A>0 ∃ δ>0: ∀ x, 0<|x−a|<δ, |f(x)|>A. В этом случае применяется обозначение:  . Если известно, что при 0<|x−a|<δ функция f(x) принимает только положительные (отрицательные) значения, данное обозначение может быть дополнено путем указания знака бесконечности:
. Если известно, что при 0<|x−a|<δ функция f(x) принимает только положительные (отрицательные) значения, данное обозначение может быть дополнено путем указания знака бесконечности:  (
(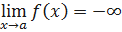 ).
).
Не следует забывать указывать точку, в которой функция является бесконечно большой. Например, функция y=1/(x−2) является бесконечно большой при x→2, но не является бесконечно большой при x→1.


 таких, что
таких, что 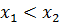 следует
следует  , а это значит каждому
, а это значит каждому 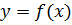 соответствует единственное
соответствует единственное  . Следовательно, задана обратная функция f -1 (y).
. Следовательно, задана обратная функция f -1 (y).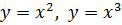 .
.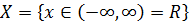 , а область значений -
, а область значений - 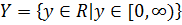 . Функция четная и, следовательно, ее график симметричен относительно оси OY. В области [0;
. Функция четная и, следовательно, ее график симметричен относительно оси OY. В области [0; 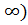 заданная функция строго монотонна (строго монотонно возрастает), то есть
заданная функция строго монотонна (строго монотонно возрастает), то есть 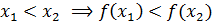 , так как
, так как 
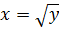 . Таким образом, определена операция возведение в степень ½ или взятие квадратного корня. Если рассмотреть функцию
. Таким образом, определена операция возведение в степень ½ или взятие квадратного корня. Если рассмотреть функцию 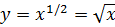 , то ее график будет зеркальным отражением функции
, то ее график будет зеркальным отражением функции  относительно биссектрисы угла первой четверти, при этом функция
относительно биссектрисы угла первой четверти, при этом функция 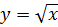 будет также строго монотонной.
будет также строго монотонной.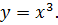 При этом устанавливается существование функции
При этом устанавливается существование функции 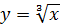 , которая является обратной к заданной.
, которая является обратной к заданной.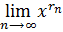 , где
, где 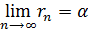 .
.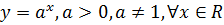 .
.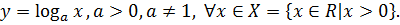
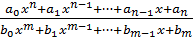 , 𝑛, m ∈ N
, 𝑛, m ∈ N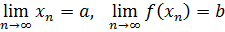 . Данное определение называется определением предела функции по Гейне, или на языке последовательностей. Предел функции f в точке x = a обозначается следующим образом:
. Данное определение называется определением предела функции по Гейне, или на языке последовательностей. Предел функции f в точке x = a обозначается следующим образом: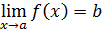
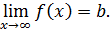
 в точке a по Коши. Выберем произвольную подходящую последовательность
в точке a по Коши. Выберем произвольную подходящую последовательность  ,
, 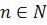 , то есть такую, для которой
, то есть такую, для которой 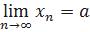 . Покажем, что b является пределом по Гейне. Зададим произвольное
. Покажем, что b является пределом по Гейне. Зададим произвольное 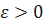 и укажем для него такое
и укажем для него такое 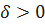 , что для всех x из условия
, что для всех x из условия 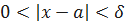 следует неравенство
следует неравенство 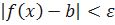 . В силу того, что
. В силу того, что 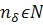 , что
, что 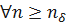 будет выполняться неравенство
будет выполняться неравенство 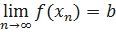 .
.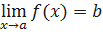 по Гейне, и покажем, что число b является пределом функции f (x) в точке a по Коши. Предположим, что это неверно, то есть:
по Гейне, и покажем, что число b является пределом функции f (x) в точке a по Коши. Предположим, что это неверно, то есть: 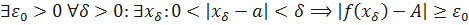 . В качестве
. В качестве 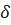 рассмотрим
рассмотрим 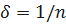 , а соответствующие значения
, а соответствующие значения 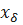 будем обозначать
будем обозначать 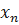 . Тогда при любом
. Тогда при любом 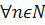 выполняются условия
выполняются условия 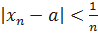 и
и 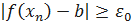 . Отсюда следует, что последовательность
. Отсюда следует, что последовательность 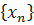 является подходящей, но число b не является пределом функции
является подходящей, но число b не является пределом функции 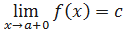 . Аналогичным образом определяется левый предел.
. Аналогичным образом определяется левый предел.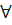 𝑛∈ N),
𝑛∈ N), 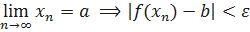 . В этом случае применяется обозначение:
. В этом случае применяется обозначение: 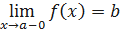 . В случае, когда 𝑎=0, используются обозначения:
. В случае, когда 𝑎=0, используются обозначения: 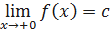 и
и 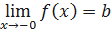 .
. ,
,  .
. и
и  .
.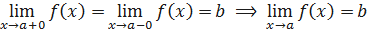 .
. . Так как x – любое то неравенство
. Так как x – любое то неравенство  или справа от а:
или справа от а:  , а это означает существование односторонних пределов и их равенство b.
, а это означает существование односторонних пределов и их равенство b. и
и  . Таким образом, если положить
. Таким образом, если положить 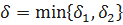 , то неравенство
, то неравенство 
 , а
, а  .
.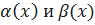 – БМФ при 𝑥→ a. Тогда для любого
– БМФ при 𝑥→ a. Тогда для любого  и
и  . Рассмотрим выражение
. Рассмотрим выражение  , где
, где  . А это означает, по Коши, что
. А это означает, по Коши, что  .
.
 – БМФ при 𝑥→ a и f (x) – ограниченная функция в некоторой окрестности точки а. Рассмотрим функцию вида
– БМФ при 𝑥→ a и f (x) – ограниченная функция в некоторой окрестности точки а. Рассмотрим функцию вида 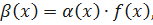 когда 𝑥→ a. Для любого
когда 𝑥→ a. Для любого  такое, что
такое, что  , как только х попадет в
, как только х попадет в  ограничена в некоторой окрестности точки а, то найдется такое М>0, что можно записать
ограничена в некоторой окрестности точки а, то найдется такое М>0, что можно записать  . Следовательно,
. Следовательно,  ч.т.д.
ч.т.д. . Если известно, что при 0<|x−a|<δ функция f(x) принимает только положительные (отрицательные) значения, данное обозначение может быть дополнено путем указания знака бесконечности:
. Если известно, что при 0<|x−a|<δ функция f(x) принимает только положительные (отрицательные) значения, данное обозначение может быть дополнено путем указания знака бесконечности:  (
(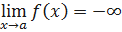 ).
).


