Числовая последовательность.
Определение. Пусть N —множество натуральных чисел. Если каждому натуральному числу  по определенному правилу поставлено в соответствие некоторое число
по определенному правилу поставлено в соответствие некоторое число  , то говорят, что определена числовая последовательность. Числа
, то говорят, что определена числовая последовательность. Числа  при 𝑛 ∈ N, называют элементами, или членами последовательности. Для числовой последовательности будем так же использовать следующие обозначения:
при 𝑛 ∈ N, называют элементами, или членами последовательности. Для числовой последовательности будем так же использовать следующие обозначения: 
 или {
или {  };
};  .
.
Пример. Последовательности уже встречались в программе по математики в средней школе, например, бесконечная геометрическая прогрессия вида:
 , является числовой последовательностью. Числовой последовательностью является и арифметическая прогрессия:
, является числовой последовательностью. Числовой последовательностью является и арифметическая прогрессия: 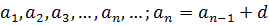 ,
,  ,
,  – заданные числа из R.
– заданные числа из R.
Определение. Последовательности 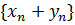 ,
,  ,
,  ,
,  называются соответственно суммой, разностью, произведением и частным двух последовательностей {
называются соответственно суммой, разностью, произведением и частным двух последовательностей {  } и {
} и { 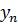 } (для частного
} (для частного  ,
,  ).
).
Определение. Последовательность {  } называется ограниченной, если существует такое число 𝑀>0, что для любого 𝑛 ∈ N выполняется неравенство
} называется ограниченной, если существует такое число 𝑀>0, что для любого 𝑛 ∈ N выполняется неравенство 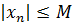 .
.
Определение. Окрестностью точки называется любой интервал, содержащий эту точку. -окрестностью точки 𝑥 = 𝑎 называется интервал (𝑎 − 𝜀; 𝑎 + 𝜀).
Геометрической смысл ограниченной последовательности состоит в том, что все члены последовательности находятся в некоторой окрестности (𝑀-окрестности) точки 𝑥 = 0 (рисунок 3.1).
__ - M _____  _______________
_______________  ___ 0 ______
___ 0 ______  __________
__________  _______ M _
_______ M _
Рис.3.1
Определение. Последовательность {  } называется неограниченной, если она не является ограниченной. Это значит что для любого 𝑀>0, каким бы большим оно ни было, найдется такое число 𝑛 ∈ N, для которого будет |
} называется неограниченной, если она не является ограниченной. Это значит что для любого 𝑀>0, каким бы большим оно ни было, найдется такое число 𝑛 ∈ N, для которого будет |  | > 𝑀. На языке кванторов это определение будет выглядеть следующим образом: ∀𝑀 > 0 ∃ 𝑛 ∈ N: |
| > 𝑀. На языке кванторов это определение будет выглядеть следующим образом: ∀𝑀 > 0 ∃ 𝑛 ∈ N: |  | > 𝑀.
| > 𝑀.
Например:
а) последовательность

ограничена, так как ∀ 𝑛 ∈ N верно, что |  | =1/ n и, следовательно,
| =1/ n и, следовательно, 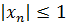 .
.
б) последовательность  . является неограниченной, так как, каково бы ни было число 𝑀 > 0, ∃
. является неограниченной, так как, каково бы ни было число 𝑀 > 0, ∃  =
=  такое, что
такое, что  >𝑀.
>𝑀.
Определение. Последовательность  называется постоянной, если ∃ 𝑎 ∈ R, что ∀ 𝑛 ∈ N
называется постоянной, если ∃ 𝑎 ∈ R, что ∀ 𝑛 ∈ N  = 𝑎, то есть все элементы последовательности равны некоторому числу 𝑎.
= 𝑎, то есть все элементы последовательности равны некоторому числу 𝑎.
Например, последовательность 1, 1,..., 1,... является постоянной. Здесь ∀ 𝑛 ∈ N имеет место равенство  = 1.
= 1.
Предел последовательности
Изучение предела последовательности — основного понятия этого параграфа, начнем с наводящего примера. Рассмотрим последовательность 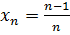 ; или
; или 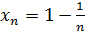 . Из последнего выражения видно, что с увеличением n числа
. Из последнего выражения видно, что с увеличением n числа  приближаются к значению a =1. Действительно, оценим степень близости элемента
приближаются к значению a =1. Действительно, оценим степень близости элемента  к 1:
к 1: 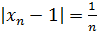 и с увеличением n расстояние между элементами последовательности и числом 1 неограниченно сокращается. В таком случае говорят, что число 1 является пределом последовательности {
и с увеличением n расстояние между элементами последовательности и числом 1 неограниченно сокращается. В таком случае говорят, что число 1 является пределом последовательности {  }.
}.
Получив, на конкретном примере, представление о сути предельного перехода, мы готовы перейти к математически строгому определению предела.
Определение. Число 𝑎 называется пределом последовательности {  }, если для всякого числа 𝜀 > 0, сколь малым оно бы ни было, существует номер
}, если для всякого числа 𝜀 > 0, сколь малым оно бы ни было, существует номер 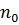 ∈ N такой, что для всех 𝑛 >
∈ N такой, что для всех 𝑛 > 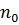 имеет место неравенство |
имеет место неравенство |  −𝑎|<𝜀. На языке кванторов это выглядит так: ∀ 𝜀 > 0 ∃
−𝑎|<𝜀. На языке кванторов это выглядит так: ∀ 𝜀 > 0 ∃ 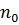 ∈ N: ∀ 𝑛 >
∈ N: ∀ 𝑛 > 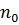 |
|  −𝑎|<𝜀.
−𝑎|<𝜀.
Для обозначения предела используется выражение 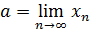 .
.
Пример. Пусть дана последовательность  . Доказать, что пределом последовательности является число a =1/2, используя определение предела.
. Доказать, что пределом последовательности является число a =1/2, используя определение предела.
Решение. Рассмотрим величину 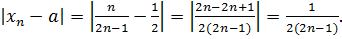 Возьмем произвольное 𝜀 > 0 и запишем неравенство
Возьмем произвольное 𝜀 > 0 и запишем неравенство 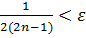 . Решая это неравенство, находим
. Решая это неравенство, находим 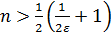 . Обозначим
. Обозначим 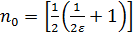 +1, тогда при
+1, тогда при 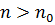 будет выполняться неравенство
будет выполняться неравенство 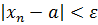 ч.т.д.
ч.т.д.
Если последовательность имеет конечный предел, то говорят, что она сходится. В противном случае – расходится.
Бесконечно малые последовательности.
Если последовательность сходится и ее предел равен 0, то она называется бесконечно малой. Пользуясь определением предела, можно дать определение бесконечно малой последовательности на языке 𝜀.
Определение. Последовательность 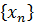 называется бесконечно малой если ∀ 𝜀 > 0 ∃
называется бесконечно малой если ∀ 𝜀 > 0 ∃ 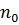 ∈ N: ∀ 𝑛 >
∈ N: ∀ 𝑛 > 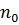 |
|  |<𝜀.
|<𝜀.
Свойства бесконечно малых последовательностей (БМП):
1. Сумма конечного числа бесконечно малых последовательностей есть БМП. [Доказательство]
2. Бесконечно малая последовательность является ограниченной. [Доказательство]
3. Произведение бесконечно малой последовательности и ограниченной последовательности есть БМП. [Доказательство]
4. Произведение нескольких БМП есть БМП. [Доказательство]
5. Если БМП {  } имеет постоянное значение 𝑎, т.е. ∀ 𝑛 ∈ N верно, что
} имеет постоянное значение 𝑎, т.е. ∀ 𝑛 ∈ N верно, что 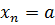 , то 𝑎 = 0. [Доказательство]
, то 𝑎 = 0. [Доказательство]
Бесконечно большие последовательности (ББП).
Определение. Последовательность 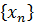 называется бесконечно большой, если для любого числа А>0, каким бы большим оно ни было, найдется такой номер
называется бесконечно большой, если для любого числа А>0, каким бы большим оно ни было, найдется такой номер 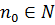 , что при
, что при 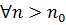 выполняется неравенство
выполняется неравенство 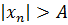 . При этом пишут
. При этом пишут 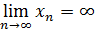 .
.
Если окажется, что при любом А>0 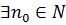 такой, что
такой, что 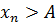
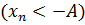 при
при 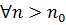 , то пишут
, то пишут 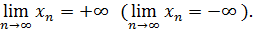
Свойства бесконечно больших последовательностей.
1. ББП—неограниченная последовательность.
2. Произведение двух ББП есть ББП.
3. Сумма ББП и ограниченной последовательности есть ББП.
4. ББП не может являться постоянной последовательностью.
Замечание. Сумма двух ББП не обязательно является ББП. Например, последовательности 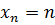 и
и 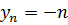 бесконечно большие. Однако, сумма
бесконечно большие. Однако, сумма  +
+ 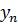 =0 бесконечно большой не является.
=0 бесконечно большой не является.
Последовательности БМП и ББП связаны между собой. На это указывает следующая теорема.
ТЕОРЕМА 3.1. Если {  } есть ББП и все ее члены отличны от нуля, то последовательность {1/
} есть ББП и все ее члены отличны от нуля, то последовательность {1/  } есть БМП; и обратно, если {
} есть БМП; и обратно, если {  }—БМП, все члены которой отличны от нуля, то {1/
}—БМП, все члены которой отличны от нуля, то {1/  }—ББП.
}—ББП.
Доказательство. Пусть {  } есть ББП. Это значит, что для любого A >0 в том числе и для A =1/𝜀
} есть ББП. Это значит, что для любого A >0 в том числе и для A =1/𝜀 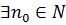 такой, что при
такой, что при 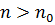 выполняется неравенство
выполняется неравенство 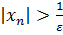 . Из этого неравенства сразу следует, что
. Из этого неравенства сразу следует, что 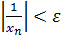 ч.т.д. Обратное утверждение доказывается аналогично.
ч.т.д. Обратное утверждение доказывается аналогично.



 по определенному правилу поставлено в соответствие некоторое число
по определенному правилу поставлено в соответствие некоторое число  , то говорят, что определена числовая последовательность. Числа
, то говорят, что определена числовая последовательность. Числа  при 𝑛 ∈ N, называют элементами, или членами последовательности. Для числовой последовательности будем так же использовать следующие обозначения:
при 𝑛 ∈ N, называют элементами, или членами последовательности. Для числовой последовательности будем так же использовать следующие обозначения: 
 или {
или {  };
};  , является числовой последовательностью. Числовой последовательностью является и арифметическая прогрессия:
, является числовой последовательностью. Числовой последовательностью является и арифметическая прогрессия: 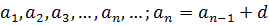 ,
,  ,
,  – заданные числа из R.
– заданные числа из R.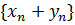 ,
,  ,
,  ,
,  называются соответственно суммой, разностью, произведением и частным двух последовательностей {
называются соответственно суммой, разностью, произведением и частным двух последовательностей { 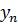 } (для частного
} (для частного  ,
, 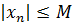 .
. _______________
_______________  ___ 0 ______
___ 0 ______  __________
__________  _______ M _
_______ M _
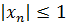 .
. . является неограниченной, так как, каково бы ни было число 𝑀 > 0, ∃
. является неограниченной, так как, каково бы ни было число 𝑀 > 0, ∃  такое, что
такое, что  называется постоянной, если ∃ 𝑎 ∈ R, что ∀ 𝑛 ∈ N
называется постоянной, если ∃ 𝑎 ∈ R, что ∀ 𝑛 ∈ N 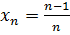 ; или
; или 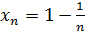 . Из последнего выражения видно, что с увеличением n числа
. Из последнего выражения видно, что с увеличением n числа 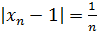 и с увеличением n расстояние между элементами последовательности и числом 1 неограниченно сокращается. В таком случае говорят, что число 1 является пределом последовательности {
и с увеличением n расстояние между элементами последовательности и числом 1 неограниченно сокращается. В таком случае говорят, что число 1 является пределом последовательности { 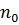 ∈ N такой, что для всех 𝑛 >
∈ N такой, что для всех 𝑛 > 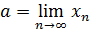 .
. . Доказать, что пределом последовательности является число a =1/2, используя определение предела.
. Доказать, что пределом последовательности является число a =1/2, используя определение предела.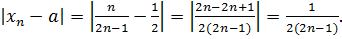 Возьмем произвольное 𝜀 > 0 и запишем неравенство
Возьмем произвольное 𝜀 > 0 и запишем неравенство 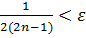 . Решая это неравенство, находим
. Решая это неравенство, находим 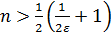 . Обозначим
. Обозначим 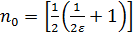 +1, тогда при
+1, тогда при 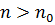 будет выполняться неравенство
будет выполняться неравенство 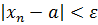 ч.т.д.
ч.т.д.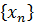 называется бесконечно малой если ∀ 𝜀 > 0 ∃
называется бесконечно малой если ∀ 𝜀 > 0 ∃ 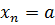 , то 𝑎 = 0. [Доказательство]
, то 𝑎 = 0. [Доказательство]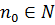 , что при
, что при 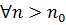 выполняется неравенство
выполняется неравенство 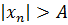 . При этом пишут
. При этом пишут 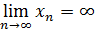 .
.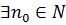 такой, что
такой, что 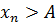
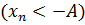 при
при 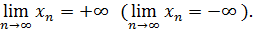
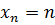 и
и 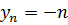 бесконечно большие. Однако, сумма
бесконечно большие. Однако, сумма 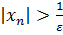 . Из этого неравенства сразу следует, что
. Из этого неравенства сразу следует, что 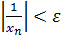 ч.т.д. Обратное утверждение доказывается аналогично.
ч.т.д. Обратное утверждение доказывается аналогично.

