Пусть 
 – дифференцируемые функции,
– дифференцируемые функции, 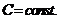
Производные высших порядков
Производная  функции
функции  тоже есть функция от x и называется производной 1-го порядка (1-й производной).
тоже есть функция от x и называется производной 1-го порядка (1-й производной).
Если функция  дифференцируемая, то ее производ-ная называется производной 2-го порядка (2-й производной) и обозначается
дифференцируемая, то ее производ-ная называется производной 2-го порядка (2-й производной) и обозначается  ,
,  или
или  .
.
Производная от производной 2-го порядка, если она существует, называется производной 3-го порядка и обоз-начается  ,
,  или
или  .
.
По индукции производной n-го порядка называется про-изводная от производной (n -1) порядка:  ,
,  .
.
Производные функции порядка выше первого называются производными высших порядков.
Например,для функции  имеем:
имеем:  ;
;  ;
; 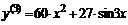 и т. д.
и т. д.
Пример 9.11. Найти производную 2-го порядка функции  .
.
Решение. Поскольку  , то
, то 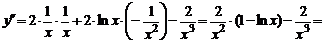
 .
.
Если функция задана параметрически:  ,
,  ,
,  , функции
, функции 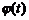 ,
,  дифференцируемые, по крайней мере, n -го порядка включительно,
дифференцируемые, по крайней мере, n -го порядка включительно,  , тогда производные
, тогда производные  ,
,  ,
,  , … вычисляются по формулам:
, … вычисляются по формулам:

 ,
,  и т. д.
и т. д.
Например, для функции  ,
,  имеем:
имеем:
 ;
;  .
.
Теоремы о дифференцируемости функции
Знание производной дифференцируемой функции в лю-бой точке интервала  часто позволяет делать выводы о по-ведении на нем самой функции. Обоснованию этого заявления и посвящена оставшаяся часть пособия.
часто позволяет делать выводы о по-ведении на нем самой функции. Обоснованию этого заявления и посвящена оставшаяся часть пособия.
Теорема 9.3 (Фермá). Если функция 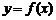 определена и непрерывна на отрезке
определена и непрерывна на отрезке  , достигает наибольшего (наи-меньшего) значения в точке
, достигает наибольшего (наи-меньшего) значения в точке  и имеет в ней конечную производную, то производная функции в этой точке равна нулю, то есть
и имеет в ней конечную производную, то производная функции в этой точке равна нулю, то есть  .
.
Теорема 9.4 (Рóлля). Если функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке  , дифференцируема на интервале
, дифференцируема на интервале  и на концах промежутка принимает равные значения
и на концах промежутка принимает равные значения  , то существует хотя бы одна точка
, то существует хотя бы одна точка  , производная функции в которой равна нулю, то есть
, производная функции в которой равна нулю, то есть  .
.
Теорема 9.5 (Лагранжа). Если функция  опреде-лена, непрерывна на отрезке
опреде-лена, непрерывна на отрезке  , дифференцируема на интер-вале
, дифференцируема на интер-вале  , то существует точка
, то существует точка  , в которой выпол-няется равенство
, в которой выпол-няется равенство
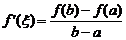 . (21)
. (21)
Геометрический смысл теоремы Лагранжа состоит в том, что для дифференцируемой функции, определенной на  , существует точка x, содержащаяся внутри интервала
, существует точка x, содержащаяся внутри интервала  , такая, что касательная к кривой
, такая, что касательная к кривой 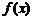 в этой точке параллельна секущей AB (рис. 9.4), что следует из равенства
в этой точке параллельна секущей AB (рис. 9.4), что следует из равенства  .
.

Рис. 9.4
Замечание. Теорему Лагранжа часто называют теоремой о среднем значении, а формулу (21) – формулой Лагранжа о конечных приращениях. Этому названию можно дать следующее объяснение.
Рассмотрим промежуток 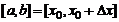 . Применим к нему теорему Лагранжа (при любом допустимом
. Применим к нему теорему Лагранжа (при любом допустимом  ), будем иметь точное равенство
), будем иметь точное равенство
 ,
,
где  ,
, 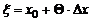 или
или
 .
.
Недостаток формулы Лагранжа заключается в том, что x неизвестно, так как неизвестно число Q. Тем не менее, формула конеч-ных приращений очень важна в теоретических исследованиях.
Теорема 9.6 (Кошú). Пусть функции  ,
,  определены, непрерывны на отрезке
определены, непрерывны на отрезке  и дифференцируемы на интервале
и дифференцируемы на интервале  , причем
, причем 
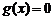 , тогда существует точка
, тогда существует точка  , в которой выполняется равенство
, в которой выполняется равенство
 .
.
Геометрический смысл теоремы Коши аналогичен теореме Лагранжа.
Правило Лопиталя
Пусть функции  ,
,  дифференцируемы и
дифференцируемы и  в некоторой окрестности точки
в некоторой окрестности точки 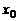 . Если
. Если  или
или  , тогда предел отношения этих функций равен пределу отношения их производных
, тогда предел отношения этих функций равен пределу отношения их производных

при условии, что существует  .
.
Замечание. Отметим, что правило Лопиталя применяется только в том случае, если имеет место неопределенное выражение вида  или
или  .
.
Например, вычислить предел, используя правило Лопиталя,  .
.
Формула Тейлора
Формула Тейлора


имеет большое теоретическое и практическое значение. В частности, с ее помощью можно вычислить приближенное значение функции 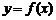 по известным значениям этой функции и ее n производных в точке
по известным значениям этой функции и ее n производных в точке  и оценивать точность этого вычисления.
и оценивать точность этого вычисления.
Для оценки погрешности формулы Тейлора важна форма записи остаточного члена  Распространенной является запись остаточного члена в форме Лагранжа:
Распространенной является запись остаточного члена в форме Лагранжа:
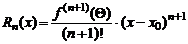 ,
,
где Q – произвольное число из интервала  .
.
Пример 9.12. Применяя формулу Тейлора с остаточным членом в форме Лагранжа, вычислить e 0,1 с точностью до 0,001.
Решение. Формула Тейлора с остаточным членом в форме Лагранжа для функции  при
при  имеет вид
имеет вид
 ,
,
 ,
,  .
.
Для любого значения х, находящегося в промежутке 0 < x < 1, имеем 1< ex <3, и, следовательно,  . Очевидно, условие
. Очевидно, условие  будет выполнено, если
будет выполнено, если  или
или  .
.
Вычисляя последовательно слагаемые, входящие в формулу Тейлора, одновременно имеем возможность видеть, достигнута ли требуемая точность d. Полагая d = 0,001 и х = 0,1, получаем, что заданная точность вычислений будет достигнута при 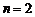 , тогда имеем:
, тогда имеем:
 .
.




 – дифференцируемые функции,
– дифференцируемые функции, 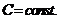
 ;
;

 ;
;
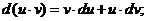
 ,
,  .
.
 функции
функции  тоже есть функция от x и называется производной 1-го порядка (1-й производной).
тоже есть функция от x и называется производной 1-го порядка (1-й производной). дифференцируемая, то ее производ-ная называется производной 2-го порядка (2-й производной) и обозначается
дифференцируемая, то ее производ-ная называется производной 2-го порядка (2-й производной) и обозначается  ,
,  или
или  .
. ,
,  или
или  .
. ,
,  .
. имеем:
имеем:  ;
;  ;
; 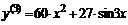 и т. д.
и т. д. .
. , то
, то 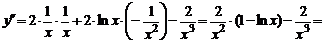
 .
. ,
,  ,
,  , функции
, функции 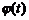 ,
,  дифференцируемые, по крайней мере, n -го порядка включительно,
дифференцируемые, по крайней мере, n -го порядка включительно,  ,
,  ,
,  , … вычисляются по формулам:
, … вычисляются по формулам:
 ,
,  и т. д.
и т. д. ,
,  имеем:
имеем: ;
;  .
. часто позволяет делать выводы о по-ведении на нем самой функции. Обоснованию этого заявления и посвящена оставшаяся часть пособия.
часто позволяет делать выводы о по-ведении на нем самой функции. Обоснованию этого заявления и посвящена оставшаяся часть пособия. определена и непрерывна на отрезке
определена и непрерывна на отрезке  , достигает наибольшего (наи-меньшего) значения в точке
, достигает наибольшего (наи-меньшего) значения в точке  и имеет в ней конечную производную, то производная функции в этой точке равна нулю, то есть
и имеет в ней конечную производную, то производная функции в этой точке равна нулю, то есть  .
. , то существует хотя бы одна точка
, то существует хотя бы одна точка  , производная функции в которой равна нулю, то есть
, производная функции в которой равна нулю, то есть  .
. , в которой выпол-няется равенство
, в которой выпол-няется равенство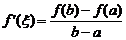 . (21)
. (21) в этой точке параллельна секущей AB (рис. 9.4), что следует из равенства
в этой точке параллельна секущей AB (рис. 9.4), что следует из равенства  .
.
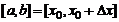 . Применим к нему теорему Лагранжа (при любом допустимом
. Применим к нему теорему Лагранжа (при любом допустимом  ), будем иметь точное равенство
), будем иметь точное равенство ,
, ,
, 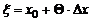 или
или .
. ,
,  определены, непрерывны на отрезке
определены, непрерывны на отрезке  и дифференцируемы на интервале
и дифференцируемы на интервале  , причем
, причем 
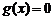 , тогда существует точка
, тогда существует точка  .
. дифференцируемы и
дифференцируемы и  в некоторой окрестности точки
в некоторой окрестности точки 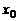 . Если
. Если  или
или  , тогда предел отношения этих функций равен пределу отношения их производных
, тогда предел отношения этих функций равен пределу отношения их производных
 .
. или
или  .
. .
.

 и оценивать точность этого вычисления.
и оценивать точность этого вычисления. Распространенной является запись остаточного члена в форме Лагранжа:
Распространенной является запись остаточного члена в форме Лагранжа: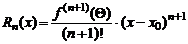 ,
, .
. при
при  имеет вид
имеет вид ,
, ,
,  . Очевидно, условие
. Очевидно, условие  будет выполнено, если
будет выполнено, если  или
или  .
.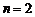 , тогда имеем:
, тогда имеем: .
.


