В практической деятельности каждому специалисту приходится иметь дело с разнообразными ситуациями, в которых нужно варьировать событиями. Во многих случаях эти ситуации связаны с решением комбинаторных задач.
Комбинаторика изучает комбинации, подчинённые определённым условиям, которые можно составить из элементов любой природы. Она основана на двух правилах: сложение и умножение.
Правило сложения: если некоторое событие А может произойти m раз, а событие В – n раз, то событие А или В может произойти m + n раз.
Правило умножения: если событие А произойдёт m раз, а событие В – n раз, то событие А и В произойдёт одновременно m  n раз.
n раз.
События совместные, если они могут в данном испытании произойти одновременно, и несовместные, если произойдёт только одно из этих событий.
Рассмотрим 3 типа комбинаторных формул (комбинаций): перестановки, сочетания, размещения.
1. Перестановки – такой тип комбинаций, который связан с нумерацией и перестановкой элементов.
Теорема 1. Число перестановок без повторений вычисляют по формуле: Рn = n  (n
(n  = 1
= 1  2
2  …
…  n).
n).
Теорема 2. Число перестановок с повторениями вычисляют по формуле:
Рn= (К1, К2,…,Кn) = 
2. Сочетание – такой тип комбинаций, который связан с выбором элементов.
Теорема 3. Число сочетаний без повторений вычисляют по формуле: Cnm= 
Теорема 4. Число сочетаний с повторениями вычисляют по формуле:  nm=
nm= 
3. Размещение – такой тип комбинаций, который связан с выбором элементов и с их перестановкой.
Теорема 5. Число размещений без повторений вычисляют по формуле: Anm= 
Теорема 6. Число размещений с повторениями вычисляют по формуле: 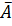 nm=
nm= 
5. Статистическое и геометрическое определения вероятности. Примеры.
Классическое определение вероятности применимо только для тех событий, которые могут появиться в результате испытания и обладают симметрией возможных исходов. Однако существует большой класс событий, вероятность которых нельзя вычислить с помощью классического определения. Эти события не являются равновозможными. В этом случае используют статистическое определение вероятности. Оно связано с понятием «относительная частота».
Относительная частота события А – это отношение числа опытов, в которых появилось событие А, к общему числу опытов: ω(A) = 
Большое количество экспериментов показало, что если опыты проводятся в одинаковых условиях, то относительная частота будет колебаться около какого-то числа. Это число можно считать вероятностью события.
Пример: английский учёный Пирсон произвёл 23000 бросаний монеты. Герб появился 11512 раз.
ω(A) =  = 0, 5005
= 0, 5005
Статистической вероятностью будем считать относительную частоту или число, близкое к ней: Р(А) = ω(A) = 
В отличие от классической вероятности, статистическая вероятность является опытной величиной. Классическая вычисляется ДО опыта, а статистическая – ПОСЛЕ.
Статистическая вероятность обладает определёнными свойствами:
1. рассматриваемые события должны быть исходами только тех событий, которые могут быть проведены неограниченное число раз в одних и тех же условиях;
2. события должны обладать свойством статистической устойчивости;
3. число испытаний, в которых появилось событие А, должно быть достаточно велико.
Геометрическая вероятность.
Чтобы преодолеть недостаток классического определения, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрическую вероятность.
Пусть на отрезок L брошена точка, которая может попасть с равной возможностью в любую точку отрезка, тогда вероятность того, что брошенная точка попадёт в отрезок l, будет вычисляться по формуле: Р(А) =  , где mes – мера (длина).
, где mes – мера (длина).
Если точка брошена в область G, то вероятность того, что она попадёт в область g, будет вычисляться по формуле: Р(А) =  =
=  , где mes – мера (площадь).
, где mes – мера (площадь).
Если точку бросить в пространство, то: Р(А) = 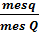 =
=  , где mes – мера (объём).
, где mes – мера (объём).
Геометрическая вероятность события А – это отношение меры благоприятной области к общей области: Р(А) = 
Пример: найти вероятность того, что точка, брошенная в круг, не попадёт в правильный шестиугольник, вписанный в круг.
Решение:
Р(А) =  =
=  =
=  0,33, 33%
0,33, 33%
Ответ: 33%.



 n раз.
n раз. (n
(n 

 nm=
nm= 

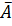 nm=
nm= 

 = 0, 5005
= 0, 5005 , где mes – мера (длина).
, где mes – мера (длина). =
=  , где mes – мера (площадь).
, где mes – мера (площадь).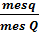 =
=  , где mes – мера (объём).
, где mes – мера (объём).
 =
=  =
=  0,33, 33%
0,33, 33%


