Предмет и задачи теории вероятностей. Понятие эксперимента, события и их классификация. Пространство элементарных событий.
Подавляющее большинство окружающих явлений содержит в себе элементы случайностей. Окружающий нас мир насыщен случайными событиями. Знание закономерностей, которым подчиняются случайные явления, позволяет предвидеть, как они будут протекать.Теория вероятностей не ставит перед собой задачу предсказать, произойдёт или нет какое-либо событие, но, если данное событие многократно наблюдается, то оно подчиняется определённым закономерностям, установлением которых и занимается Теория Вероятностей.
Предмет теории вероятностей – изучение вероятностных закономерных массовых случайных событий.
Первые работы, в которых зарождались основы ТВ, представляют собой попытку создания теории азартных игр (Кардано, Паскаль, Гюйгенс). Следующий этап развития ТВ связан с именами математиков: Бернулли, Лаплас, Пуассон. Её последующее развитие связано с русскими и советскими математиками: Чебышев, Ляпунов, Колмогоров, Марков.
Методы ТВ широко применяются в теории надёжности, теории массового обслуживания, теории планирования и управления.
Испытание – реализация определённого комплекса условий, которые могут воспроизводиться неограниченное число раз. Результат испытания – событие, которое обозначается А, В, С.
События достоверны, если они обязательно произойдут в данном испытании, обозначаются U.
Невозможное событие – событие, которое никогда не произойдёт в данном испытании, обозначается V.
Случайное событие – событие, которое в данном испытании может произойти или не произойти.
Конкретный результат испытания – элементарное событие.
Совокупность всех элементарных событий – пространство элементарных событий.
Сложноесобытие – подмножество пространства элементарных событий.
События независимые, если исход одного из них не влияет на исход других.
Два события противоположны, если исход одного из них противоречит наступлению другого.
Операции над событиями.
Сложение событий: событие С называется суммой событий А и В, если оно состоит из всех элементарных событий, входящих хотя бы в одно из событий А или В.
А + В = С (или)
Умножение событий: событие С называется произведением событий А и В, если оно состоит из всех элементарных событий, входящих и в А, и в В.
А  В = С (и)
В = С (и)
Разность событий: разность событий А без В – это такое событие С, состоящее из элементарных событий, входящих в А, но не входящих в В.
А \ В = С (без)
Геометрическая вероятность.
Чтобы преодолеть недостаток классического определения, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрическую вероятность.
Пусть на отрезок L брошена точка, которая может попасть с равной возможностью в любую точку отрезка, тогда вероятность того, что брошенная точка попадёт в отрезок l, будет вычисляться по формуле: Р(А) =  , где mes – мера (длина).
, где mes – мера (длина).
Если точка брошена в область G, то вероятность того, что она попадёт в область g, будет вычисляться по формуле: Р(А) =  =
=  , где mes – мера (площадь).
, где mes – мера (площадь).
Если точку бросить в пространство, то: Р(А) = 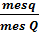 =
=  , где mes – мера (объём).
, где mes – мера (объём).
Геометрическая вероятность события А – это отношение меры благоприятной области к общей области: Р(А) = 
Пример: найти вероятность того, что точка, брошенная в круг, не попадёт в правильный шестиугольник, вписанный в круг.
Решение:
Р(А) =  =
=  =
=  0,33, 33%
0,33, 33%
Ответ: 33%.
Теоремы суммы вероятностей.
Т1: Вероятность суммы двух несовместных событий равна сумме их вероятности.
Р(А+В)=Р(А)+Р(В)
Т2: Вероятность суммы двух совместных событий вычисляют по формуле:
Р(А+В)=Р(А)+Р(В) – Р(А*В)
Зам.1: Р(А+В+С)=Р(А)+Р(В)+Р(С) – Р(А*В) – Р(А*С) – Р(В*С) + Р(А*В*С)
8. Вероятность наступления хотя бы одного события.
Зам.2: Для 4-х и более совместных событий предыдущие формулы(формулы сложения и произведения вероятностей) неудобны, необходимо применить Т3.
Т3: Вероятность наступления хотя бы одного из нескольких независимых событий вычисляется по формуле:
Р(А)=1 – q1*q2*…*qn, где q=1 – р.
Зам.3: Если вероятность независимых событий одинаковы, р1=р2=….=рn, то формула будет иметь вид: Р(А)= 1 – qn
Формула Пуассона.
Формула Бернулли требует громоздких расчётов при большом количестве испытаний. В этом случае применяют приближённую формулу Пуассона.
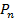 (m)=
(m)= 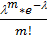 , n-велико, р-очень мала, l= n×p
, n-велико, р-очень мала, l= n×p
Случаные величины (СВ). Дискретные и непрерывные случайные величины. Ряд распределения дискретных случайных величин.
Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причём заранее неизвестно, какое именно.
Будем обозначать случайные величины заглавными буквами латинского алфавита: X, Y, Z, …, а их возможные значения соответственно: 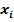 ,
,  , …
, …
Случайные величины подразделяют на 2 группы: дискретные и непрерывные.
Дискретная СВ — если она принимает отдельные изолированные возможные значения с определёнными вероятностями, т.е. эта величина, множество значений которой конечно(счётно).
Непрерывная СВ — если множество её значений целиком заполняет некоторый конечный или бесконечный промежуток.
Для задания ДСВ нужно знать её возможные значения и вероятности, с которыми принимаются эти значения.
Законом распределения ДСВ называется соответствие, устанавливающее связь между возможными значениями ДСВ и вероятностями этих значений. Оно может иметь вид таблицы, формулы или графика.
Таблица, в которой перечислены возможные значения ДСВ и соответствующие им вероятности, называется рядом распределения.
Заметим, что событие, заключающееся в том, что СВ примет одно из своих возможных значений, является достоверным. Поэтому:  =1
=1
Графически закон распределения ДСВ можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами ( ,
,  ).
).
рi
P DVWfu5O38PK+6d+qcntwH9NmNAesjiNHa6+vpscVqERT+gvDD76gQyFMZTixi6oTbcydRC0sZJL4 88WDHOWv1kWu//MX3wAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAA AAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAAL AAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQDaY6tfCgIAADsEAAAO AAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQA7fh8R2wAAAAcB AAAPAAAAAAAAAAAAAAAAAGQEAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAbAUAAAAA " strokecolor="black [3213]">
Распределение Стьюдента.
Рассмотрим 2 случайные величины:
Z – нормально распределенная величина;
U – распределенная по закону c2 .
Тогда величина T= 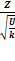 имеет распределение, называемое t-распределение или распределение Стьюдента с К- степенями свободы.
имеет распределение, называемое t-распределение или распределение Стьюдента с К- степенями свободы.
Замечание: с возрастанием числа степеней свободы распределение Стьюдента приближается к нормальному.
Неравенства Маркова.
Если случайная величина X принимает только неотрицательные значения и имеет математическое ожидание М(Х), то для любого положительного числа А верно неравенство:

 )
)
Неравенства Маркова применимо к любым неотрицательным случайным величинам.
Неравенство Чебышева.
Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо след. неравенство:
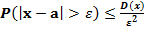 (1)
(1)
где а = М(x), ε >0 –достаточно малое число, но положительное число
Учитывая, что события по модулю |x-a| >  и |x-a| <
и |x-a| <  противоположны, неравенство Чебышева можно записать в другой форме:
противоположны, неравенство Чебышева можно записать в другой форме:
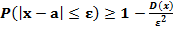 (2)
(2)
Неравенство Чебышева применимо для любых случайных величин. Неравенство Чебышева (1) устанавливает верхнюю границу, (2) – нижнюю границу вероятности рассматриваемого объекта.
Рассмотрим частные случаи для некоторых случайных величин:
1) Для случайных величин Х=m величина имеет биномиальное распределение, для неё математическое ожидание M(x)=np, а дисперсия D(x)=npq, тогда неравенство Чебышева будет иметь вид:  (3)
(3)
2) Для частоты  события в n независимых испытаниях, в каждой из которых событие появляется с вероятностью p, а=M(x)=p, а D(x)=
события в n независимых испытаниях, в каждой из которых событие появляется с вероятностью p, а=M(x)=p, а D(x)=  , тогда неравенство Чебышева примет вид:
, тогда неравенство Чебышева примет вид:
 (4)
(4)
Теорема Чебышева.
При большом числе n среднее арифметическое случайных величин X1, X2,.., Xn сколь угодно мало отличается от неслучайной величины  .
.
Теорема Чебышева имеет вид: 
Сущность теоремы Чебышева: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу, а именно к числу 
(или к числу а в частном случае). Иными словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.
Регрессионный анализ.
Регрессионный анализ — это статистический метод исследования зависимости случайной величины У от переменных (аргументов) хj (j = 1, 2,..., k), рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения хj.
Для проведения линейного регрессионного анализа зависимая переменная должна иметь интервальную (или порядковую) шкалу.
Бинарная логистическая регрессия выявляет зависимость дихотомической переменной от некой другой переменной, относящейся к любой шкале. Те же условия применения справедливы и для пробит-анализа.
Если зависимая переменная является категориальной c тремя и более категориями, то подходящим методом будет мультиномиальная логистическая регрессия.
Порядковую регрессию можно использовать, когда зависимые переменные относятся к порядковой шкале.
Нелинейные связи между переменными, которые относятся к интервальной шкале можно анализировать с помощью нелинейной регрессии.
Предмет и задачи теории вероятностей. Понятие эксперимента, события и их классификация. Пространство элементарных событий.
Подавляющее большинство окружающих явлений содержит в себе элементы случайностей. Окружающий нас мир насыщен случайными событиями. Знание закономерностей, которым подчиняются случайные явления, позволяет предвидеть, как они будут протекать.Теория вероятностей не ставит перед собой задачу предсказать, произойдёт или нет какое-либо событие, но, если данное событие многократно наблюдается, то оно подчиняется определённым закономерностям, установлением которых и занимается Теория Вероятностей.
Предмет теории вероятностей – изучение вероятностных закономерных массовых случайных событий.
Первые работы, в которых зарождались основы ТВ, представляют собой попытку создания теории азартных игр (Кардано, Паскаль, Гюйгенс). Следующий этап развития ТВ связан с именами математиков: Бернулли, Лаплас, Пуассон. Её последующее развитие связано с русскими и советскими математиками: Чебышев, Ляпунов, Колмогоров, Марков.
Методы ТВ широко применяются в теории надёжности, теории массового обслуживания, теории планирования и управления.
Испытание – реализация определённого комплекса условий, которые могут воспроизводиться неограниченное число раз. Результат испытания – событие, которое обозначается А, В, С.
События достоверны, если они обязательно произойдут в данном испытании, обозначаются U.
Невозможное событие – событие, которое никогда не произойдёт в данном испытании, обозначается V.
Случайное событие – событие, которое в данном испытании может произойти или не произойти.
Конкретный результат испытания – элементарное событие.
Совокупность всех элементарных событий – пространство элементарных событий.
Сложноесобытие – подмножество пространства элементарных событий.
События независимые, если исход одного из них не влияет на исход других.
Два события противоположны, если исход одного из них противоречит наступлению другого.
Операции над событиями.
Сложение событий: событие С называется суммой событий А и В, если оно состоит из всех элементарных событий, входящих хотя бы в одно из событий А или В.
А + В = С (или)
Умножение событий: событие С называется произведением событий А и В, если оно состоит из всех элементарных событий, входящих и в А, и в В.
А  В = С (и)
В = С (и)
Разность событий: разность событий А без В – это такое событие С, состоящее из элементарных событий, входящих в А, но не входящих в В.
А \ В = С (без)



 В = С (и)
В = С (и) , где mes – мера (длина).
, где mes – мера (длина). =
=  , где mes – мера (площадь).
, где mes – мера (площадь).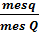 =
=  , где mes – мера (объём).
, где mes – мера (объём).
 =
=  =
=  0,33, 33%
0,33, 33%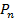 (m)=
(m)= 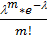 , n-велико, р-очень мала, l= n×p
, n-велико, р-очень мала, l= n×p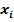 ,
,  , …
, …








 =1
=1  ,
,  ).
).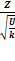 имеет распределение, называемое t-распределение или распределение Стьюдента с К- степенями свободы.
имеет распределение, называемое t-распределение или распределение Стьюдента с К- степенями свободы.
 )
)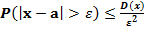 (1)
(1) и |x-a| <
и |x-a| < 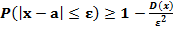 (2)
(2) (3)
(3) события в n независимых испытаниях, в каждой из которых событие появляется с вероятностью p, а=M(x)=p, а D(x)=
события в n независимых испытаниях, в каждой из которых событие появляется с вероятностью p, а=M(x)=p, а D(x)=  , тогда неравенство Чебышева примет вид:
, тогда неравенство Чебышева примет вид:  (4)
(4)




