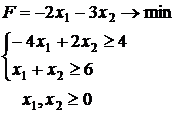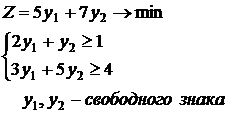S: Количество двойственных переменных равно

+: количеству ограничений исходной задачи

-: количеству переменных исходной задачи

-: количеству ограничений двойственной задачи

-: рангу системы ограничений исходной задачи

 

I:

S: Величина двойственной оценки численно равна:

+: изменению целевой функции при изменении соответствующего свободного члена ограничений на единицу

-: наибольшему возможному изменению свободного члена ограничений

-: наименьшему изменению коэффициентов целевой функции

-: наибольшему изменению коэффициентов целевой функции

I:

S: Смысл двойственных оценок в линейном программировании состоит:

-: в определении размеров прибыли или убытков в процессе производства

-: в оценке целесообразности торгово-экономических мероприятий

+: в определении сравнительной дефицитности различных видов ресурсов в отношении принятого в задаче показателя эффективности

-: в определении спроса и предложения в процессе производства

I:

S: Двойственные оценки показывают приращение целевой функции задачи математического программирования, вызванное:

-: фиксированным изменением свободного члена соответствующего ограничения

-: достаточно большим изменением свободного члена

+: малым изменением свободного члена

+: малым изменением коэффициентов целевой функции

I:

S: Условия дополняющей нежесткости экономически означают (для задачи оптимального использования ресурсов), в частности, что если в некотором оптимальном плане двойственных оценок его i-ая компонента строго больше нуля, то:

+: в оптимальном плане производства расход соответствующего ресурса равен его запасу

-: другие компоненты равны нулю

-: в оптимальном плане производства расход соответствующего ресурса меньше его запаса

-: другие компоненты меньше нуля

I:

S: Если переменная х_j исходной ЗЛП на максимум может принимать только лишь положительные значения, то j-ое ограничение двойственной задачи является:

-: неравенством вида «≤»

-: равенством

+: неравенством вида «≥»

-: не существенным

I:

S: Неизвестные в паре взаимно-двойственных симметрических ЗЛП:

-: имеют противоположные знаки

+: неотрицательны

-: положительны

-: свободного знака

I:

S: Переменные задачи, двойственной к канонической ЗЛП:

-: отрицательны

-: положительны

+: могут быть и положительными и отрицательными

-: равны нулю

I:

S: Коэффициентами при неизвестных в целевой функции двойственной задачи являются:

-: коэффициенты целевой функции исходной задачи с противоположными знаками

+: свободные члены системы ограничений исходной задачи

-: свободные члены системы ограничений исходной задачи, умноженные на -1

-: коэффициенты целевой функции исходной задачи

I:

S: Правыми частями в системе ограничений двойственной задачи являются:

-: нули

-: коэффициенты при неизвестных в целевой функции исходной задачи с противоположными знаками

-: правые части системы ограничений прямой задачи

+: коэффициенты при неизвестных в целевой функции исходной задачи

I:

S: Если переменная х_j может принимать как положительные, так и отрицательные значения, то j-ое ограничение двойственной задачи представляет собой:

+: уравнение

-: неравенство вида «>»

-: неравенство вида «<»

-: неравенство вида «»

I:

S: Если i-е ограничение исходной задачи ЛП на максимум является неравенством, то i-я переменная двойственной задачи:

-: y_i = 0

+: y_i ≥ 0

-: y_i < 0

-: y_i < 1

I:

S: Число переменных в двойственной задаче равно числу

+: переменных в исходной задаче

-: отличных от нуля правых частей исходной задачи

-: ограничений исходной задачи

-: ненулевых коэффициентов целевой функции исходной задачи

I:

S: Матрицы коэффициентов системы ограничений двойственной задачи и системы ограничений исходной задачи

-: совпадают

+: являются транспонированными друг к другу

-: являются взаимно обратными

-: вырожденные

I:

S: Если i-ое ограничение исходной задачи ЛП является равенством, то i-я переменная двойственной задачи:

-: y_i > 0

+: y_i - свободного знака

-: y_i = 0

-: y_i < 0

I:

S: Если каноническая ЗЛП имеет оптимальный план Х*, то оптимальным планом двойственной задачи (С_б – вектор-строка из коэффициентов целевой функции исходной задачи; Р – матрица, составленная из компонент векторов базиса) является план У*, равный:

+: У* = С_б · Р^-1

-: У* = С_б · Х*

-: У* = С_б · Р

-: У* = Х*· Р

 

I:

S: Компоненты оптимального плана двойственной задачи ЛП (если двойственная пара симметричная) находятся в последней симплексной таблице исходной задачи:

-: в столбце свободных членов

-: в индексной строке в столбцах, соответствующих основным переменным

+: в индексной строке в столбцах, соответствующих дополнительным переменным

-: в столбце коэффициентов целевой функции

I:

S: Исходная ЗЛП имеет вид:

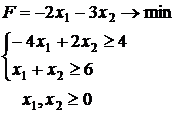
Тогда двойственная задача запишется в виде:

+:

-:

-:

I:

S: Исходная ЗЛП имеет вид:

Тогда двойственная задача запишется в виде:

-:

-:

+:

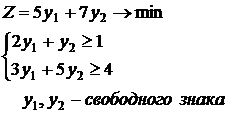
I:

S: Двойственный симплексный метод целесообразно применять при решении ЗЛП:

-: если все свободные члены положительны

+: свободные члены системы ограничений, которой могут быть любыми числами

-: с целевой функцией, имеющей неотрицательные коэффициенты и только на максимум

-: с целевой функцией, имеющей отрицательные коэффициенты

I:

S: Условно-оптимальным планом (или псевдопланом) ЗЛП на максимум называется:

-: любое базисное решение

-: любой опорный план, для которого среди оценок свободных переменных нет нулевых

+: любое возможное решение, для которого все оценки свободных переменных неотрицательны

-: приближённое решение

I:

S: Термин "теневая цена" означает

-: изменение плана при изменении ресурса на единицу

+: изменение значения целевой функции при изменении ресурса на единицу -: предельно допустимое значение ресурса

-: изменение значения целевой функции при изменении одного из ее коэффициентов

I:

S: "Теневая цена" имеет смысл для ресурсов

-: с ограничениями сверху

-: с ограничениями снизу

+: несвязанных

-: связанных

I:

S: Если "теневая цена" ресурса превосходит рыночную цену, то выгодно +: приобретать этот ресурс

-: продавать этот ресурс

-: ничего не делать

-: изменить "теневую цену"

I:

S: Если "теневая цена" ресурса меньше рыночной цены, то выгодно

-: приобретать этот ресурс

+: продавать этот ресурс

-: ничего не делать

-: изменить "теневую цену"

I:

S: Если "теневая цена" ресурса равна рыночной цене, то выгодно

-: приобретать этот ресурс

-: продавать этот ресурс

+: ничего не делать

-: изменить "теневую цену"

I:

S: Критические границы ресурсов соответствуют

-: границам устойчивости статуса ограничений при изменении коэффициентов целевой функции

-: границам устойчивости статуса ограничений при изменении коэффициентов их левых частей

+: границам устойчивости статуса ограничений при изменении их правых частей

-: допустимым уменьшению и увеличению ресурса

I:

S: Допустимое увеличение ресурса позволяет изменить статус ограничений

-: да

+: нет

-: да, если ограничения - строгие неравенства

-: да, если ограничения – равенства

I:

S: Допустимое уменьшение ресурса позволяет изменить "теневую цену"

-: да

+: нет

-: да, если теневая цена положительна

-: да, если теневая цена отрицательна

I:

S: Критические границы цен соответствуют

+: границам устойчивости оптимального плана при изменении коэффициентов целевой функции

-: границам устойчивости оптимального плана при изменении коэффициентов левых частей ограничений

-: границам устойчивости оптимального плана при изменении правых частей ограничений

I:

S: Допустимое увеличение цен позволяет изменить статус ограничений

-: да

+: нет

-: необходимы дополнительные сведения

I:

S: Допустимое уменьшение цен позволяет изменить "теневую цену"

-: да

+: нет

-: необходимы дополнительные сведения.