-: одна переменная
+: две переменные
-: три переменные
-: четыре переменные
I:
S: Если область допустимых решений задачи ЛП состоит из единственной точки, то целевая функция в ней
-: принимает постоянное отрицательное значение
-: принимает нулевое значение
-: не ограничена
+: достигает одновременно и максимального и минимального значений
I:
S: При решении ЗЛП на  линия уровня при движении в направлении градиента
линия уровня при движении в направлении градиента  выходит из множества допустимых планов в точке пересечения прямых
выходит из множества допустимых планов в точке пересечения прямых  и
и  . Тогда оптимальным будет план
. Тогда оптимальным будет план
-: (3,1)
+: (1,3)
-: (1,2)
-: (2,0)
I:
S: При решении ЗЛП на  линия уровня при движении в направлении градиента
линия уровня при движении в направлении градиента  выходит из множества допустимых планов в точке пересечения прямых
выходит из множества допустимых планов в точке пересечения прямых  и
и  . Тогда оптимальным будет план
. Тогда оптимальным будет план
-: (8,6)
-: (6,8)
-: (5,4)
+: (4,5)
I:
S: При решении ЗЛП на  линия уровня при движении в направлении градиента
линия уровня при движении в направлении градиента  выходит из множества допустимых планов в точке пересечения прямых
выходит из множества допустимых планов в точке пересечения прямых  и
и  . Тогда оптимальным будет план
. Тогда оптимальным будет план
-: (4,1)
-: (3,2)
+: (2,3)
-: (1,4)
I:
S: Решением ЗЛП на  является точка.
является точка.

-: F
-: E
-: D
-: B
+: A
I:
S: Решением ЗЛП на  является точка.
является точка.

-: F
+: E
-: D
-: B
-: A
I:
S: Решением ЗЛП на  является точка.
является точка.

-: F
-: E
-: D
+: B
-: A
I:
S: Решением ЗЛП на  является точка.
является точка.

+: F
-: E
-: D
-: B
-: A
I:
S: Решением ЗЛП на  является точка.
является точка.

-: F
-: E
+: D
-: B
-: A
I:
S: Область допустимых решений задачи линейного программирования имеет вид
*2

Тогда максимальное значение функции  равно
равно
-: 26
-: 28
+: 30
-: 24
I:
S: Область допустимых решений задачи линейного программирования имеет вид

Тогда максимальное значение функции  равно
равно
-: 26
-: 28
+: 30
-: 24
I:
S: Область допустимых решений задачи линейного программирования имеет вид

Тогда максимальное значение функции  равно
равно
-: 26
-: 32
+: 30
-: 24
I:
S: Область допустимых решений задачи линейного программирования имеет вид

Тогда максимальное значение функции  равно
равно
-: 11
-: 14
-: 10
+: 13
I:
S: В случае решения задачи ЛП на минимум линию уровня Z = Z0 перемещают:
-: в градиентном направлении
+: в антиградиентом направлении
-: в произвольном направлении
-: в направлении, перпендикулярном вектору – градиенту
I:
S: Область допустимых планов это
-: линия соответствующая конкретному значению целевой функции
+: область, образуемая пресечением всех полуплоскостей, соответствующих отдельным неравенствам системы;
-: область, образуемая пересечением осей координат и линии соответствующей конкретному значению целевой функции
-: любая линия параллельная оси абсцисс
I:
S: Линия уровня целевой функции это
+: линия, соответствующая конкретному значению целевой функции
-: любая линия, параллельная оси абсцисс
-: любая линия, перпендикулярная оси абсцисс
-: любая линия, параллельная оси ординат
I:
S: Вектор-градиент целевой функции проходит
+: через начало координат
-: перпендикулярно оси абсцисс
-: перпендикулярно оси ординат
-: через точку максимума
I:
S: Вектор-градиент целевой функции проходит
+: через точку с координатами  ,где
,где  -коэффициенты целевой функции
-коэффициенты целевой функции
-: параллельно оси абсцисс
-: перпендикулярно оси ординат
-: через точку минимума
I:
S: Оптимуму задачи соответствует
-: любое положение линии уровня в области допустимых планов
-: положение линии уровня, проходящей через точку  ,где
,где  - коэффициенты целевой функции
- коэффициенты целевой функции
-: любое положение линии уровня вне области допустимых планов
+: крайнее положение линии уровня в области допустимых планов
I:
S: Если область допустимых планов пуста, то задача линейного программирования
-: имеет единственное решение
+: не имеет решения
-: имеет несколько решений
-: имеет бесконечно много решений
I:
S: Если область допустимых планов не пуста и не ограничена, то задача линейного программирования
-: всегда имеет решение
+: не всегда имеет решение
-: не имеет решения
-: имеет бесконечно много решений
I:
S: Если область допустимых планов не пуста и ограничена, то задача линейного программирования
+: имеет решение
-: не имеет решения
-: имеет несколько решений
-: имеет бесконечно много решений
I:
S: Симплекс-метод предназначен для решения
-: системы нелинейных уравнений
+: задачи линейного программирования
-: системы трансцендентных уравнений
- задачи динамического программирования
I:
S: Если область допустимых планов не пуста и ограничена, то допустимый план находится
-: на границе области допустимых планов
-: внутри границ области допустимых планов
+: в любой точке (внутри и на границе области допустимых планов)
-: вне границ области допустимых планов
I:
S: Область допустимых решений задачи линейного программирования имеет вид

Тогда максимальное значение функции  равно
равно
-: 11
+: 13
-: 10
-: 15
I:
S: Область допустимых решений задачи линейного программирования имеет вид

Тогда минимальное значение функции  равно
равно
-: 1
-: 3
+: 2
-: 0
I:
S: Если область допустимых планов не пуста и ограничена, то оптимальный план находится
-: вне границ области допустимых планов
+: на границе области допустимых планов
-: внутри границ области допустимых планов
-: в любой точке (внутри и на границе области допустимых планов)
I:
S: Если область допустимых планов не пуста и ограничена и существует единственный оптимальный план, то он находится
-: на одной из границ области допустимых планов
+: в одной из вершин области допустимых планов
-: внутри границ области допустимых планов
-: вне границ области допустимых планов
85. Если область допустимых планов не пуста и ограничена и существует множество оптимальных планов, то любой из них находится
-: вне границ области допустимых планов
+: на одной из границ области допустимых планов
-: в одной из вершин области допустимых планов
-: внутри границ области допустимых планов
I:
S: Связанным называется ограничение, определяемое
-: строгим неравенством
-: нестрогим неравенством
+: равенством
I:
S: Целевая функция:  , ограничения:
, ограничения:  <=3;
<=3;  <=2;
<=2;  >=0;
>=0;  >=0. Координаты плана, максимизирующего
>=0. Координаты плана, максимизирующего 
-: 
-: 
+: 
-: 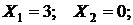
I:
S: Целевая функция:  , ограничения:
, ограничения:  <=2;
<=2;  <=3;
<=3;  >=0;
>=0;  >=0. Координаты плана, максимизирующего
>=0. Координаты плана, максимизирующего 
+: 
-: 
-: 
-: 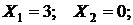
I:
S: Целевая функция:  , ограничения:
, ограничения: 
 <=3;
<=3;  <=3;
<=3;  >=0;
>=0;  >=0. Координаты плана, максимизирующего
>=0. Координаты плана, максимизирующего 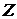
-: 
-: 
-: 
+: 
I:
S: Целевая функция: 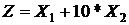 , ограничения:
, ограничения: 
 <=3;
<=3;  <=3;
<=3;  >=0;
>=0;  >=0. Координаты плана, максимизирующего
>=0. Координаты плана, максимизирующего 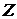
-: 
+: 
-: 
-: 
I:
S: Целевая функция:  , ограничения:
, ограничения: 
 <=3;
<=3;  <=3;
<=3;  >=0;
>=0;  >=0. Координаты плана, максимизирующего
>=0. Координаты плана, максимизирующего 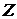
-: 
-: 
-: 
+: имеется множество оптимальных планов



 линия уровня при движении в направлении градиента
линия уровня при движении в направлении градиента  выходит из множества допустимых планов в точке пересечения прямых
выходит из множества допустимых планов в точке пересечения прямых  и
и  . Тогда оптимальным будет план
. Тогда оптимальным будет план и
и  . Тогда оптимальным будет план
. Тогда оптимальным будет план и
и  . Тогда оптимальным будет план
. Тогда оптимальным будет план
 является точка.
является точка.




 равно
равно

 равно
равно
 равно
равно ,где
,где 
 равно
равно , ограничения:
, ограничения:  <=3;
<=3;  <=2;
<=2; 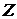



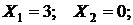
 , ограничения:
, ограничения: 



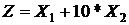 , ограничения:
, ограничения:  , ограничения:
, ограничения: 


