

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Дисциплины:
|
из
5.00
|
Заказать работу |
I:
S: Для решения задачи ЛП симплексным методом ее нужно представить:
-: в стандартной форме
-: в матричной форме
+: в канонической форме
-: в векторной форме
I:
S: Задачу максимизации можно заменить задачей минимизации, воспользовавшись соотношением для целевой функции F
-: max F = min (- F)
+: max F = - min F
-: max F = - min (-F)
I:
S: Опорным планом основной задачи ЛП называется:
+: базисный план с неотрицательными компонентами
-: допустимый план с положительными компонентами
-: любой базисный план
I:
S: Ранг матрицы системы ограничений ЗЛП с 5 переменными равен 3. Количество свободных переменных, содержащихся в выражении для общего решения системы ограничений, равно
-: 1
+: 2
-: 3
-: 4
I:
S: Ранг матрицы системы ограничений ЗЛП с 5 переменными равен 3. Количество базисных переменных, содержащихся в выражении для общего решения системы ограничений, равно
-: 1
-: 2
+: 3
-: 4
I:
S: При решении задачи на  рассматриваемый план ЗЛП будет оптимальным, если значения оценок
рассматриваемый план ЗЛП будет оптимальным, если значения оценок  в симплекс-таблице являются
в симплекс-таблице являются
+: неотрицательными
-: неположительными
-: отрицательными
-: положительными
I:
S: При решении задачи на  рассматриваемый план ЗЛП будет оптимальным, если значения оценок
рассматриваемый план ЗЛП будет оптимальным, если значения оценок  в симплекс-таблице являются
в симплекс-таблице являются
-: неотрицательными
+: неположительными
-: отрицательными
-: положительными
I:
S:Число дополнительных переменных, которые вводятся при решении симплекс-
методом ЗЛП с системой ограничений

равно
-: 4
-: 3
+:2
-: 1
I:
S:Число дополнительных переменных, которые вводятся при решении симплекс-
методом ЗЛП с системой ограничений

равно
-: 4
+: 3
-:2
-: 1
I:
S: В процессе решения симплекс-методом ЗЛП на  получено:
получено:
 . Тогда в базис нужно ввести переменную
. Тогда в базис нужно ввести переменную
-: никакую
-: 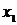
-: 
+: 
I:
S: В процессе решения симплекс-методом ЗЛП на  получено:
получено:
 . Тогда в базис нужно ввести переменную
. Тогда в базис нужно ввести переменную
-: никакую
+: 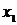
-: 
-: 
I:
S: В процессе решения симплекс-методом ЗЛП на  получено:
получено:
 . Тогда в базис нужно ввести переменную
. Тогда в базис нужно ввести переменную
-: никакую
-: 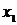
-: 
+: 
I:
S: Общее решение системы ограничений при оптимальном плане ЗЛП, полученное симплекс-методом, имеет вид  . Тогда оптимальным планом ЗЛП будет
. Тогда оптимальным планом ЗЛП будет
-: (5;1;2;0;0)
+: (0;5;1;0;2)
-: (5;0;1;0;2)
-: (5;1;0;0;0)
I:
S: Общее решение системы ограничений при оптимальном плане ЗЛП, полученное симплекс-методом, имеет вид  . Тогда оптимальным планом ЗЛП будет
. Тогда оптимальным планом ЗЛП будет
-: (7;5;2;0;0)
-: (7;0;0;5;2)
+: (7;0;0;0;2)
-: (7;2;0;0;0)
I:
S: Симплекс-методом найден оптимальный план х* = (1; 0; 6; 0; 2) для ЗЛП с целевой функцией 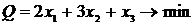 . Наименьшее значение целевой функции в этой ЗЛП равно
. Наименьшее значение целевой функции в этой ЗЛП равно
+: 8
-: 15
-: 10
-: 0
I:
S: Симплекс-методом найден оптимальный план х* = (2; 0; 5; 4; 0) для ЗЛП с целевой функцией  . Наибольшее значение целевой функции в этой ЗЛП равно
. Наибольшее значение целевой функции в этой ЗЛП равно
-: 20
-: 18
-: 19
+: 17
I:
S: По определению опорного плана (n – число переменных задачи ЛП; m – число линейно-независимых ограничений) число его положительных компонент:
-: равно n-1
-: больше m
-: равно n
+: не больше m
I:
S: Опорный план (m – число ограничений задачи ЛП) называется невырожденным, если он:
+: содержит ровно m положительных компонент
-: не содержит отрицательных компонент
-: содержит нулевые компоненты
-: не содержит нулевых компонент
I:
S: Пусть х1, х2, …, хn – произвольные точки евклидова пространства En. Выпуклой линейной комбинацией этих точек называется:
-: сумма х1 + х2 + … + хn
-: произведение х1 ∙ х2 ∙ … ∙ хn
+: сумма α1 · х1 + α2 · х2 + … + αn · хn, где αi – произвольные неотрицательные числа, сумма которых равна 1
-: квадратичная форма от этих точек
I:
S: Множество называется выпуклым, если оно содержит
-: все свои граничные точки
+: содержит вместе с любыми двумя своими точками и их произвольную выпуклую линейную комбинацию
-: все свои предельные точки
-: содержит вместе с любыми двумя своими точками и их какую-то выпуклую линейную комбинацию
I:
S: Точка Х выпуклого множества называется угловой (или крайней), если она
+: не может быть представлена в виде выпуклой линейной комбинации каких-нибудь двух других различных точек данного множества
-: может быть представлена в виде выпуклой линейной комбинации других точек данного множества
-: является граничной точкой данного множества
-: является предельной точкой данного множества
I:
S: Множество планов основной задачи ЛП является:
-: замкнутым и ограниченным
-: не ограниченным сверху
+: выпуклым, если оно не пусто
-: не ограниченным снизу
I:
S: Если основная задача ЛП имеет оптимальный план, то целевая функция достигает экстремального значения:
+: хотя бы в одной из вершин многогранника решений
-: в любой угловой точке многогранника решений
-: во внутренней точке многогранника решений
-: в любой граничной точке
I:
S: Если целевая функция задачи ЛП достигает экстремального значения более чем в одной вершине, то она достигает того же значения:
-: в любой граничной точке
+: в любой точке, являющейся их выпуклой линейной комбинацией
-: в любой другой вершине
-: во внутренней точке многогранника решений
I:
S: Для того чтобы каноническая задача ЛП имела решение необходимо, чтобы:
-: ранг системы ограничений был больше числа неизвестных (r > n)
-: уравнения системы ограничений были линейно зависимыми
+: ранг системы ограничений был не больше числа неизвестных (r  n)
n)
-: среди правых частей ограничений не было нулей
I:
S: Если допустимый план канонической задачи ЛП с m ограничениями имеет m положительных компонент, то он:
+: соответствует угловой (крайней) точке
-: является оптимальным
-: не является опорным
-: не является оптимальным
I:
S: Если система ограничений канонической задачи ЛП представлена в векторной форме и система векторов А1,А2,…,Аn содержит m линейно независимых векторов А1, А2, ….., Аm, то допустимый план Х = (х1, х2, …, хm, 0, …, 0) является:
+: угловой точкой многогранника планов
-: оптимальным планом
-: внутренней точкой многогранника планов
-: не является оптимальным
I:
S: Если Х – угловая точка многогранника планов, то те векторы Аj в системе ограничений канонической задачи в векторной форме, которые соответствуют положительным координатам вектора Х, образуют:
-: линейно зависимую систему
+: линейно независимую систему
-: ортогональную систему
-: оптимальный план
I:
S: Если допустимый план Х задачи ЛП с m ограничениями имеет m положительных координат, а все остальные равны нулю, то это:
+: опорный невырожденный план
-: оптимальный план
-: вырожденный план
I:
S: Если у допустимого плана Х задачи ЛП с m ограничениями число положительных компонент меньше m, а все остальные равны нулю, то такой план называется:
-: опорным невырожденным
+: опорным вырожденным
-: оптимальным
I:
S: Общая идея симплексного метода состоит:
-: в последовательном переборе всех вершин многогранника решений и выборе лучшей по целевой функции вершины
+: в рациональном переборе вершин, при котором от данной вершины переходят к смежной по ребру лучшей, от нее к еще лучшей и т.д.
-: в нахождении всех допустимых планов задачи ЛП и выборе наилучшего из них
I:
S: Если каждое ограничение ЗЛП в каноническом виде содержит переменную, входящую в левую часть с коэффициентом 1, а во все остальные с коэффициентом 0, то система ограничений представлена:
-: в развернутом виде
+: в предпочтительном виде
-: в допустимом виде
-: в сокращённом виде
I:
S: Основная теорема линейного программирования состоит в следующем:
-: решение ЗЛП находится внутри области допустимых решений
-: ЗЛП всегда имеет решение и оно находится на границе области допустимых решений
+: если ЗЛП имеет решение, то оно находится в одной из вершин многогранника решений
-: решение ЗЛП находится вне области допустимых решений
I:
S: Пусть система ограничений ЗЛП имеет предпочтительный вид. Тогда опорное решение задачи можно получить следующим образом:
+: все свободные переменные нужно приравнять нулю, тогда базисные переменные будут равны свободным членам
-: все базисные переменные приравнять нулю, тогда свободные переменные будут равны правым частям ограничений
-: базисные переменные приравнять коэффициентам целевой функции, а свободные переменные – правым частям
-: все свободные переменные нужно приравнять нулю, тогда базисные переменные будут равны коэффициентам целевой функции
I:
S: Mинимальное значение целевой функции  ЗЛП с оптимальным планом
ЗЛП с оптимальным планом  равно:
равно:
-: 3
+: 2
-: 5
-: 7
I:
S: Если система ограничений ЗЛП задана в форме:  , то начальный опорный план имеет вид:
, то начальный опорный план имеет вид:
+: Х = (0, 0, …., 0, b1, b2, …., bm)
-: Х = (b1, b2, …., bm, 0, 0, …., 0)
-: Х = (0, b 1, 0, b2, ….., 0, bm)
-: Х = (c1, c2, …., cm, 0, 0, …., 0)
I:
S: Начальный опорный план задачи ЛП

может иметь вид:
-: X =(0,10,50,0,10)
+: X =(0,10,80,32,0)
-: X =(10,0,32,0,80)
-: X =(0,2,4,0,1)
I:
S: Начальный опорный план задачи ЛП
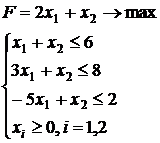
может иметь вид:
-: X =(0,8,0,0,2)
-: X =(0,1,8,2,6)
+: X =(0,0,6,8,2)
-: X =(2,1,0,0,2)
I:
S: Mаксимальное значение целевой функции  ЗЛП с оптимальным планом
ЗЛП с оптимальным планом 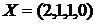 равно:
равно:
+: 11
-: 19
-: 15
-: 12
I:
S: Искусственный базис вводится для канонической ЗЛП в случае, если:
-: все ограничения имеют предпочтительный вид
-: правые части ограничений положительны и среди коэффициентов целевой функции нет отрицательных
+: не все ограничения имеют предпочтительный вид
-: среди правых частей есть отрицательные
I:
S: Для введения искусственного базиса при решении ЗЛП нужно:
+: к левым частям ограничений – равенств, не имеющих предпочтительного вида, добавить искусственные переменные
-: левые и правые части ограничений умножить на – 1
-: коэффициенты целевой функции умножить на – 1
+: к правым частям ограничений – равенств, не имеющих предпочтительного вида, добавить искусственные переменные
I:
S: Искусственные переменные вводят в целевую функцию ЗЛП на максимум с коэффициентами:
-: 0
+: – М, где М – большое положительное число
-: М, где М – большое положительное число
-: 1
I:
S: М –задача или расширенная задача, соответствующая исходной ЗЛП:
+: всегда имеет предпочтительный вид
-: не имеет предпочтительного вида
-: имеет оптимальный план
-: не имеет опорного плана
I:
S: Если в результате применения симплексного метода к расширенной задаче получен оптимальный план, в котором все искусственные переменные равны нулю, то:
-: исходная ЗЛП не имеет решения
+: первые n компонент дают оптимальный план исходной задачи
-: последние m компонент дают решение исходной ЗЛП
-: первые m компонент дают оптимальный план исходной задачи
I:
S: Если в оптимальном плане М –задачи хотя бы одна из искусственных переменных отлична от нуля, то исходная ЗЛП:
-: имеет допустимый план
-: имеет оптимальный план
+: не имеет допустимых планов
-: имеет опорный план
I:
S: Искусственные переменные вводят в целевую функцию ЗЛП на минимум с коэффициентами:
+: М, где М – большое положительное число
-: – М, где М – большое положительное число
-: 1
-: 0
I:
S: Если ЗЛП решается на максимум и для некоторого опорного плана все оценки свободных переменных неотрицательны, то такой план:
-: не оптимален
-: недопустимый
+: оптимален
-: вырожденный
I:
S: Симплексная таблица очередного шага решения ЗЛП на максимум имеет вид
 I
I
| Базис |

|

|

|

| -1

|

| -1

|

| -1 | 3/2 | 1/2 | -1/2 | ||||

| 11/2 | 3/2 | -1/2 | |||||

| 7/2 | 1/2 | 1/2 | |||||
  
| 
| 
| 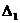
| 
| 
| 
| 
|
Элементы индексной (оценочной) строки равны:
-: 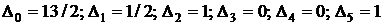
-: 
+: 
-: 
I:
S: Если ЗЛП решается на минимум и для некоторого опорного плана все оценки свободных переменных неположительные, то такой план:
-: не допустимый
+: оптимальный
-: неоптимальный
-: вырожденный
I:
S: Симплексная таблица очередного шага решения ЗЛП на максимум имеет вид
 I
I
| Базис |

|

|

|

|

|

|

|

| 1/2 | 1/2 | ||||||

| 1/2 | -1/2 | ||||||

| 3/2 | -1/2 | ||||||
  
| 
| -1 |
Разрешающим является элемент:
-: 1/2, стоящий на пересечении 1-й строки и столбца 
-: 3/2, стоящий на пересечении 3-й строки и столбца 
+: элемент 1/2, стоящий на пересечении 2-й строки и столбца 
-: -1/2, стоящий на пересечении 2-й строки и столбца 
I:
S: Симплексная таблица, содержащая оптимальное решение ЗЛП на максимум имеет вид
 i
i
| Базис |

|

|

|

|

|

|

|

| -1 | |||||||

| -1 | |||||||

| -3 | |||||||
  
| 
|
Тогда оптимальный план запишется в виде:
-: 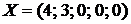
-: 
+: 
-: 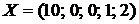
I:
S: Разрешающим столбцом в симплексной таблице ЗЛП на максимум называется вектор-столбец:
-: свободных членов
-: коэффициентов целевой функции
+: с минимальной отрицательной оценкой
-: с минимальной положительной оценкой
I:
S: Разрешающим столбцом в симплексной таблице ЗЛП на минимум является вектор-столбец:
-: коэффициентов при первой базисной переменной
+: с максимальной положительной оценкой
-: свободных членов
-: с минимальной положительной оценкой
I:
S: Разрешающим в симплексной таблице является:
-: любой элемент оценочной строки
-: любой элемент разрешающего столбца
+: элемент, стоящий на пересечении разрешающего столбца и разрешающей строки
-: элемент, стоящий на пересечении разрешающего столбца и оценочной строки
I:
S: На практике, в случае решения ЗЛП на максимум, число шагов, как правило, уменьшается, если разрешающий столбец (∆j – оценка j-й свободной переменной) выбрать по правилу:
-: max ∆j, ∆j < 0
+: max | ∆j |, ∆j < 0
-: max | ∆j |, ∆j  0
0
-: max | ∆j |, ∆j  0
0
I:
S: Разрешающую строку при решении ЗЛП симплексным методом выбирают:
-: по наименьшему отношению элементов столбца свободных членов к элементам разрешающего столбца
-: по наибольшему отношению элементов столбца свободных членов к отрицательным элементам разрешающего столбца
+: по наименьшему отношению элементов столбца свободных членов к соответствующим положительным элементам разрешающего столбца
-: по наибольшему отношению элементов столбца свободных членов к соответствующим положительным элементам разрешающего столбца
I:
S: Последняя симплексная таблица решения ЗЛП на максимум имеет вид
 i
i
| Базис |

|

|

|

| -1

|

| -1

|

| -1 | |||||||

| -3 | |||||||

| -1 | |||||||
  
| 
|
Как видно из таблицы, задача:
-: не имеет оптимального плана
-: имеет оптимальный план 
+: имеет оптимальный план 
-: имеет оптимальный план 
I:
S: Задача ЛП имеет бесконечное множество оптимальных решений, если в индексной строке последней симплексной таблицы, содержащей оптимальный план:
-: имеется хотя бы одна положительная оценка
-: все оценки свободных переменных положительны
+: имеется хотя бы одна нулевая оценка, соответствующая свободной переменной
-: имеются нулевые оценки
I:
S: Последняя симплексная таблица решения ЗЛП на минимум имеет вид
 I
I
| Базис |

|

|

|

| -4

|

|

|

| 5/2 | 1/4 | ||||||

| -4 | -1/2 | 1/4 | 1/2 | ||||
  
| 
| -12 | -1 | -2 |
Как видно из таблицы, задача имеет:
+: единственный оптимальный план
-: альтернативный оптимум
-: не имеет решения
I:
S: ЗЛП на максимум имеет единственный оптимальный план, если в индексной строке симплексной таблицы, содержащей оптимальный план:
-: все оценки неотрицательны
-: все оценки свободных переменных неотрицательны
+: все оценки свободных переменных положительны
-: имеются нулевые оценки
I:
S: Целевая функция ЗЛП на максимум на множестве допустимых планов не ограничена сверху, если в индексной строке симплексной таблицы содержится:
-: нулевая оценка свободной переменной
+: отрицательная оценка ∆jо, а в соответствующем столбце хjо нет ни одного положительного элемента
-: положительная оценка ∆jо, а в соответствующем столбце хjо нет ни одного отрицательного элемента
-: отрицательная оценка ∆jо, а в соответствующем столбце хjо нет ни одного нулевого элемента
I:
S: Если в индексной строке симплексной таблицы ЗЛП на минимум содержится положительная оценка ∆jо > 0, а в столбце переменной хjо нет ни одного положительного элемента, то:
-: найден оптимальный план
+: целевая функция не ограничена снизу
-: целевая функция ограничена снизу
-: целевая функция не ограничена сверху
I:
S: Базисный план ЗЛП, записанной в предпочтительном виде, вырожден, если среди
-: коэффициентов целевой функции нет отрицательных
-: свободных членов уравнений нет отрицательных
+: свободных членов уравнений имеются нули
-: коэффициентов целевой функции имеются нули
I:
S: Конечность симплексного метода следует из:
-: универсальности метода в классе ЗЛП
+: конечности числа опорных планов
-: существования допустимых планов
-: линейности целевой функции
I:
S: Последняя симплексная таблица решения ЗЛП на максимум имеет вид
 I
I
| Базис |

|

|

|

|

|

|

|

| -1 | |||||||

| -1 | |||||||

| -3 | |||||||
  
| 
|
Как видно из таблицы, задача имеет:
+: единственный оптимальный план
-: альтернативный оптимум
-: не имеет решения
I:
S: Пусть ЗЛП симплексным методом решается на максимум. Тогда для значений целевой функции на двух последовательных итерациях F1 и F2 справедливо соотношение:
-: F1 = F2
-: F1 > F2
+: F1 ≤ F2
-: F1 = -F2
I:
S: Для значений целевой функции F1 и F2 ЗЛП на минимум, полученных на двух последовательных итерациях, имеет место:
-: F1 = -F2
+: F1 ≥ F2
-: F1 ≤ F2
-: F1 = F2
I:
S: Симплексная таблица очередного шага решения ЗЛП на максимум имеет вид
 I
I
| Б |

|

|

| -6

|

|

|

|

|

| -5/3 | 5/3 | -1/3 | ||||||

| -1/3 | -2/3 | 1/3 | ||||||

| -1 | -9 | |||||||

| -11/3 | 8/3 | 5/3 |
Как видно из таблицы, задача:
+: не имеет оптимального плана
-: имеет оптимальный план и он находится в таблице
-: не имеет опорных планов.
I:
S: Если все искусственные переменные выведены из базиса (метод искусственного базиса) и план не является оптимальным, то для ЗЛП на min разрешающий столбец выбирается
-: по наибольшему положительному числу в (m+2) – й строке
-: по наименьшему отрицательному числу в (m+1) – ой строке
-: по наибольшему отрицательному числу в (m+1) – ой строке
+: по наибольшему положительному числу в (m+1) – ой строке
I:

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!