-: минимизировать количество потребляемых продуктов
-: максимизировать количество питательных веществ в продуктах питания
-: максимизировать прибыль
+: минимизировать издержки на рацион питания
I:
S: При преобразовании задачи линейного программирования к каноническому виду, дополнительные переменные вводятся в целевую функцию с коэффициентами,
+: равными нулю
-: равными очень большим положительным числам
-: равными правым частям соответствующих ограничений
-: равными единице
I:
S: Задача линейного программирования
max Z = С ∙ X
А1х1 + … + Аn ∙ хn = А0, X 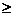 0
0
задана
-: в общей форме
-: в скалярной форме
+: в векторной форме
-: в стандартной форме
I:
S: Для задачи о наилучшем использовании ресурсов дополнительные переменные показывают:
+: величину неиспользованного ресурса
-: величину ресурса, использованного в оптимальном плане
-: дополнительную прибыль от сэкономленного ресурса
-: стоимость соответствующего потребляемого ресурса
I:
S: Для задачи о смесях дополнительная переменная показывает:
-: потребление соответствующего питательного вещества в пределах нормы
+: потребление соответствующего питательного вещества в оптимальном плане сверх нормы
-: стоимость соответствующего потребляемого вещества
-: величину ресурса, использованного в оптимальном плане
I:
S: В задаче о рационе требуется:
+: минимизация общей стоимости всех кормов
-: максимизация содержания питательных веществ в кормах
-: минимизация количества кормов
-: минимизация стоимости всех питательных веществ
I:
S: Если какая-то переменная хк задачи ЛП не подчинена условию не отрицательности, то ее следует:
-: исключить из числа переменных
+: заменить двумя неотрицательными переменными, приняв хк = uk – vk
-: увеличить в два раза
-: обнулить
I:
S: Пусть х* - оптимальный план задачи ЛП на max с целевой функцией F. Тогда для любого допустимого плана х выполняется соотношение:
-: F (x) = F (x*)
-: F (x) > F (x*)
+: F (x) ≤ F (x*)
-: F (x) = - F (x*)
I:
S: Если х* - оптимальный план задачи ЛП на min, F – целевая функция, а x - любой допустимый план задачи, то справедливо следующее соотношение:
+: F (x) ≥ F (x *)
-: F (x *) + F (x) = 0
-: F (x *) ∙ F (x) = 1
-: F (x) = F (x*)
I:
S: Линейное программирование это
-: один из приемов разработки программного обеспечения ЭВМ
+: математический метод оптимизации
-: определение последовательности действий при проведении общественных мероприятий
-: составление программ линейной структуры
I:
S: В линейном программировании используются функции, уравнения и неравенства
-: преимущественно линейные
+: только линейные
-: любые
-: в зависимости от решаемой задачи
I:
S: Методы линейного программирования позволяют определить оптимальное экономическое решение
-: всегда
+: да, если оно существует
-: линейное программирование предназначено для других целей
I:
S: Конкретный план в линейном программировании представляется
-: датами
+: числовыми значениями
-: интегральной кривой возможных потерь
-: кривыми спроса
I:
S: Оптимальный план задачи ЛП это
-: любой план
-: любой допустимый план
+: допустимый план, которому соответствует максимум выручки
-: любой опорный план
I:
S: Система ограничений задачи ЛП это система
-: нестрогих неравенств
-: только строгих неравенств
-: только равенств
+: равенств и неравенств
I:
S: Допустимыми являются планы
-: любые
-: любые с положительными значениями
+: удовлетворяющие системе ограничений
-: любые с ненулевыми значениями
I:
S: Целевая функция задачи линейного программирования должна быть
-: нелинейной
+: линейной
-: любой
-:выпуклой
I
S: Математическая модель задачи линейного программирования это
-: целевая функция
+: целевая функция и набор ограничений
-: набор ограничений
I:
S: Методом линейного программирования решаются задачи поиска экстремума
-: нелинейной функции при линейных ограничениях
-: линейной функции при нелинейных ограничениях;
+: линейной функции при линейных ограничениях.
I:
S: Допустимым планом задачи является
-: любой план
+: любой план, обеспечивающий выполнение ограничений
-: это зависит от конкретного содержания задачи
-: любой план с ненулевыми значениями
S: Оптимальным планом задачи является план
-: любой, обеспечивающий выполнение ограничений
-: доставляющий экстремум целевой функции
+: доставляющий экстремум целевой функции при выполнении ограничений
-: любой с ненулевыми значениями
I:
S: В задаче линейного программирования допустимо количество ограничений
+: не более числа переменных
-: равное числу переменных
-: любое
-: не более 1000
I:
S: Максимальное значение функции  при ограничениях
при ограничениях

равно
-: 8
-: 5
+: 6
-: 1
I:
S: Максимальное значение функции  при ограничениях
при ограничениях

равно
-: 0
-: -1
-: -2
+: -3
I:
S: Максимальное значение функции  при ограничениях
при ограничениях

равно
-: 12
-: 14
+: 16
-: 18
I:
S: Максимальное значение функции  при ограничениях
при ограничениях

равно
-: 23
-: 6
+: 22
-: 14
I:
S: Максимальное значение функции  при ограничениях
при ограничениях

равно
-: 14
-: 16
-: 22
+: 30
I:
S: Для изготовления изделий  и
и 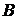 склад может отпустить металла не более 80 кг, причем на одно изделие
склад может отпустить металла не более 80 кг, причем на одно изделие  расходуется 2 кг, а на изделие
расходуется 2 кг, а на изделие 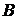 - 1кг металла. Укажите план производства, при котором обеспечен наибольший доход, если изделий
- 1кг металла. Укажите план производства, при котором обеспечен наибольший доход, если изделий  требуется изготовить не более 30 шт., а изделий
требуется изготовить не более 30 шт., а изделий 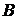 - не более40 шт., причем одно изделие
- не более40 шт., причем одно изделие  стоит 5 ден.ед., а одно изделие
стоит 5 ден.ед., а одно изделие 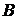 -3 ден.ед.
-3 ден.ед.
+: 
-: 
-: 
-: 
-: 
I:
S: Если вся выпускаемая продукция или ее часть реализуется комплектами, то в модели задачи необходимо изменить
-: целевую функцию и систему ограничений
-: только целевую функцию
+: только систему ограничений
I:
S: Если предприятие может пополнять объемы ресурсов, неся связанные с этим затраты, но и расширяя свои производственные возможности, то в модели задачи необходимо изменить
-: только целевую функцию
+: целевую функцию и систему ограничений
-: только систему ограничений



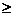 0
0 при ограничениях
при ограничениях

 при ограничениях
при ограничениях
 при ограничениях
при ограничениях
 при ограничениях
при ограничениях
 и
и 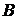 склад может отпустить металла не более 80 кг, причем на одно изделие
склад может отпустить металла не более 80 кг, причем на одно изделие 







