Дифференциальным уравнением первого порядка называется уравнение вида:  или
или 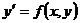 . Его общее решение содержит одну произвольную постоянную С:
. Его общее решение содержит одну произвольную постоянную С: 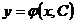 .
.
Дифференциальные уравнения первого порядка иногда удобно записывать и в виде:
 .
.
Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения.
Если функции 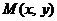 и
и  разлагаются на множители:
разлагаются на множители: 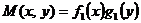 , а
, а  , тогда уравнение вида:
, тогда уравнение вида:

называется уравнением с разделяющимися переменными.
Предположив, что  , и разделив обе части первого уравнения на
, и разделив обе части первого уравнения на  , получим уравнение с разделенными переменными:
, получим уравнение с разделенными переменными:
 ,
,
которое интегрируется:
 .
.
Вычисление полученных интегралов и дает общее решение уравнения с разделяющимися переменными.
Функция  называется однородной функцией измерения
называется однородной функцией измерения  (
( ) относительно аргументов х и у, если равенство
) относительно аргументов х и у, если равенство  справедливо для любого
справедливо для любого  , при котором функция
, при котором функция  определена.
определена.
Если 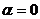 , то функция будет однородной нулевого измерения
, то функция будет однородной нулевого измерения  .
.
Дифференциальное уравнение первого порядка  называется однородным, если
называется однородным, если 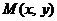 и
и  - однородные функцииот х и у одинакового измерения, т.е.
- однородные функцииот х и у одинакового измерения, т.е.  Действительно, переписав его в виде:
Действительно, переписав его в виде: 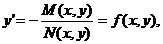 легко заключаем, что
легко заключаем, что  - однородная функция нулевого измерения, поскольку:
- однородная функция нулевого измерения, поскольку:

Так как однородное дифференциальное уравнение первого порядка всегда можно записать в виде  то, положив
то, положив  , получим:
, получим:

Данное уравнение решается с помощью замены  и сводится к уравнению с разделяющимися переменными относительно х и новой функции
и сводится к уравнению с разделяющимися переменными относительно х и новой функции  :
:
 . Отсюда следует:
. Отсюда следует: 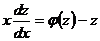 . Разделив переменные и выполнив почленное интегрирование, находят общее решение однородного дифференциального уравнения первого порядка.
. Разделив переменные и выполнив почленное интегрирование, находят общее решение однородного дифференциального уравнения первого порядка.
Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли.
Дифференциальное уравнение первого порядка:

называется линейным, если оно линейно относительно неизвестной функции у и ее производной  , где
, где  и
и  - непрерывные функции от х.
- непрерывные функции от х.
Линейное дифференциальное уравнение первого порядка называется однородным, если  , в противном случае оно неоднородное.
, в противном случае оно неоднородное.
Линейное дифференциальное уравнение можно проинтегрировать методом Бернулли, суть которого заключается в следующем. Представим искомую функцию  в виде произведения двух неизвестных функций
в виде произведения двух неизвестных функций  и
и  по формуле
по формуле 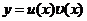 (подстановка Бернулли).Тогда
(подстановка Бернулли).Тогда 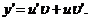 Подставив выражения для у и у’ в линейное дифференциальное уравнение, получим:
Подставив выражения для у и у’ в линейное дифференциальное уравнение, получим:
 ,
,
которое преобразуем к виду:
 .
.
Так как  , то интегрирование данного вида уравнения сводится к интегрированию двух уравнений с разделяющимися переменными:
, то интегрирование данного вида уравнения сводится к интегрированию двух уравнений с разделяющимися переменными:
 и
и 
Найдя общее решение  изпервого уравнения, а затем и
изпервого уравнения, а затем и  из второго уравнения, придем к общему решению линейного уравнения:
из второго уравнения, придем к общему решению линейного уравнения: 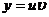 .
.
Дифференциальное уравнение
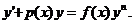
где 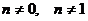 , называется уравнением Бернулли.
, называется уравнением Бернулли.
Путем введения новой функции  по формуле
по формуле  , откуда
, откуда 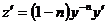 , уравнение Бернулли сводится к линейному уравнению относительно этой функции:
, уравнение Бернулли сводится к линейному уравнению относительно этой функции:

Уравнение Бернулли, как и линейное уравнение можно решить с помощью подстановки Бернулли 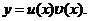
Линейные дифференциальные уравнения второго порядка. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами .
Уравнение вида:
 ,
,
где  - заданные непрерывные функции от х, называется линейным неоднородным дифференциальным уравнением второго порядка, а соответствующее ему уравнение:
- заданные непрерывные функции от х, называется линейным неоднородным дифференциальным уравнением второго порядка, а соответствующее ему уравнение:

- линейным однородным.
Если 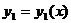 и
и  - какие-нибудь два линейно независимых частных решения однородного дифференциального уравнения второго порядка, то его общим решением служит функция:
- какие-нибудь два линейно независимых частных решения однородного дифференциального уравнения второго порядка, то его общим решением служит функция:
 .
.
Функции  и
и 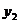 называются линейно независимыми, если при постоянных
называются линейно независимыми, если при постоянных  и
и  тождество
тождество  выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда  Если же хотя бы одна из них отлична от нуля, а тождество
Если же хотя бы одна из них отлична от нуля, а тождество  возможно, то эти решения
возможно, то эти решения  и
и 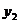 называются линейно зависимыми.
называются линейно зависимыми.
Общее решение линейного неоднородного дифференциального уравнения второго порядка есть сумма его частного решения и общего решения соответствующего ему линейного однородного дифференциального уравнения:
 ,
,
где 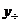 - частное решение неоднородного, а
- частное решение неоднородного, а  - общее решение однородного уравнения.
- общее решение однородного уравнения.
Пусть требуется решить линейное однородное дифференциальное уравнение второго порядка:
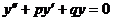 ,
,
в котором  и
и  - постоянные величины.
- постоянные величины.
Найдём частные решения дифференциального уравнения в виде 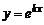 . Тогда
. Тогда  ,
,  . Подставив выражения
. Подставив выражения  ,
,  и
и  в исходное уравнение, получим:
в исходное уравнение, получим:
 .
.
Так как  , то получим уравнение
, то получим уравнение
 ,
,
которое называется характеристическим уравнением линейного однородного дифференциального уравнения второго порядка.
Таким образом, 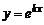 является частным решением линейного однородного дифференциального уравнения второго порядка, если
является частным решением линейного однородного дифференциального уравнения второго порядка, если  - корень характеристического уравнения.
- корень характеристического уравнения.
В зависимости от дискриминанта корни характеристического уравнения могут быть:
1) действительными и различными  , тогда частные решения
, тогда частные решения 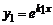 и
и  , а общее решение:
, а общее решение:
 ,
,
2) действительными и равными  , тогда частные решения
, тогда частные решения  и
и  , а общее решение:
, а общее решение:
 ,
,
3) комплексными  ,
,  , тогда частные решения
, тогда частные решения  и
и  , а общее решение:
, а общее решение:
 .
.
Общее решение линейного неоднородного дифференциального уравнения второго порядка:
 ,
,
в котором  и
и  - постоянные величины, находится как:
- постоянные величины, находится как:
 ,
,
где 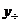 - частное решение неоднородного, а
- частное решение неоднородного, а  - общее решение однородного уравнения.
- общее решение однородного уравнения.
 ,
,
Общее решение однородного уравнения, как известно, находится с помощью характеристического уравнения, а частное решение неоднородного уравнения находится в зависимости от вида функции  .
.
1) если 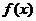 есть многочлен
есть многочлен  -ой степени:
-ой степени:
 ,
,
в частности, многочлен второй степени  (
( ), то частное решение неоднородного уравнения ищется в виде:
), то частное решение неоднородного уравнения ищется в виде:
а)  при
при  и
и  ;
;
б)  при
при  и
и  ;
;
в) при  и
и  неоднородное дифференциальное уравнение принимает вид:
неоднородное дифференциальное уравнение принимает вид:  , решение которого находится непосредственным двукратным интегрированием, т.е.
, решение которого находится непосредственным двукратным интегрированием, т.е.  , затем,
, затем, 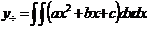 .
.
2) Если 
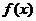 - показательная функция, т.е.
- показательная функция, т.е.  (
( ), то частное решение неоднородного уравнения ищется в виде:
), то частное решение неоднородного уравнения ищется в виде:
а)  , если коэффициент
, если коэффициент  не является корнем характеристического уравнения, т.е.
не является корнем характеристического уравнения, т.е. 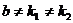 ;
;
б)  , если коэффициент
, если коэффициент  является однократным корнем характеристического уравнения, т.е.
является однократным корнем характеристического уравнения, т.е.  ;
;
в)  , если коэффициент
, если коэффициент  является двукратным корнем характеристического уравнения, т.е.
является двукратным корнем характеристического уравнения, т.е.  .
.
3) Если 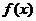 - тригонометрическая функция, т.е.
- тригонометрическая функция, т.е. 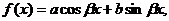
 , то частное решение неоднородного уравнения ищется в виде:
, то частное решение неоднородного уравнения ищется в виде:
а)  , если
, если  ;
;
б)  если
если  , а
, а  .
.
Числовые ряды.
Пусть дана числовая последовательность  .
.
Выражение вида  называется числовым рядом или просто рядом.
называется числовым рядом или просто рядом.
При этом числа  называются членами ряда, а член
называются членами ряда, а член  с произвольным номером — общим членом ряда.
с произвольным номером — общим членом ряда.
Суммы конечного числа членов ряда:
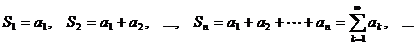
называются частичными суммами ряда. Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм  .
.
Если все члены ряда положительны, то ряд называется знакоположительным.
Ряд называется сходящимся, если предел  -частичной суммы существует и конечен, т.е.
-частичной суммы существует и конечен, т.е.  , в противном случае говорят, что ряд расходится. При этом
, в противном случае говорят, что ряд расходится. При этом 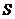 называется суммой ряда.
называется суммой ряда.
Ряд: 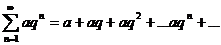 ,
,
где  - знаменатель геометрической прогрессии, называется рядом геометрической прогрессии.
- знаменатель геометрической прогрессии, называется рядом геометрической прогрессии.
 -частичная сумма ряда геометрической прогрессии равна:
-частичная сумма ряда геометрической прогрессии равна:
 =
= 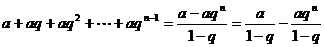 .
.
Ряд геометрической прогрессии является сходящимся при  (его сумма
(его сумма  ) ирасходящимся при
) ирасходящимся при  .
.
Свойства сходящихся рядов:
4. Если сходится ряд:

то сходится и ряд 
и обратно, если сходится второй ряд, то сходится и первый.
Другими словами, на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.
2) Если ряд 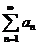 сходится и его сумма равна
сходится и его сумма равна 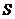 , то и ряд
, то и ряд  , где с — некоторое число, также сходится, и его сумма равна
, где с — некоторое число, также сходится, и его сумма равна  .
.
5. Если ряды 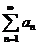 и
и  сходятся и их суммы соответственно равны
сходятся и их суммы соответственно равны 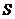 и
и 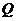 , то и ряд
, то и ряд  cходится и его сумма равна
cходится и его сумма равна  .
.
Таким образом, установлено, что сходящиеся ряды можно умножать на число, почленно складывать и вычитать так же, как и конечные суммы.





 или
или 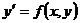 . Его общее решение содержит одну произвольную постоянную С:
. Его общее решение содержит одну произвольную постоянную С: 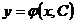 .
. .
.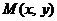 и
и  разлагаются на множители:
разлагаются на множители: 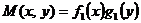 , а
, а  , тогда уравнение вида:
, тогда уравнение вида:
 , и разделив обе части первого уравнения на
, и разделив обе части первого уравнения на  , получим уравнение с разделенными переменными:
, получим уравнение с разделенными переменными: ,
,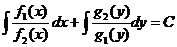 .
. называется однородной функцией измерения
называется однородной функцией измерения  (
( ) относительно аргументов х и у, если равенство
) относительно аргументов х и у, если равенство  справедливо для любого
справедливо для любого  , при котором функция
, при котором функция  определена.
определена.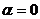 , то функция будет однородной нулевого измерения
, то функция будет однородной нулевого измерения 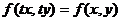 .
. Действительно, переписав его в виде:
Действительно, переписав его в виде: 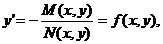 легко заключаем, что
легко заключаем, что 
 то, положив
то, положив  , получим:
, получим:
 и сводится к уравнению с разделяющимися переменными относительно х и новой функции
и сводится к уравнению с разделяющимися переменными относительно х и новой функции  :
: . Отсюда следует:
. Отсюда следует: 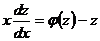 . Разделив переменные и выполнив почленное интегрирование, находят общее решение однородного дифференциального уравнения первого порядка.
. Разделив переменные и выполнив почленное интегрирование, находят общее решение однородного дифференциального уравнения первого порядка.
 , где
, где  и
и  - непрерывные функции от х.
- непрерывные функции от х. , в противном случае оно неоднородное.
, в противном случае оно неоднородное. в виде произведения двух неизвестных функций
в виде произведения двух неизвестных функций  и
и  по формуле
по формуле 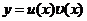 (подстановка Бернулли).Тогда
(подстановка Бернулли).Тогда 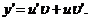 Подставив выражения для у и у’ в линейное дифференциальное уравнение, получим:
Подставив выражения для у и у’ в линейное дифференциальное уравнение, получим: ,
, .
. , то интегрирование данного вида уравнения сводится к интегрированию двух уравнений с разделяющимися переменными:
, то интегрирование данного вида уравнения сводится к интегрированию двух уравнений с разделяющимися переменными: и
и 
 изпервого уравнения, а затем и
изпервого уравнения, а затем и  из второго уравнения, придем к общему решению линейного уравнения:
из второго уравнения, придем к общему решению линейного уравнения: 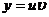 .
.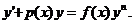
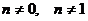 , называется уравнением Бернулли.
, называется уравнением Бернулли. по формуле
по формуле  , откуда
, откуда 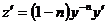 , уравнение Бернулли сводится к линейному уравнению относительно этой функции:
, уравнение Бернулли сводится к линейному уравнению относительно этой функции:
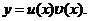
 ,
, - заданные непрерывные функции от х, называется линейным неоднородным дифференциальным уравнением второго порядка, а соответствующее ему уравнение:
- заданные непрерывные функции от х, называется линейным неоднородным дифференциальным уравнением второго порядка, а соответствующее ему уравнение:
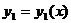 и
и  - какие-нибудь два линейно независимых частных решения однородного дифференциального уравнения второго порядка, то его общим решением служит функция:
- какие-нибудь два линейно независимых частных решения однородного дифференциального уравнения второго порядка, то его общим решением служит функция: .
. и
и 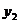 называются линейно независимыми, если при постоянных
называются линейно независимыми, если при постоянных  и
и  тождество
тождество  выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда  Если же хотя бы одна из них отлична от нуля, а тождество
Если же хотя бы одна из них отлична от нуля, а тождество  ,
,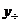 - частное решение неоднородного, а
- частное решение неоднородного, а  - общее решение однородного уравнения.
- общее решение однородного уравнения.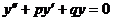 ,
, и
и  - постоянные величины.
- постоянные величины.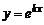 . Тогда
. Тогда  ,
,  . Подставив выражения
. Подставив выражения  и
и  в исходное уравнение, получим:
в исходное уравнение, получим: .
. , то получим уравнение
, то получим уравнение ,
, - корень характеристического уравнения.
- корень характеристического уравнения. , тогда частные решения
, тогда частные решения 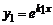 и
и  , а общее решение:
, а общее решение: ,
, , тогда частные решения
, тогда частные решения  и
и  , а общее решение:
, а общее решение: ,
, ,
,  , тогда частные решения
, тогда частные решения  и
и  , а общее решение:
, а общее решение: .
. ,
, .
.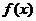 есть многочлен
есть многочлен  -ой степени:
-ой степени: ,
, (
( ), то частное решение неоднородного уравнения ищется в виде:
), то частное решение неоднородного уравнения ищется в виде: при
при  и
и  ;
; при
при  ;
; и
и  , решение которого находится непосредственным двукратным интегрированием, т.е.
, решение которого находится непосредственным двукратным интегрированием, т.е.  , затем,
, затем, 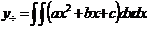 .
.
 (
( , если коэффициент
, если коэффициент  не является корнем характеристического уравнения, т.е.
не является корнем характеристического уравнения, т.е. 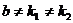 ;
; , если коэффициент
, если коэффициент  ;
; , если коэффициент
, если коэффициент  .
.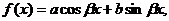
 , то частное решение неоднородного уравнения ищется в виде:
, то частное решение неоднородного уравнения ищется в виде: , если
, если  если
если  .
. .
. называется числовым рядом или просто рядом.
называется числовым рядом или просто рядом. с произвольным номером — общим членом ряда.
с произвольным номером — общим членом ряда.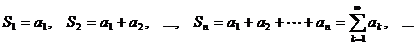
 .
. , в противном случае говорят, что ряд расходится. При этом
, в противном случае говорят, что ряд расходится. При этом 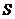 называется суммой ряда.
называется суммой ряда.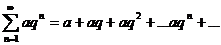 ,
, =
= 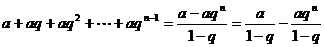 .
. (его сумма
(его сумма  ) ирасходящимся при
) ирасходящимся при  .
.

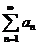 сходится и его сумма равна
сходится и его сумма равна  , где с — некоторое число, также сходится, и его сумма равна
, где с — некоторое число, также сходится, и его сумма равна  .
. сходятся и их суммы соответственно равны
сходятся и их суммы соответственно равны  , то и ряд
, то и ряд  cходится и его сумма равна
cходится и его сумма равна  .
.


