

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
Топ:
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Число А называется пределом числовой последовательности { хn }, если для любого  >0 существует номер N=N(
>0 существует номер N=N(  )>0, такой, что для всех п>N выполняется неравенство | хп—A |<
)>0, такой, что для всех п>N выполняется неравенство | хп—A |<  . Если А –предел последовательности { хn }, то это записывается следующим образом
. Если А –предел последовательности { хn }, то это записывается следующим образом

Последовательность, имеющая предел, называется сходящейся,в противном случае – расходящейся.
Пусть функция у=f(х) определена в некоторой окрестности точки х 0. Тогда число А называется пределомфункции у = f (х) при х  х 0 (в точке х = х 0), если для любого
х 0 (в точке х = х 0), если для любого  >0 существует
>0 существует 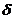 =
= 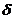 (
( )>0, такое, что при 0 <| х—х 0|<
)>0, такое, что при 0 <| х—х 0|< 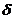 справедливо неравенство | f (х)- А |<
справедливо неравенство | f (х)- А |<  .
.
Если А – предел функции f (х) при х  х 0, то записывают это так
х 0, то записывают это так

В самой точке х 0функция f (х)может и не существовать (f (х 0) не определено). Аналогично запись  обозначает, что для любого
обозначает, что для любого  >0 существует N = N (
>0 существует N = N ( )>0, такое, что при | х|>N выполняется неравенство | f (х) -А| <
)>0, такое, что при | х|>N выполняется неравенство | f (х) -А| <  .
.
Если существует предел вида  , который обозначают также
, который обозначают также  или f (х 0 - 0), то он называется пределом слева функции f (х)в точке x 0. Аналогично если существует предел вида
или f (х 0 - 0), то он называется пределом слева функции f (х)в точке x 0. Аналогично если существует предел вида  (в другой записи
(в другой записи  или f (x 0+0)), то он называется пределом справафункции f (х)в точке x 0. Пределы слева и справа называются односторонними. Для существования предела функции f(х)в точке x 0необходимо и достаточно, чтобы оба односторонних предела в точке x 0существовали и были равны, то есть f (x 0-0)=f(x 0+0).
или f (x 0+0)), то он называется пределом справафункции f (х)в точке x 0. Пределы слева и справа называются односторонними. Для существования предела функции f(х)в точке x 0необходимо и достаточно, чтобы оба односторонних предела в точке x 0существовали и были равны, то есть f (x 0-0)=f(x 0+0).
Справедливы следующие основные теоремы о пределах.
Теорема 1. Пусть существуют  (i =1,…, п). Тогда
(i =1,…, п). Тогда

Теорема 2. Пусть существуют  и
и  Тогда
Тогда
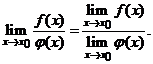
Эти утверждения сохраняются и при х 0 =  .
.
Если условия этих теорем не выполняются, то могут возникнуть неопределенности вида 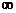 -
- 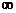 ,
,  ,
,  и др., которые в простейших случаях раскрываются с помощью алгебраических преобразований.
и др., которые в простейших случаях раскрываются с помощью алгебраических преобразований.
Замечательные пределы. Сравнение бесконечно малых функций.
Широко используются следующие два предела
1) 
2)  ,
,
которые называются соответственно первым и вторым замечательными пределами.
Если  (т. Е. для любого
(т. Е. для любого  > 0 существует число
> 0 существует число 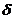 >0, такое что при 0<
>0, такое что при 0<  <
< 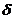 справедливо неравенство
справедливо неравенство  <
<  ), то
), то  называется бесконечно малойфункцией или величиной при х
называется бесконечно малойфункцией или величиной при х  .
.
Для сравнения двух бесконечно малых функций  и
и  при х
при х  находят предел их отношения
находят предел их отношения
 (1)
(1)
Если С  0, то
0, то  и
и  называются бесконечно малыми величинами одного и того же порядка;если С =0, то
называются бесконечно малыми величинами одного и того же порядка;если С =0, то  называется бесконечно малой более высокого порядка по сравнению с
называется бесконечно малой более высокого порядка по сравнению с  , а
, а  - бесконечно малой более низкого порядка по сравнению с
- бесконечно малой более низкого порядка по сравнению с  .
.
Если  (0<
(0<  <
< 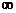 ),
),  то
то  называется бесконечно малойпорядка k, по сравнению с
называется бесконечно малойпорядка k, по сравнению с  при х
при х  .
.
Если 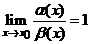 , то бесконечно малые
, то бесконечно малые  и
и  при х
при х  называются эквивалентными(равносильными) величинами и обозначают
называются эквивалентными(равносильными) величинами и обозначают  ~
~  .
.
Например, при х 
 ~
~  ,
, 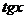 ~ х,
~ х,  ~ х,
~ х,  — 1~
— 1~  ..
..
Легко доказать, что предел отношения бесконечно малых функций  и
и  при х
при х  равен пределу отношения эквивалентных им бесконечно малых функций
равен пределу отношения эквивалентных им бесконечно малых функций  и
и  при х
при х  , т.е. верны предельные равенства
, т.е. верны предельные равенства

Непрерывность функции. Классификация
Точек разрыва функции.
Функция у = f (х)называется непрерывной при х = x 0 (в точке x 0), если:
1) функция f (х) определена в точке x 0и ее окрестности;
2) существует конечный предел функции f (х)в точке x 0;
3) этот предел равен значению функции в точке x 0, то есть
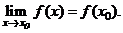 (2)
(2)
Если положить х=x0 + 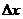 , то условие непрерывности (2) будет равносильно условию
, то условие непрерывности (2) будет равносильно условию

т. Е. функция у = f (х)непрерывна в точке x 0тогда и только тогда, когда бесконечно малому приращению аргумента 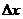 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции  .
.
Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.
Точка x 0, в которой нарушено хотя бы одно из трех условий непрерывности функции, называется точкой разрывафункции. Если в точке x 0существуют конечные пределы f (x 0 - 0) и f (x 0 +0), такие, что f (x 0 - 0)  f (x 0+0), то x 0называется точкой разрыва первого рода. Если хотя бы один из пределов f (x 0 - 0) и f (x 0+0) не существует или равен бесконечности, то точку x 0называют точкой разрыва второго рода. Если f (x 0 - 0) =f (x 0 +0) и функция f (х)не определена в точке x 0, то точку x 0называют устранимой точкой разрыва функции.
f (x 0+0), то x 0называется точкой разрыва первого рода. Если хотя бы один из пределов f (x 0 - 0) и f (x 0+0) не существует или равен бесконечности, то точку x 0называют точкой разрыва второго рода. Если f (x 0 - 0) =f (x 0 +0) и функция f (х)не определена в точке x 0, то точку x 0называют устранимой точкой разрыва функции.
|
|
|

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2026 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!