Взаимно перпендикулярных колебаний

 

Цель работы: изучение закона сложения гармонических взаимно перпендикулярных колебаний на «песочном маятнике»; получение траектории сложного движения.

Приборы и принадлежности: «песочный маятник», воронка, песок, секундомер, мас­штабная линейка.

Простейшим видом колебательных движений является гармоническое колебание.

Оно возникает в том случае, если на тело, выведенное из положения равновесия, дейст­вует сила, направленная всегда к положению равновесия, а по величине пропорцио­нальная смещению тела от положения равновесия. Таким образом, можно написать

F = – ks,

где F – сила, под действием которой тело совершает гармоническое колебание, s – сме­щение тела от положения равновесия, k – некоторый постоянный коэффициент.

Это выражение можно написать и в таком виде

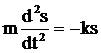, (1)

где m – масса колеблющегося тела и 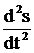– его ускорение, которое выражено в дифференциальной форме, так как в колебательном движении оно является величиной пере­менной. Решением уравнения (1) есть функция синуса (или косинуса)

s = a sin (wt + j), (2)

которое описывает гармоническое колебание величины s, где а – амплитуда колебания, w круговая (циклическая) частота, j – начальная фаза колебания в момент вре­мени t = 0, (wt + j) – фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как синус изменяется в пределах от +1 до –1, то s может принимать значения от + а до – а. Циклическая часто­та связана с периодом колебаний соотношением 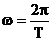, где Т – период колебаний, т.е. период времени, за который фаза колебаний получает приращение 2p.

При изучении колебательных движений большой интерес представляют вопросы, связанные со сложением колебаний. Ограничимся анализом сложения взаимно перпен­дикулярных гармонических колебаний. Если материальная точка участвует одновре­менно в двух взаимно перпендикулярных гармонических колебаниях одинаковой часто­ты в направлении осей х и у, то ее смещение по этим направлениям в любой момент времени равно

х = а cos wt (3)

у = b cos (wt + j),

где a, b – амплитуды колебаний, w – одинаковая для обоих колебаний циклическая частота, j – начальная разность фаз. Выражение (3) представляет собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Для получения уравнения траектории в обычном виде в координатной форме исключим из уравнения (3) параметр t.

Записывая складываемые колебания в виде

;

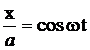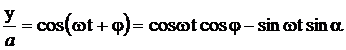
и заменяя во втором уравнении cos wt на 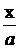и sin wt на 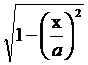, получим после несложных преобразований уравнение эллипса, оси которого ориентированы относитель­но координатных осей произвольно (рис.1б):

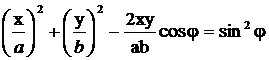. (4)

Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз j. Рассмотрим некоторые частные случаи, представляющие физический интерес:

а) если разность фаз колебаний равна нулю или четному числу p, т.е. 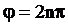, то из уравнения (4) находим

,

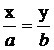т.е. уравнение прямой, которая геометрически изображается диагональю АС прямо­угольника ABCD (рис.2а), построенного на складываемых колебаниях. Диагональ АС следует рассматривать как эллипс предельного вида, вытянутый в отрезок прямой ли­нии, т.е. с малой осью, равной нулю.

 

б) Если разность фаз колебаний равна нечетному числу p, т.е. 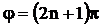, то из этого же уравнения находим:

,

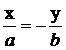т.е. уравнение прямой, второй диагонали BD, того же прямоугольника (рис.2б), которая также является предельным случаем эллипса.

в) Если разность начальных фаз складываемых колебаний равна 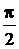, то получаем:

,

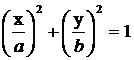т.е. уравнение эллипса, отнесенное к осям х, у (рис.2в).

г) Если, кроме того, в последнем случае амплитуды обоих колебаний равны, то получа­ем: х² +у² = а ², т.е. уравнение окружности (рис.2г) радиуса а.

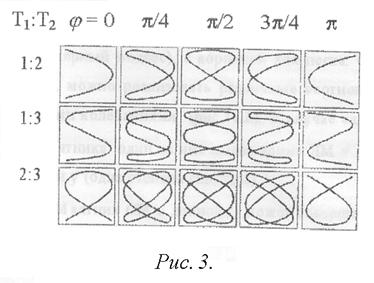
При сложении двух гармони­ческих колебаний с разными перио­дами колебаний траектория суммар­ного колебания оказывается значи­тельно сложней: она определяется относительной величиной амплитуд обоих колебаний, отношением их периодов (частот) и разностью на­чальных фаз. При сложении взаимно перпендикулярных колебаний получаются периодические (замкнутые) кривые различного вида, называемые фигурами Лиссажу. Некоторые из них даны на рис.3. Отношение периодов указано на рисунке.

 

Описание прибора

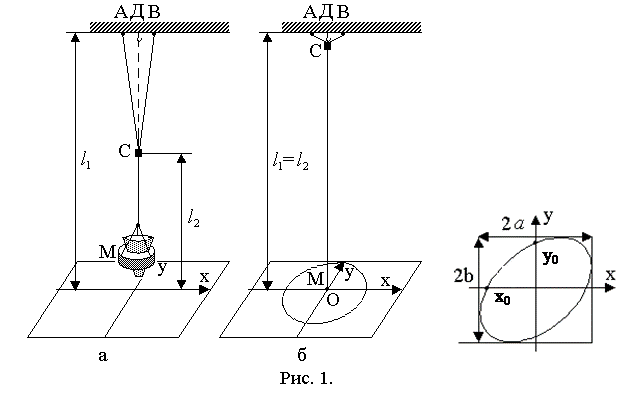
Для наблюдения траектории результирующего движения, получающегося при сложении двух взаимно перпендикулярных, колебаний используется «песочный» маят­ник (рис.1).

«Песочный» маятник, используемый в лабораторной работе, представляет мате­матический маятник (простейший маятник).

Математическим маятником называется массивное тело, подвешенное на нити, масса которой пренебрежимо мала по сравнению с массой тела, и длина нити велика по сравнению с размерами тела. Таким образом, с достаточной точностью выполняется формула

,

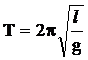где Т – период колебаний математического маятника, l – его длина, g – ускорение силы тяжести.

Математический маятник совершает гармонические колебания, если угол откло­нения нити от положения равновесия не превышает примерно 8^o.

«Песочный» маятник состоит из тяжелого тела М, подвешенного на двух нитях (бифилярный подвес), с воронкой для песка. С помощью муфты С, передвигаемой по нитям, можно реализовать различные соотношения периодов (частот) между склады­ваемыми колебаниями (рис.1а,б). В случае «а» муфта С дает возможность образовать два маятника: один из них имеет длину ДМ = l ₁ и может колебаться только в направле­нии оси у (одна степень свободы).

Маятник СМ с длиной l ₂ может совершать колебания относительно точки С в на­правлении х.

В случае «б» муфта С поднята и закреплена в точке Д так, что оба маятника име­ют одинаковые длины (l ₁ = l ₂) и могут совершать колебания в любом направлении.

Колеблющийся маятник в обоих случаях совершает движения, которые можно рассматривать как результат сложения колебаний по двум взаимно перпендикулярным направлениям.

Если в воронку насыпать песок и менять соотношение периодов складываемых колебаний (перемещать муфту С), то можно наблюдать различные фигуры – траектории, описываемые маятником, т.е. фигуры Лиссажу (рис.3). Фигура Лиссажу остается неиз­менной, если отношение периодов (частот) представляет собой рациональное число; в противном случае траектории не повторяются и фигура Лиссажу непрерывно изменяет­ся. Форма фигур Лиссажу зависит от отношения периодов (частот) и разности началь­ных фаз.

 

Порядок выполнения работы

1. Исследуйте форму траектории суммарного колебания при одинаковых периодах складываемых взаимно перпендикулярных колебаний. Определите параметры взаимно перпендикулярных колебаний (амплитуды а и b и частоту w). Настройте песочный ма­ятник так, чтобы складываемые колебания имели одинаковый период (Т₁ = Т₂), для чего нужно закрепить муфту С за крючок перекладины в точке Д (рис.1б).

Для исследования траектории положите под маятник лист бумаги. Отметьте на нем проекцию неподвижного маятника (точка О на листе бумаги) и проведите оси х, у. Отведите маятник с воронкой, заполненной песком, из положения равновесия вдоль оси х (или у) и сообщите ему импульс вдоль оси у (или оси х). Песка в воронку насыпать столько, чтобы хватило обозначить на бумаге получившуюся «песочную» фигуру, обве­дите ее карандашом.

Замечание: воронка располагается в непосредственной близости от поверхности листа бумаги, песок в воронку нужно сыпать после проведения всех дополнительных работ непосредственно перед наблюдением.

При заданных условиях возбуждения колебаний на листе бумаги получится тра­ектория движения маятника (эллипс) (рис.1в).

Найдите амплитуды а, b и разность фаз j, складываемых колебаний. Разность фаз j можно найти, положив в уравнении (4) х = 0 (или у = 0). В этом случае

.

2. Определите период колебания Т маятника. Для этого выведите маятник из положения равновесия и с помощью секундомера измерьте время t нескольких полных колебаний n маятника (например, n = 10), тогда 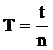. Выполнить задание, возбуждая колебания маятника сначала по оси ох, а затем по оси oy.

3. Результаты измерений и вычислений занести в таблицу.

Колебания в на­прав­лении	Число коле­баний, n	Время n колебаний, t,c	Т, с	w, с-1	а, м	b, м	j, град	j, рад	Уравнения колеба­ний в параметри­ческой форме
ox
oy

 

4. Напишите уравнение эллипса, используя полученные экспериментальные данные.

5. Рассчитайте, какие длины l ₁ и l ₂ должны быть у маятников, чтобы получить фигуру Лиссажу при условии T₁:T₂ = 1:2 (см. рис.3). Установите эти длины на песочном маятнике и проведите эксперимент, получив на том же листе бумаги (см. п.1) фигуру Лиссажу. Сравните ее с рис. 3.

 

Контрольные вопросы и упражнения

1. Что такое гармоническое колебание, и какими параметрами оно характеризуется?

2. От чего зависит траектория результирующего движения при сложении двух взаимно перпендикулярных колебаний?

3. Почему допустимо считать «песочный маятник» математическим?

4. Как вычисляются период и частота математического маятника?

Литература

1. Ремизов А.Н. Медицинская и биологическая физика. – М.: Высшая школа, 1999. – § 7.3.

2. Ливенцев. Курс общей физики. – М.: Высшая школа, 1974. – § 28.

3. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1997. – § 145.

4. Лаврова И.В. Курс физики. – М.: Просвещение, 1981. – § 54.

 

 

Лабораторная работа № 4