Цель работы: изучение статистических методов обработки опытных данных, подчиняющихся нормальному закону распределения случайных величин.
Приборы и принадлежности: микрометр, набор спичек.
Результат измерения физических величин зависит от многих факторов, влияние которых заранее учесть невозможно. Значения, полученные в результате прямых измерений какого-либо параметра, являются случайными. Если число измерений одного и того же параметра велико, то в значениях, принимаемых случайной величиной, обнаруживаются некоторые закономерности.
Пусть в n опытах измеряемая величина приняла m раз некоторое значение, тогда для этого значения отношение
 (1)
(1)
будет частотой события.
Сумма произведений всех значений случайной величины на их частоту называется средним арифметическим значением случайной величины (математическое ожидание дискретной случайной величины):
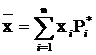 (2)
(2)
или
 .
.
При небольшом числе опытов частота событий в значительной мере имеет случайный характер и может заметно изменяться от одной группы опытов к другой. Однако при увеличении числа опытов частота событий теряет свой случайный характер и приближается к своей постоянной величине Р – статистической вероятности события:
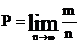 . (3)
. (3)
Например, при многократном бросании монеты частота выпадения герба будет лишь незначительно отличаться от 1/2.
Отклонение случайной величины от ее среднего значения характеризуется дисперсией, которая для опытных данных определяется формулой
 . (4)
. (4)
Для того чтобы оценивать рассеяние случайной величины в единицах той же размерности, вводят понятие среднего квадратичного отклонения:
 . (5)
. (5)
Всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, есть закон распределения случайной величины. Про случайную величину в этом случае говорят, что она подчиняется данному закону распределения. Закон распределения может быть задан в разных формах:
а) ряд распределения (для дискретных величин);
б) функция распределения;
в) кривая распределения (для непрерывных величин).
Простейшей формой является ряд распределения, который представляет собой таблицу значений случайных величин и соответствующих им частот.
 Существует множество законов распределения случайных величин. Одним из наиболее распространенных и общих является нормальный закон распределения [(см. (7)], характеризующийся тем, что для него среднее арифметическое значение случайной величины является также и наиболее вероятным.
Существует множество законов распределения случайных величин. Одним из наиболее распространенных и общих является нормальный закон распределения [(см. (7)], характеризующийся тем, что для него среднее арифметическое значение случайной величины является также и наиболее вероятным.
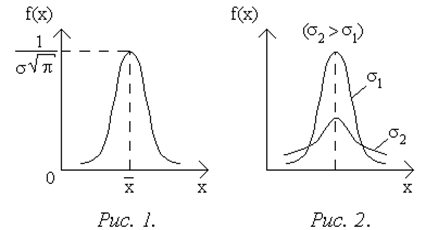
График нормального закона распределения изображен на рис.1. Кривая симметрична относительно прямой  , так как отклонения случайной величины вправо и влево от
, так как отклонения случайной величины вправо и влево от  равновероятны. При х ® ¥ кривая асимптотически приближается к оси абсцисс. Форма кривой распределения зависит от величины среднего квадратичного отклонения (рис.2).
равновероятны. При х ® ¥ кривая асимптотически приближается к оси абсцисс. Форма кривой распределения зависит от величины среднего квадратичного отклонения (рис.2).
Максимальное значение функция распределения вероятности принимает при  вид
вид
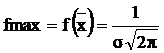 . (6)
. (6)
 Совокупность всех значений случайной величины называется простым статистическим рядом. Так как простой статистический ряд оказывается большим, его преобразуют в статистический ряд. Для этого весь диапазон измерения случайной величины делят на несколько равных интервалов и для каждого подсчитывают число m i значений случайной величины, попавших в этот интервал. После этого вычисляют частоту случайной величины
Совокупность всех значений случайной величины называется простым статистическим рядом. Так как простой статистический ряд оказывается большим, его преобразуют в статистический ряд. Для этого весь диапазон измерения случайной величины делят на несколько равных интервалов и для каждого подсчитывают число m i значений случайной величины, попавших в этот интервал. После этого вычисляют частоту случайной величины 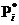 для каждого интервала Dх i и среднее значение случайной величины в каждом интервале
для каждого интервала Dх i и среднее значение случайной величины в каждом интервале  .
.
По статистическому ряду строится гистограмма. Для чего по оси абсцисс откладывают интервалы, являющиеся основаниями прямоугольников, высота которых равна  (рис.3). В том случае, если случайная величина распределена по нормальному закону, для построения кривой распределения находят значения функции распределения вероятностей при
(рис.3). В том случае, если случайная величина распределена по нормальному закону, для построения кривой распределения находят значения функции распределения вероятностей при  :
:
 . (7)
. (7)
Эту функцию можно представить в виде
 ,
,
где  . (8)
. (8)
Значения функции f0(Z i) приведены в таблице приложения.
Порядок выполнения работы
1. Измерьте с помощью микрометра диаметры х i 100 однородных спичек.
2. Результаты измерений занесите в таблицу (простой статистический ряд).
3. Составьте статистический ряд:
а) разбейте диапазон значений х i на 7–9 равных интервалов с границами
х i min и х i max;
б) рассчитайте  для каждого интервала;
для каждого интервала;
в) подсчитайте число m i значений диаметров, попавших в каждый интер-
вал;
г) по формуле  определите частоты, соответствующие каждому
определите частоты, соответствующие каждому
интервалу.
4. Найдите значение  для каждого интервала и постройте гистограмму.
для каждого интервала и постройте гистограмму.
5. Определите среднее арифметическое значение, дисперсию и среднее квадратичное отклонение [(см. (2, 4, 5)].
6. Вычислите функцию распределения вероятностей [см. (7, 8) и Приложение 3].
7. Постройте график функции  в одной системе координат с гистограммой. Максимум кривой соответствует
в одной системе координат с гистограммой. Максимум кривой соответствует 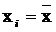 . Для нахождения ординаты этой точки следует определить f0(Z i) при
. Для нахождения ординаты этой точки следует определить f0(Z i) при 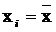 , т.е. f0(0) и вычислить f0(0) по Приложению 3.
, т.е. f0(0) и вычислить f0(0) по Приложению 3.
8. Результаты измерений и вычислений занесите в таблицу.
| х i max, мм
х i min, мм
| 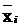 , мм , мм
| m i
| 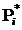
|  , мм-1 , мм-1
|  , мм , мм
| Z i, мм
| f0(Z i)
|  , мм , мм
|
|
|
|
|
|
|
|
|
|
|
9. Результаты измерений запишите в виде 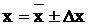 . Интервал Dх укажите с доверительной вероятностью a = 0,95.
. Интервал Dх укажите с доверительной вероятностью a = 0,95.
Вопросы
1. Что называется статистической вероятностью события?
2. Запишите формулу для определения математического ожидания и дисперсии случайной величины.
3. Перечислите способы задания закона распределения случайной величины.
4. Запишите функцию, соответствующую нормальному закону распределения случайной величины.
5. Укажите основные особенности нормального закона распределения случайной величины.
6. Укажите основные этапы построения гистограммы.
7. Как зависит форма кривой распределения от дисперсии случайной величины?
Лабораторная работа № 2
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛ МЕТОДОМ ТРИФИЛЯРНОГО ПОДВЕСА
Цель работы: измерение момента инерции тел правильной геометрической формы и момента инерции тела человека.
Приборы и принадлежности: трифилярный подвес, секундомер, штангенциркуль, набор тел правильной геометрической формы, модель тела человека.
ВНИМАНИЕ! m0 = 210 г, R = 11 см, r = 4,5 см, l = 41 см
Момент инерции материальной точки
 ,
,
где m – масса точки, r – расстояние от оси вращения.
Момент инерции тела относительно оси вращения
 .
.
Для сплошного тела
 . (1)
. (1)
Из формулы (1) видно, что момент инерции тел одинаковой массы, но различной конфигурации различен в зависимости от распределения массы относительно оси вращения.
В некоторых разделах космической и спортивной медицины, ортопедии, бионики возникает необходимость измерения момента инерции тела человека и отдельных его частей.
При беге, например, значительная часть энергии расходуется на то, чтобы придать конечностям ускорение, направленное поочередно то вперед, то назад. Чем больше момент инерции, тем больше требуется на это энергии. У человека мускулатура конечностей расположена главным образом в области плеча и бедра, а не по всей длине руки или ноги, в этом случае момент инерции является минимальным.
Определение момента инерции тела человека сложно, поэтому мы прибегнем к модели. Измерив момент инерции модели, можно, пользуясь теорией подобия, рассчитать момент инерции тела человека.
Подобными друг другу называются явления и тела, для которых одноименные параметры, характеризующие их, относятся между собой как постоянные числа. Рассмотрим основные положения теории подобия на примере момента инерции тела относительно оси.
Пусть моменты инерции двух подобных тел равны
 , (2)
, (2)
 . (3)
. (3)
По определению, подобия отношения всех величин, входящих в эти формулы, должны быть выражены постоянными числами, называемыми константами подобия:
 ,
, 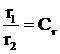 ,
, 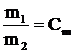 или
или  ,
,  ,
,  ,
,
где r1 и r2 – соответствующие линейные параметры двух тел, например, радиусы цилиндров. На основании этих соотношений и формулы (2) получаем
 ,
,
откуда
 . (4)
. (4)
Для выполнения равенства (4) необходимо, чтобы
 . (5)
. (5)
Величина  называется индикатором подобия, а равенство – условием подобия. У подобных явлений индикаторы подобия равны.
называется индикатором подобия, а равенство – условием подобия. У подобных явлений индикаторы подобия равны.
Из уравнений (4), (5) видно, что константы подобия не могут выбираться произвольно, они оказываются связанными уравнением (5). Подставляя константы подобия в уравнение (5), получаем
 ,
,
т.е.  одинаково для всех подобных явлений. Величина
одинаково для всех подобных явлений. Величина  называется инвариантом, или критерием подобия. У подобных явлений критерии численно равны. На основании подобия можно определить момент инерции тела человека с помощью модели, считая тело человека однородным. Зная соотношение Сm между массой человека и массой модели и соотношение Сr между линейными размерами человека и модели, можно определить
называется инвариантом, или критерием подобия. У подобных явлений критерии численно равны. На основании подобия можно определить момент инерции тела человека с помощью модели, считая тело человека однородным. Зная соотношение Сm между массой человека и массой модели и соотношение Сr между линейными размерами человека и модели, можно определить  . Измерив экспериментально момент инерции Im модели, можно определить момент инерции тела человека:
. Измерив экспериментально момент инерции Im модели, можно определить момент инерции тела человека:
 . (6)
. (6)
Описание установки
Рис. 1 Рис. 2
Трифилярный подвес представляет собой круглую платформу, которая крепится к диску тремя симметрично расположенными нитями (рис.1). Потянув за рычаг 1, выводят верхний диск из положения равновесия. Силовое воздействие по нитям будет передаваться нижнему диску.
Количество совершаемых диском крутильных колебаний можно подсчитать, наблюдая за меткой М, имеющейся на диске. Двигаясь в одном направлении, платформа поднимается на высоту h, при этом потенциальная энергия изменяется на mgh.
В момент прохождения положения равновесия потенциальная энергия платформы переходит в кинетическую:
 , (7)
, (7)
где I – момент инерции платформы; w – угловая скорость.
Если не учитывать силы трения, то колебания платформы можно считать гармоническими для малых амплитуд:
 ,
,
где а 0 – максимальный угол отклонения платформы; W – круговая частота колебаний платформы; Т – период колебаний. По определению, угловая скорость равна
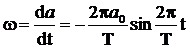 ,
,
где  . (8)
. (8)
Из рис.2 можно найти высоту, на которую поднимается платформа: h = h1 – h2. Так как
 и
и  ,
,
где l – длина нити подвеса, то
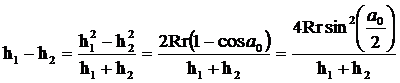 .
.
При небольших углах поворота можно считать, что
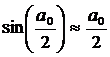 и
и  ,
,
тогда  . (9)
. (9)
Из соотношений (7–9) получаем
 . (10)
. (10)
Для того чтобы определить момент инерции любого тела, его помещают на платформу так, чтобы ось вращения проходила через геометрический центр платформы. Зная момент инерции пустой I0 и нагруженной Iн платформ, можно найти момент инерции тела:
 . (11)
. (11)
Порядок выполнения работы
1. Определение момента инерции пустой платформы:
а) потянув рычаг, сообщите платформе колебания (а 0 » 6о – 8о);
б) найдите с помощью секундомера время t0 полных n колебаний (возьмите n равным 10). Повторите опыт три раза;
в) найдите период  колебаний платформы;
колебаний платформы;
г) рассчитайте момент инерции 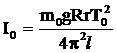 платформы и вычислите среднее
платформы и вычислите среднее  ;
;
д) результаты измерений и вычислений занесите в таблицу.
| t0, c
| T0, c
| I0, кг×м2
|  , кг×м2 , кг×м2
|
|
|
|
|
|
2. Определите момент инерции тела правильной формы:
а) поместите на платформу исследуемое тело так, чтобы не было перекоса платформы, и повторите действия а – б задания 1;
б) найдите период 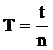 колебаний нагруженной платформы;
колебаний нагруженной платформы;
в) рассчитайте момент инерции  нагруженной платформы (m0 – масса платформы, R – радиус платформы, r – радиус верхнего диска, l – длина нитей подвеса. Значения m0, R, r, l указаны на первой странице описания;
нагруженной платформы (m0 – масса платформы, R – радиус платформы, r – радиус верхнего диска, l – длина нитей подвеса. Значения m0, R, r, l указаны на первой странице описания;
г) рассчитайте момент инерции тела Iт [см. (11)] и вычислите среднее  ;
;
д) результаты измерений занесите в таблицу.
| t, c
| Т, с
| Iн, кг×м2
| Iт, кг×м2
|  , кг×м2 , кг×м2
|
|
|
|
|
|
|
3. Определение момента инерции тела человека:
а) установите модель в центре платформы;
б) проведите измерения согласно заданию 2;
в) рассчитайте момент инерции модели;
г) рассчитайте момент инерции тела человека [см. (6)];
д) результаты измерений и вычислений занесите в таблицу, аналогичную таблице.
Контрольные вопросы
1. Что называется абсолютно твердым телом?
2. Дайте определение момента инерции материальной точки и тела относительно оси вращения.
3. Выведите формулу для кинетической энергии вращающегося тела.
4. Что представляет собой трифилярный подвес?
5. Какие явления называются подобными?
6. Что называется инвариантом подобия?
7. Как, используя теорию подобия, определить момент инерции тела человека?
Литература
1. Ремизов А.Н. Медицинская и биологическая физика. – М.: Высшая школа, 1999. – §5.2.
2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1997. – §§16, 17, 18.
3. Лаврова И.В. Курс физики. – М.: Просвещение, 1981. – §§10, 12.
Лабораторная работа № 3
СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ





 (1)
(1)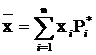 (2)
(2) .
.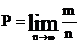 . (3)
. (3) . (4)
. (4) . (5)
. (5) Существует множество законов распределения случайных величин. Одним из наиболее распространенных и общих является нормальный закон распределения [(см. (7)], характеризующийся тем, что для него среднее арифметическое значение случайной величины является также и наиболее вероятным.
Существует множество законов распределения случайных величин. Одним из наиболее распространенных и общих является нормальный закон распределения [(см. (7)], характеризующийся тем, что для него среднее арифметическое значение случайной величины является также и наиболее вероятным. , так как отклонения случайной величины вправо и влево от
, так как отклонения случайной величины вправо и влево от  равновероятны. При х ® ¥ кривая асимптотически приближается к оси абсцисс. Форма кривой распределения зависит от величины среднего квадратичного отклонения (рис.2).
равновероятны. При х ® ¥ кривая асимптотически приближается к оси абсцисс. Форма кривой распределения зависит от величины среднего квадратичного отклонения (рис.2).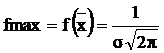 . (6)
. (6) Совокупность всех значений случайной величины называется простым статистическим рядом. Так как простой статистический ряд оказывается большим, его преобразуют в статистический ряд. Для этого весь диапазон измерения случайной величины делят на несколько равных интервалов и для каждого подсчитывают число m i значений случайной величины, попавших в этот интервал. После этого вычисляют частоту случайной величины
Совокупность всех значений случайной величины называется простым статистическим рядом. Так как простой статистический ряд оказывается большим, его преобразуют в статистический ряд. Для этого весь диапазон измерения случайной величины делят на несколько равных интервалов и для каждого подсчитывают число m i значений случайной величины, попавших в этот интервал. После этого вычисляют частоту случайной величины 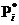 для каждого интервала Dх i и среднее значение случайной величины в каждом интервале
для каждого интервала Dх i и среднее значение случайной величины в каждом интервале  .
. (рис.3). В том случае, если случайная величина распределена по нормальному закону, для построения кривой распределения находят значения функции распределения вероятностей при
(рис.3). В том случае, если случайная величина распределена по нормальному закону, для построения кривой распределения находят значения функции распределения вероятностей при  :
: . (7)
. (7) ,
, . (8)
. (8) для каждого интервала;
для каждого интервала; определите частоты, соответствующие каждому
определите частоты, соответствующие каждому в одной системе координат с гистограммой. Максимум кривой соответствует
в одной системе координат с гистограммой. Максимум кривой соответствует 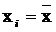 . Для нахождения ординаты этой точки следует определить f0(Z i) при
. Для нахождения ординаты этой точки следует определить f0(Z i) при 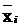 , мм
, мм
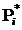
 , мм
, мм
 , мм
, мм
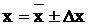 . Интервал Dх укажите с доверительной вероятностью a = 0,95.
. Интервал Dх укажите с доверительной вероятностью a = 0,95. ,
, .
. . (1)
. (1) , (2)
, (2) . (3)
. (3) ,
, 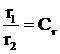 ,
, 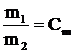 или
или  ,
,  ,
,  ,
, ,
, . (4)
. (4) . (5)
. (5) называется индикатором подобия, а равенство – условием подобия. У подобных явлений индикаторы подобия равны.
называется индикатором подобия, а равенство – условием подобия. У подобных явлений индикаторы подобия равны. ,
, одинаково для всех подобных явлений. Величина
одинаково для всех подобных явлений. Величина  называется инвариантом, или критерием подобия. У подобных явлений критерии численно равны. На основании подобия можно определить момент инерции тела человека с помощью модели, считая тело человека однородным. Зная соотношение Сm между массой человека и массой модели и соотношение Сr между линейными размерами человека и модели, можно определить
называется инвариантом, или критерием подобия. У подобных явлений критерии численно равны. На основании подобия можно определить момент инерции тела человека с помощью модели, считая тело человека однородным. Зная соотношение Сm между массой человека и массой модели и соотношение Сr между линейными размерами человека и модели, можно определить  . Измерив экспериментально момент инерции Im модели, можно определить момент инерции тела человека:
. Измерив экспериментально момент инерции Im модели, можно определить момент инерции тела человека: . (6)
. (6)
 , (7)
, (7) ,
,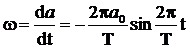 ,
, . (8)
. (8) и
и  ,
,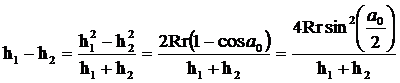 .
.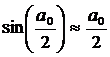 и
и  ,
, . (9)
. (9) . (10)
. (10) . (11)
. (11) колебаний платформы;
колебаний платформы;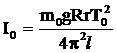 платформы и вычислите среднее
платформы и вычислите среднее  ;
;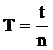 колебаний нагруженной платформы;
колебаний нагруженной платформы; нагруженной платформы (m0 – масса платформы, R – радиус платформы, r – радиус верхнего диска, l – длина нитей подвеса. Значения m0, R, r, l указаны на первой странице описания;
нагруженной платформы (m0 – масса платформы, R – радиус платформы, r – радиус верхнего диска, l – длина нитей подвеса. Значения m0, R, r, l указаны на первой странице описания; ;
;
