Рассмотрим плоскую фигуру площадью А и ограниченную некоторой кривой (рис. 7.7) в прямоугольной системе координат. Примем плотность тела  , т.е. тогда масса любой части тела будет измеряться ее площадью. Это всегда подразумевается, когда говорят о статических моментах. Выделим в плоскости фигуры элемент площади dA с координатами х и у (pис. 7.7) и определим статические моменты плоской фигуры, как взятые по всей площади А суммы произведений элементарных площадей dA на их расстояния х и у до осей Ох и Оу. Итак, статические моменты плоской фигуры определяются как
, т.е. тогда масса любой части тела будет измеряться ее площадью. Это всегда подразумевается, когда говорят о статических моментах. Выделим в плоскости фигуры элемент площади dA с координатами х и у (pис. 7.7) и определим статические моменты плоской фигуры, как взятые по всей площади А суммы произведений элементарных площадей dA на их расстояния х и у до осей Ох и Оу. Итак, статические моменты плоской фигуры определяются как
 . (7.9)
. (7.9)

Рис. 7.7
Статические моменты обычно выражаются в см 3 или м 3.
При параллельном переносе осей значения статических моментов не остаются постоянными, а изменяются и могут иметь как положительное, так и отрицательное значение. Следовательно, существует ось, относительно которой статический момент равен нулю.
Ось, относительно которой статический момент равен нулю, называется центральной.
Точка пересечения центральных осей является центром тяжести сечения.
Если известны статические моменты площади фигуры относительно координатных осей, то координаты ее центра тяжести можно определить по формулам
 , (7.10)
, (7.10)
где А - площадь сечения.
Пример 3. Вычислить центр тяжести плоской фигуры, изображенной на рис. 7.8. Размеры сечения на рисунке даны в сантиметрах.


Рис. 7.8
Решение. Сечение имеет ось симметрии. Поэтому определяем только координату 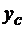 пользуясь методом разбиения на части. Дополним трапецию до треугольника abf uрассмотрим заданное сечение, состоящее из треугольников abf (часть 1) и def (часть 2) (рис. 7.8). При вычислении статического момента площадь треугольника def следует брать со знаком «минус», так как этот треугольник является дополнением к заданному сечению (трапеции).
пользуясь методом разбиения на части. Дополним трапецию до треугольника abf uрассмотрим заданное сечение, состоящее из треугольников abf (часть 1) и def (часть 2) (рис. 7.8). При вычислении статического момента площадь треугольника def следует брать со знаком «минус», так как этот треугольник является дополнением к заданному сечению (трапеции).
Вычислим центр тяжести по формулам (7.9).
Определим статический момент трапеции относительно оси Ох.

 .
.
Площадь сечения
 .
.
Тогда
 .
.
Статический момент  можно также определить как сумму статических моментов составляющих ее частей относительно той же оси Ох. Для этого разобьем трапецию на два одинаковых треугольника amd (часть 1) и пbе (часть 2) и прямоугольник mden (часть 3) (рис. 7.8, б) и вычислим
можно также определить как сумму статических моментов составляющих ее частей относительно той же оси Ох. Для этого разобьем трапецию на два одинаковых треугольника amd (часть 1) и пbе (часть 2) и прямоугольник mden (часть 3) (рис. 7.8, б) и вычислим

Координата центра тяжести 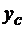 имеет положительное значение, т. к.
имеет положительное значение, т. к.  и, следовательно, должна быть отложена по оси Оу вверх.
и, следовательно, должна быть отложена по оси Оу вверх.
6 Вспомогательные теоремы для определения
Положения центра тяжести
При вычислении координат центров тяжести пользуются различными приемами, позволяющими упростить вычисления. Рассмотрим четыре вспомогательные теоремы, упрощающие в некоторых случаях нахождение центров тяжести.
Теорема 1. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
Теорема 2. Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости.
На основе рассмотренных теорем можно определить положения центров тяжести некоторых симметричных линий, фигур и тел:
1) центр тяжести отрезка прямой лежит в его середине;
2) центры тяжести окружности, площади круга, поверхности и объема шара находятся в их геометрических центрах;
3) центры тяжести периметра и площади параллелограмма, ромба, прямоугольника и квадрата лежат в точках пересечения их диагоналей;
4) центр тяжести периметра и площади правильного многоугольника находится в центре вписанного (или описанного) круга.
Теорема 3. Объем тела вращения, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описаннойее центром тяжести.
Пусть плоская фигура площадью F вращается вокруг оси у, лежащей в плоскости фигуры и не пересекающей ее. При вращении вокруг оси у контур этой фигуры описывает некоторую замкнутую поверхность, называемую поверхностью вращения. Тело, ограниченное этой поверхностью, называется телом вращения (рис. 7.9). Объем этого тела вращения определим как сумму бесконечно большого числа объемов элементарных круговых колец, образованных вращением вокруг оси у бесконечно малых площадок Δ F i. Радиус каждого кольца равен расстоянию этой площади от оси у, т. е. координате x i.
Объем элементарного кольца
 .
.
Объем тела вращения
 .
.
Здесь суммирование распространено на все площадки, входящие в состав данной площади F.
Сумму  можно определить из формулы:
можно определить из формулы:
 .
.
Подставив это значение в выражение, определяющее объем тела вращения, получим
 . (7.11)
. (7.11)
где 2 πхс - длина окружности, описанной центром тяжести фигуры.


Рис. 7.9 Рис. 7.10
Теорема 4. Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но не пересекающей ее, равна произведению длины этой кривой на длину окружности, описанной ее центрам тяжести.
Пусть кривая АВ длиной L вращается вокруг оси у, лежащей в плоскости этой кривой, но не пересекающей ее. При вращения вокруг оси у эта кривая опишет некоторую поверхность вращения (рис. 7.10).
Разобьем кривую на бесчисленное множество бесконечно малых элементов длиной Δ li. Поверхность, описанную каждым элементом, можно принять за поверхность усеченного конуса.
Как известноиз геометрии, площадь боковой поверхности усеченного конуса равна произведению длины окружности среднего сечения на длину образующей. Поэтому площадь поверхности, образованной вращением элемента кривой Δ li, можно определить по формуле
 ,
,
где х i - радиус окружности, равный расстоянию серединыэлементаот оси у.
Площадь поверхности вращения
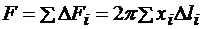 ,
,
здесь суммирование распространено на все элементы Δ l i кривой АВ. Сумму  определим из формулы:
определим из формулы:
 .
.
Подставив это значение в выражение, определяющее площадь поверхности вращения, получим
 .
.
Таблица 7.1
Центры тяжести некоторых фигур
| Центр тяжести
| Рисунок
| Формула
|
|
Центр тяжести площади треугольника
| 
|
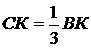
|
|
Центр тяжести площади трапеции
| 
|

|
|
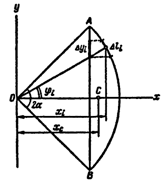
Центр тяжести дуги окружности
| 
|

|
|
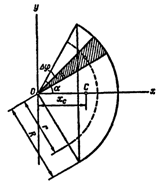
Центр тяжести площади сектора круга
| 
|

|
|
Центр тяжести объема пирамиды
| 
|

|
|
Центр тяжести объема конуса
| 
|

|
Раздел 2 Кинематика
Лекция 8
КИНЕМАТИКА ТОЧКИ
ПРЕДМЕТ И ЗАДАЧИ КИНЕМАТИКИ
Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел. Движущиеся тала рассматриваются как чисто геометрические объекты - и тела – без учета их материальных характеристик (массы и др.). При этом не рассматриваются причины (действующие на тела силы), вызывающие и изменяющие движение объекта.
Под движением в механике понимается изменение с течением времени положения в пространстве данного тела по отношению к какому-либо другому телу. Характер наблюдаемого движения существенно зависит от выбора тела, с которым связан наблюдатель. С твердым телом, по отношению к которому изучается движение, жестко соединяют какую-нибудь систему координат, образующую вместе с этим телом систему отсчета. Пространство в механике рассматривается как трехмерное эвклидово. Время считается универсальным, т. е. протекающим одинаково во всех рассматриваемых системах отсчета. В задачах кинематики время (скалярная непрерывно изменяющаяся величина) принимается за независимое переменное (аргумент). Отсчет времени ведется от некоторого условного начального момента, о выборе которого в каждом случае условливаются. меняющаяся величина. За единицу времени принимается одна секунда, равная 1/(24*3600) средних солнечных суток.
Все кинематические величины, характеризующие движение твердого тела и движение отдельной его точки (расстояния, скорости, ускорения и т. д.), рассматриваются как функции времени.
Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано.
Кинематически задать движение тела (точки) – значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени. Если положение тела (точки) определяется какими-либо координатами (параметрами), то надо задать зависимость от времени t. Такая зависимость называется кинематическими уравнениями движения или законом движения.
Основной задачей кинематики является установления математических способов задания движения тела (точки) и методов определения всех кинематических величин, характеризующих данное движение.
Движение точки считается заданным, если указан способ, позволяющий определить положение точки в каждый момент времени относительно выбранной системы отсчета. Существует три способа задания движения точки: 1) векторный; 2) координатный; 3) естественный. Векторный способ применяется главным образом при исследовании теоретических вопросов, а координатный и естественный употребляются преимущественно при решении различных практических задач.
Теперь последовательно разберем эти три способа задания движения точки.
СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
Векторный способ задания движения точки
Положение точки в пространстве однозначно определяется заданием радиуса-вектора 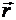 , проведенногоиз некоторого неподвижного центра О в данную точку М (рис. 8.1).
, проведенногоиз некоторого неподвижного центра О в данную точку М (рис. 8.1).

Рис. 8.1
Траектория точки является геометрическим местом концов радиуса-вектора 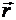 движущейся точки.
движущейся точки.
Линия, образованная концами переменного вектора, начало которого находится в определенной точке пространства, называется годографом этого вектора.
Для определения движения точки нужно знать, как изменяется с течением времени радиус-вектор 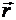 , т. е. должна быть задана вектор-функция
, т. е. должна быть задана вектор-функция 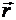 аргумента t:
аргумента t:
 (8.1)
(8.1)
Следовательно, траектория точки М является годографом ее радиуса-вектора 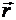 .
.
Векторный способ определения движения материальной точки или системы материальных точек широко используется и в кинематике, и в динамике, так как он значительно упрощает многие выводы и иногда подчеркивает физическую сущность явлений. От векторных формул легко перейти к аналитическим выражениям, обычно более удобным для вычислений.
Координатный способ задания движения
Положение точки М в системе отсчета Охуz определяется тремя декартовыми координатами точки х, у, z (рис. 8.2). При движении точки М ее координаты изменяются с течением времени. Следовательно, координаты х, у, z движущейся точки М являются функциями времени t:
 . (8.2)
. (8.2)
Эти уравнения называются уравнениями движения точки в декартовых координатах.

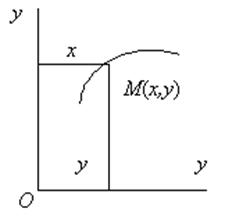
Рис. 8.2 Рис. 8.3

Рис. 8.4
Уравнениями (8.2) определяется движение точки.
Движение точки М в одной плоскости определяется двумя уравнениями движения (рис. 8.3):
 . (8.3)
. (8.3)
Прямолинейное движение точки М (рис. 8.4) определяется одним уравнением движения:
 . (8.4)
. (8.4)
Уравнения движения, определяющие координаты точки в любой момент времени, можно рассматриватькак параметрические уравнения траектории точки. При исключении параметра t из уравнений движения получаются уравнения траектории точки в координатной форме.
Пусть уравнения движения точки М имеют вид
 .
.
Решив первое уравнение относительно t, получим
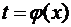 .
.
Подставив полученное для t выражение в два других уравнения, найдем уравнения траектории точки в координатной форме:

Как известно из аналитической геометрии, линии в пространстве соответствуют два уравнения с тремя координатами. Пусть движение точки М в плоскости задано уравнениями
 .
.
Исключив параметр t, получим уравнение траектории точки в координатной форме:
 .
.
Помимо декартовых координат для определения положения точки на плоскости и в пространстве применяют и другие системы координат (полярные, цилиндрические, сферические и др.).
Естественный способ задания движения точки
Рассмотрим естественный способ задания движения точки, применяемый в случае, когда траектория точки заранее известна. Траекторией может быть как прямая, так и кривая линия (рис. 8.5).


Рис. 8.5
Выберем на траектории неподвижную точку О, которую назовем началом отсчета дуговой координаты. Положение движущейся точки М на траектории будем определять дуговой координатой, т. е. расстоянием ОМ = s, отложенным по траектории от начала отсчета О.
Расстояния, отложенные в одну сторону от точки О, будем считать положительными, а в противоположную - отрицательными, т. е. установим направление отсчета дуговой координаты.
При движении точки М расстояние s от этой точки до неподвижной точки Оизменяется с течением времени, т. е. дуговая координата s является функцией времени:
 . (8.5)
. (8.5)
Эта зависимость называется уравнением движения точки.
Если вид функции f (t) известен, то для каждого значения t можно найти значение s, отложить соответствующее расстояние по траектории и указать, где находится движущаяся точка М в этот момент времени.
Таким образом, движение точки определено, если известны следующие элементы: траектория точки, начало и направление отсчета дуговой координаты и уравнение движения s = f (t).
Дуговую координату точки не следует смешивать с длиной пути σ, пройденного движущейся точкой. Дуговая координата s точки М в некоторый момент времени t может быть равна пути σ, пройденному точкой за промежуток времени [0, t ], только в том случае, если движение точки начинается из точки О и совершается в положительном направлении.
 .
.



 , т.е. тогда масса любой части тела будет измеряться ее площадью. Это всегда подразумевается, когда говорят о статических моментах. Выделим в плоскости фигуры элемент площади dA с координатами х и у (pис. 7.7) и определим статические моменты плоской фигуры, как взятые по всей площади А суммы произведений элементарных площадей dA на их расстояния х и у до осей Ох и Оу. Итак, статические моменты плоской фигуры определяются как
, т.е. тогда масса любой части тела будет измеряться ее площадью. Это всегда подразумевается, когда говорят о статических моментах. Выделим в плоскости фигуры элемент площади dA с координатами х и у (pис. 7.7) и определим статические моменты плоской фигуры, как взятые по всей площади А суммы произведений элементарных площадей dA на их расстояния х и у до осей Ох и Оу. Итак, статические моменты плоской фигуры определяются как . (7.9)
. (7.9)
 , (7.10)
, (7.10)

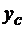 пользуясь методом разбиения на части. Дополним трапецию до треугольника abf uрассмотрим заданное сечение, состоящее из треугольников abf (часть 1) и def (часть 2) (рис. 7.8). При вычислении статического момента площадь треугольника def следует брать со знаком «минус», так как этот треугольник является дополнением к заданному сечению (трапеции).
пользуясь методом разбиения на части. Дополним трапецию до треугольника abf uрассмотрим заданное сечение, состоящее из треугольников abf (часть 1) и def (часть 2) (рис. 7.8). При вычислении статического момента площадь треугольника def следует брать со знаком «минус», так как этот треугольник является дополнением к заданному сечению (трапеции).
 .
. .
. .
. можно также определить как сумму статических моментов составляющих ее частей относительно той же оси Ох. Для этого разобьем трапецию на два одинаковых треугольника amd (часть 1) и пbе (часть 2) и прямоугольник mden (часть 3) (рис. 7.8, б) и вычислим
можно также определить как сумму статических моментов составляющих ее частей относительно той же оси Ох. Для этого разобьем трапецию на два одинаковых треугольника amd (часть 1) и пbе (часть 2) и прямоугольник mden (часть 3) (рис. 7.8, б) и вычислим
 и, следовательно, должна быть отложена по оси Оу вверх.
и, следовательно, должна быть отложена по оси Оу вверх. .
. .
. можно определить из формулы:
можно определить из формулы: .
. . (7.11)
. (7.11)

 ,
,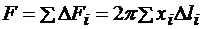 ,
, определим из формулы:
определим из формулы: .
. .
.
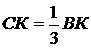










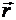 , проведенногоиз некоторого неподвижного центра О в данную точку М (рис. 8.1).
, проведенногоиз некоторого неподвижного центра О в данную точку М (рис. 8.1).
 (8.1)
(8.1) . (8.2)
. (8.2)


 . (8.3)
. (8.3) . (8.4)
. (8.4) .
.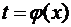 .
.
 .
. .
.

 . (8.5)
. (8.5) .
.

