

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Оснащения врачебно-сестринской бригады.
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
правило подстановки: если a — выводимая формула, содержащая букву A (обозначив это как a(A)), то выводима формула a(b), получающаяся из a заменой всех вхождений A на произвольную формулу b
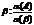 |
правило заключения (modus ponens): (если a ® b и a — выводимые формулы, то b также выводимая формула)
 |
Выводимость формул
Если формулы F 1, …, Fn, G находятся в отношении R, то формула G называется непосредственно выводимой из F 1, …, Fn по правилу R. формулы F 1, …, Fn, называются посылками правила R, а G — его следствием или заключением.
Выводом в T формулы Gиз формул A 1, …, An, называется всякая последовательность F 1, F 2,..., Fm формул такая, что Fm = G, а для любого i формула Fi есть либо аксиома теории T, либо одна из исходных формул A 1, …, An, либо выводима из формул F 1, …, Fi -1 по одному из правил вывода.
Если существует вывод Gиз A 1, …, An, то говорят, что G выводима из A 1, …, An т.е. является теоремой формальной теории Т. Этот факт обозначается A 1, …, An |— G.
Формулы A 1, …, An называются гипотезами или посылками вывода. Переход в выводе от Fi -1 к Fi называется i -м шагом вывода.
Разрешимые и неразрешимые формулы
В общем случае может не существовать эффективной процедуры, с помощью которой можно определить по данной формуле, существует ли ее вывод в теории T.
Формула, для которой такая процедура существует, называется разрешимой в этой теории, в противном случае — неразрешимой.
Иначе говоря, для неразрешимых формул нельзя построить алгоритм, который ответит на вопрос: является ли формула теоремой.
Полнота. Имеют место следующие метатеоремы.
Теорема 1: Всякая теорема исчисления высказываний (Т) есть тавтология (т.е. тождественно истинная формула)
Теорема 2: Всякая тавтология является теоремой исчисления высказываний.
Таким образом, теоремами теории Тявляются тождественно истинные формулы и только они.
Формальная теория Т (исчисление высказываний) является полной теорией
Непротиворечивость
Из теоремы 1 следует, что теория Тнепротиворечива.
Действительно, любая теорема в Тесть тождественно истинная
формула (тавтология). Ее отрицание не есть тавтология. Таким
образом в Тнет одновременной выводимости теоремы и ее
отрицания, что соответствует определению непротиворечивости
формальной теории.
Разрешимость
Теория Тразрешима как формальная теория.
Алгоритм, который определяет для любой формулы теории,
является ли эта формула теоремой теории, может состоять в
вычислении истинностных значений формулы в каждой
|
|
интерпретации. Принципиально это выполнимо за конечное время в
силу конечности числа интерпретаций и числа операций,
присутствующих в формуле.
58.Предикат: n -местный (n= 0, n >0). Предикатные формулы. Связь между предикатами, отношениями и функциями. Модель в логике предикатов.
Предикат – повествовательное предложение, содержащее предметные переменные xi ÎMi, определенные на соответствующих множествах Mi
Например: P(x,y)=«Студент x на экзамене получил отметку y». Переменные x, y являются предметными и принадлежат следующим множествам x={Иванов, Петров, Сидоров}, y={2,3,4,5}.
При замене переменных конкретными значениями (элементами множеств) предикат обращается в высказывание т.е. принимает значение «истинно» или «ложно». Например: «Студент Иванов на экзамене получил отметку 5»
Предикатом P (x 1, …, xn) зависящим от n переменных называется функция P: M 1 ´ M 2 ´…´ Mn ® B, где xi ÎMi произвольным множествам, а B — двоичное множество.
M 1, M 2, …, Mn – предметные области предиката, x 1, …, xn – предметные переменные предиката.
Алфавит алгебры предикатов
m-местная предикатная переменная — выражения вида P(x1..xm), где x1..xm предметные переменные
Логические символы &, Ú, ®, ~, Ø, $ (квантор существования), " (квантор всеобщности);
Вспомогательные символы (),
0-местные предикатные переменные (пропозициональные переменные) - выражения вида P(а1..аm), где а1..аm предметные константы.
Элементарной формулой называется всякая пропозициональная переменная, а также любая m -местная предикатная переменная (m > 0).
Из элементарных формул строятся предикатные формулы:
Все элементарные формулы суть формулы;
Если А и В — формулы, то выражения (А & В), (А Ú В), (А ® В), (А ~ В), ØА считаются формулами;
если А — формула, x — предметная переменная, то " x А и $ x В суть формулы.
Предикат тождества E(x1,x2): N 2 ® B: E (a 1, a 2) = 1 тогда и только тогда, когда a 1 = a 2, xi ÎN
Предикат порядка Q (x1,x2): N 2 ® B: Q (a 1, a 2) = 1 тогда и только тогда, когда a 1 £ a 2, xi ÎN
|
|
Предикат делимости D (x1,x2): N 2 ® B: D (a 1, a 2) = 1 тогда и только тогда, когда a 1 делится на a 2, xi ÎN
Предикат суммы S (x1,x2,x3): N 3 ® B: S (a 1, a 2, a 3) = 1 тогда и только тогда, когда a 1 + a 2 = a 3, xi ÎN
Предикат произведения P (x1,x2,x3): N 3 ® B: P (a 1, a 2, a 3) = 1 тогда и только тогда, когда a 1 * a 2 = a 3, xi ÎN
Для любых Мi, где i=1...n существует взаимнооднозначное соответствие между n –местным отношением R Í M 1 ´ M 2 ´…´ Mn и n –местным предикатом P: M 1 ´ M 2 ´…´ Mn ® B:
Каждому n –местному отношению R соответствует предикат P такой, что P (a 1, …, an) = 1, если и только если (a 1, …, an) Î R; При этом R задает область истинности предиката P.
Всякий предикат P (x 1, …, xn) определяет отношение R такое, что (a 1, …, an) Î R, если и только если P (a 1, …, an) = 1.
Пример: 2-местному предикату тождества Е:«х1=х2» взаимнооднозначно соответствует 2-месное отношение R1- «быть равным»: (а1,а2) Î R тогда и только тогда, когда Е(а1,а2)=1
|
|
|

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!