Отображения. Изоморфизм. Автоморфизм. Гомоморфизм. Эпиморфизм. Эндоморфизм. Мономорфизм. Биморфизм.

Гомоморфизм ГОМОМОРФИЗМ – отображение множества элементов одной алгебраической системы в другую, сохраняющее все отношения и операции

Даны A=<M1; φ>, B=<M2;ψ> и соответствие G отображает M1® M2.

Соответствие G - гомоморфизм алгебры А в алгебру В если

G (а φ b) = G(а) ψ G(b)

Над элементами а и b Î M1 выполняем операцию φ: a φ b = c

2) Результат операции с отображаем в множество M2: Г: с ®γ

3) Выполняет отображение элемента a в множество M2: Г: a ®α

4) Выполняет отображение элемента b в множество M2: Г: b ®β

5) Над элементами α и β Î M2 выполняем операциюψ: α ψ β = γ1

6) Если γ= γ1 то соответсвие гомоморфно, нет в противном случае.

Гомоморфизм? – пример проверки

Дано: A=<Z; “*”>, <Z; “*” > и отображение Г: n ® -n. Определить является ли данное соответствие гомоморфизмом

1) Над элементами а и b Î M1выполняем операцию φ: a φ b = c

т.е. a*b=c

2) Результат операции с отображаем в множество M2: Г: с ®γ

т.е. c ® -c=-ab и γ=-ab

3) Выполняет отображение элемента a в множество M2: Г: a ®α

т.е. a ® -a и α=-а

4) Выполняет отображение элемента b в множество M2: Г: b ®β

т.е. b ® -b и β=-b

5) Над элементами α и β Î M2 выполняем операцию ψ: α ψ β = γ1

т.е. α * β = ( -a)*(-b) = ab = γ1

6) Если γ= γ1 то отображение гомоморфно,

Т.е. ab ≠-ab не гомоморфно

 

Данны A=<Z; “*”>, <Z; “*” > и отображение Г: n ® -n. Определить является ли отображение всюду определенным, сюръективным, инъективным, функциональным?

A=<Z; “*”>, <Z; “*” > Г: n ® -n, каждый элемент первой алгебры имеет свой образ – всюду определенное

А=<Z; “*”>, <Z; “*” > Г: n ® -n, каждый элемент второй алгебры имеет свой прообраз – сюръективное

А=<Z; “*”>, <Z; “*” > Г: n ® -n, каждый элемент первой алгебры имеет единственный образ – функциональное

А=<Z; “*”>, <Z; “*” > Г: n ® -n, каждый элемент второй алгебры имеет единственный прообраз – инъективное

Типы морфизмов

Мономорфизм – это гомоморфное и инъективное соответствие

Эпиморфизм – это гомоморфное и сюръективное соответствие

Эндоморфизм – это гомоморфное соответствие и множество В=А

Биморфизм – это гомоморфное, биъективное соответствие

Изоморфизм - это гомоморфное и взаимооднозначное соответствие

Автоморфизм - это гомоморфное, взаимооднозначное соответствие и множество В=А

Изоморфизм

ИЗОМОРФИЗМ – это одно из основных понятий современной математики, которое исторически возникло сначала в пределах алгебры в применении к таким алгебраическим системам, как группы, кольца, поля и др.. Впоследствии оказалось принципиально существенным для общего понимания строения и структуры самых разных систем.

Пусть даны два множества S и S^/, причем в первом S определены отношения F_k (x ₁, x ₂,...), k = 1, 2,..., n, а во втором S^/ –отношения F^/_k (x^/ ₁, x^/ ₂,...), k = 1, 2,..., n. Множества S и S^/ с указанными отношениями называются изоморфными, если между ними существует такое взаимно однозначное соответствие x^/ =Г1(x), x = Г2(x^/), где x Î S, а x^/ Î S^/, что из наличия F_k (x ₁, x ₂,...) вытекает наличие F^/_k (x^/ ₁, x^/ ₂,...), и наоборот.

Отображение Г1 - изоморфное отображение или изоморфизмом системы S на систему S^/, а обратное ему отображение

Г2 – изоморфизмом системы S^/, на систему S.

Факт изоморфности систем S и S^/ обозначается S @ S ^/.

47.Логическое представление исследуемой системы. Простые и сложные высказывания. Логические операции. Таблица истинности и таблица Кэли. Конверсия, инверсия, контрапозиция. Необходимое, достаточное, необходимое и достаточное условие.???

Логические представления

Логические (формальные) представления исследуемой системы — это ее описание в виде совокупности сложных высказываний, составленных из простых (элементарных) высказываний и логических связок между ними.

Логические представления характеризуются определенными свойствами и набором допустимых преобразований над ними (операций, правил вывода и т.п.), которые являются правильными методами рассуждений — законами логики.

Предмет изучения

Способы (правила) формального логического представления высказываний, построения новых высказываний из имеющихся с помощью логически выдержанных преобразований

Способы (методы) установления истинности или ложности высказываний.

Высказывание — повествовательное предложение (утверждение, суждение), о котором имеет смысл говорить, что оно истинно или ложно. Пример: «Дважды два четыре», «На улице жара».

Все научные знания, события повседневной жизни, ситуации в

экономике, управлении, политике формируются в виде

высказываний.

Простые высказывания рассматриваются в данном контексте как неделимое целое (аналогично элементу множества)

Сложные высказывания формулируются из простых с помощью логических связок (логических операций), заменяющие связки естественного языка в сложных предложениях.

Логическая операция - это функция вида f(x1,x2,…xn): Bⁿ→B, где В множество состоящее из двух элементов В={0,1}.

Логическая операция – это функция зависящая от логических переменных (т.е. принимающих значение 0,1), которая так же может принимать только два значения 0 и 1.

В таблице истинности для бинарных операций первые два столбца содержат все возможные наборы операндов, а последующие столбцы значение логических функций.

Конъюнкция ( операция логического умножения, обозначается любым из символов А&В, А ÙВ, АВ) соответствует связывающему слову «И», «НО», «А». Значение операции А&B=1если оба операнда равны 1. Пример: «Дискретная математика легкий, но объемный предмет»

Дизъюнкция (операция логического сложения обозначается АÚВ) соответствует связывающему слову «ИЛИ». Подразумевает истинность А или В или обоих высказываний. Значение АÚВ=1 если хотя бы один из операндов равен 1. Пример: «Петров любит футбол или формулу-1»

Отрицание (операция отрицания или дополнения, обозначается любым из символовù А, Ā) соответствует связывающему слову «не верно, что» или «не …». Значение Ā=1 если А=0 и наоборот.

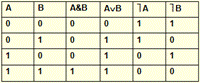
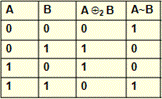
Разделительное ИЛИ (обозначается ХОR, Å ₂) соответствует фразам «ИЛИ», «Либо … либо» в разделительном смысле. Значение А Å ₂ В =1 если значение операндов различно. Например: «Студент Иванов сдаст экзамен по дискретной математике или не сдаст».

Эквивалентность (обозначается А~В) соответствует связкам «А эквивалентно В», «А равносильно В», «А тоже, что и В», «А тогда и только тогда, когда В», «А необходимо и достаточно для В». Значение А~В=1, Если А=В. Например: «Деление числа k на 2 и 3 (А) необходимо и достаточно для деления k на 6 (В)».

«Любое число делится на 6 (А) тогда и только тогда, когда оно делится на 2 и 3 (В)».

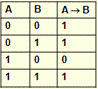
Условные высказывания типа «если А, то В», «А влечет В» соответствуют логической операции импликация. Обозначается следующим образом А®В. Пример: отец говорит сыну: «Если в этом семестре ты сдашь все экзамены на «отлично» (A), то я куплю тебе машину (B)». При каких условиях отец говорит правду?