Таблицы истинности сложных функций

Таблицы истинности для сложных функций строится поэтапно, путем выделения простых функций согласно последовательности их выполнения

Таблица истинности для формулы

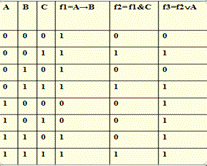
F= ((А→В)&C) Ú A

Тождественно Истинная, Тождественно Ложная и Выполнимая формула

Формула называется тождественно истинной (общезначимой, тавтологией), если при всех возможных наборах переменных формула равна 1

Формула называется тождественно ложной (противоречием), если при всех возможных наборах переменных формула равна 0

Формула называется выполнимой, если при некоторых наборах переменных формула равна 1. При этом,

Единичным набором переменных называется набор переменных, при которых функция равна 1. Множество единичных наборов называется единичным множеством

Нулевым набором переменных называется набор переменных, при которых функция равна 0. Множество нулевых наборов называется нулевым множеством

51.Формы записи формул (функций) — инфиксная, префиксная, постфиксная. Преобразования формул: инфиксная в префиксную и постфиксную, префиксная в инфиксную, постфиксная в инфиксную.

Инфиксная – знак операций стоит между операндами (используемая нами до сих пор) x Ù(y Ú z) или x and (y or z);

Префиксная (прямая польская запись) – знак операций стоит перед операндами Ù x Ú y z;

Постфиксная (обратная польская запись) – знак операций стоит после операндов x y z Ú Ù

Постфиксная запись при считывании формулы позволяет однозначно указать порядок выполнения операций.

Преобразование инфиксной формы в префиксную и постфиксную

Рассматриваем операции согласно их очередности выполнения

знак операции выносим либо вперед операндов (префиксная форма) либо располагаем сзади операндов (постфиксная форма)

Представить инфиксную форму в префиксную и постфиксную (х3Úх1)&x1&(x1Åx2)

(х3 Ú х1) & x1 & (x1 Å x2) (х3 Ú х1) & x1 & (x1 Å x2)

Префиксная постфиксная

Ú (х3, х1) & x1 & (x1 Å x2) (х3 х1 Ú) & x1 & (x1 Å x2)

( Ú х3 х1) & x1 & (Å x1x2) (х3 х1 Ú ) & x1 & (x1x2 Å)

(& ( Ú х3 х1) x1) & (Å x1x2) ((х3 х1 Ú ) x1 &) & (x1 x2 Å )

& & Ú х3 х1 x1 Å x1 x2 х3 х1 Ú x1 & x1x2 Å &

Преобразование постфиксной формы в инфиксную

Выражение просматриваем слева направо, и его элементы помещаются в стек

Если в стеке находятся два элемента и операция (а b F), то эта тройка изымается из стека и выполняется операция

(a F b).

Результат операции помещается в стек

Просмотр строки продолжается.

Пример: представить постфиксную форму x3 x1 & x1 x1 x2Ú ÅÚ в инфиксную

x3 x1 & x1 x1 x2 Ú Å Ú

(x3& x1) x1 x1 x2 Ú Å Ú

(x3& x1) x1 (x1 Ú x2) Å Ú

(x3& x1) (x1 Å (x1 Ú x2)) Ú

(x3& x1) Ú (x1Å(x1Ú x2))

Преобразование префиксной формы в инфиксную

Выражение просматриваем слева направо, и его элементы помещаются в стек

Если возникает ситуация когда в стеке находятся знак операции и две переменные (F a b), то эта тройка изымается из стека и над ними выполняется операция

(a F b).

Результат операции помещается в стек. Просмотр продолжается.

Пример: представить префиксную форму →Úх1х2&x1x3 в инфиксную

→ Ú х1 х2 & x1 x3

→ Ú х1 х2 (x1&x3)

→ (х1 Ú х2) (x1&x3)

(х1Ú х2) → (x1&x3)

52.Элементарная конъюнкция, элементарная дизъюнкция. ДНФ, СДНФ, КНФ, СКНФ. Построение СДНФ и СКНФ по таблице истинности. Преобразования ДНФ в СДНФ. Преобразование КНФ в СКНФ.

Элементарной конъюнкцией называются элементарные переменные либо (в разделительном смысле) их отрицания соединенные конъюнкцией ùx1 & x2 & ùx3

Элементарной дизъюнкцией называются элементарные переменные либо (в разделительном смысле) их отрицания соединенные дизъюнкцией ùx1 Ú x2 Ú ùx3

Дизъюнктивно Нормальная Форма (ДНФ) – дизъюнкция элементарных конъюнкций (ùx1 & x2 & ùx3) Ú (x1 & ùx2 & x3)

 

Конъюнктивно Нормальная Форма (КНФ)– конъюнкция элементарных дизъюнкций (ùx1 Ú x2 Ú ùx3) & (x1 Ú ùx2 Ú x3)

СДНФ и СКНФ

Совершенная Дизъюнктивно Нормальная Форма (СДНФ) – это ДНФ, у которой все элементарных конъюнкций содержат КАЖДУЮ переменную ровно один раз и все элементарные конъюнкции различны

Пример: ( ù x1 & x2 & ù x3) Ú (x1 & ù x2 & ù x3)

Совершенная Конъюнктивно Нормальная Форма (СКНФ) – это КНФ у которой все элементарных дизъюнкций содержат КАЖДУЮ переменную ровно один раз и все элементарные дизъюнкции различны)

Пример: ( ù x1 Ú x2 Úù x3) & (x1 Úù x2 Ú x3)

Любую логическую функцию можно представить в виде СДНФ и СКНФ используя таблицу истинности.

Построение СДНФ и СКНФ

Построения СДНФ

Для каждого единичного набора переменных выписываем конъюнкцию всех переменных.

Над теми переменными, которые в этом наборе равны 0, ставим отрицание.

Все такие конъюнкции соединяем дизъюнкциями.

Построения СКНФ

Для каждого нулевого набора переменных выписываем дизъюнкцию всех переменных.

Над теми переменными, которые в этом наборе равны 1, ставим отрицание.

Все такие дизъюнкции соединяем конъюнкциями.

СДНФ – ( ù x&y) Ú (x & ù y)

СКНФ – (x Ú y) & ( ù x Úù y)