Операции над соответствиями. Объединение, пересечение, дополнение, инволюция (обратное) соответствия, композиция соответствий.

Прямое и обратное соответствие Галуа и его роль в проективном распознавании образов. Свойства соответствий Галуа. Замкнутое подмножество.

Всякое соответствие R Í A ´ B устанавливает соответствие Галуа между подмножествами множества A и B. Если X Í A то соответствие Галуа это множество G(X) = Ç _{a Î X}im _R a

X Í A = {Маша, Вася}. Г(Х) = im R Маша Ç im R Вася= {Пушкин}

 

im _R Маша={ Лермонтов, Пушкин }, im _R Вася= {Достоевский, Толстой, Пушкин}.

Если Y Í B вводится обратное соответствие Галуа как множество G^–1(Y)= Ç _{b Î Y} coim _R b.

Y={Пушкин, Толстой}. coim _R Пушкин={ Петя, Маша, Вася },

coim _R Толстой= {Петя, Вася}.

Г^-1(Y) = coim _R Пушкин Ç coim _R Толстой= {Петя, Вася}

Х* = Г^-1(Г(Х)) = Г^-1({Пушкин}) = coim _R Пушкин= {Петя, Маша, Вася}

Множество людей имеющие сходные интересы с множеством Х

Из X ₁Í X ₂ следует G (X ₁) Ê G (X ₂);

Из Y ₁Í Y ₂ следует G^–1(Y ₁) Ê G^–1(Y ₂);

Пусть X * = G^–1 (G (X)), Y * = G(G^–1(Y)),

тогда X Í X *, Y Í Y *

Подмножество X Í A (Y Í B) называется замкнутым, если X = X * (Y = Y *).

Соответствие Галуа устанавливает биективное соответствие между замкнутыми подмножествами множеств A и B.

8.Бинарное отношение. Способы задания. Рефлексивное, симметричное, антисимметричное, асимметричное, транзитивное отношения.

Если 2-местное соответствие задано на одном множестве RÍ М×М, то оно чаще всего называется бинарным отношением

Пример: бинарное отношение R= «отличаться не больше чем на 1», заданное на множестве М={1,2,3,4}.

 

Список: R={(1,1), (1,2), (2,1), (2,2), (2,3), (3,2), (3,3), (3,4), (4,3), (4,4)}

Матрица Графически Граф

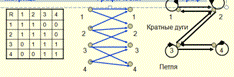
Отношение рефлексивно, если R ÊD _М, где D _М – единичная матрица размера |M|×|М|

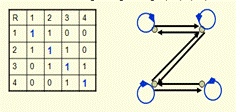
Отношение рефлексивно, если для любого элемента а∊М упорядоченная пара (а,а) ∊ R Пример: R- «жить в одном городе»

Отношение арефлексивно, если R ÇD м = Æ, где D _М – единичная матрица размера |M|×|М|

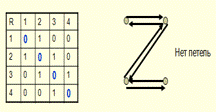
Отношение антирефлексивно, если для любого элемента а∊М упорядоченная пара (а,а) ∉ R. Пример: R- «быть начальником»

Отношение может быть не рефлексивным и не антирефлексивным

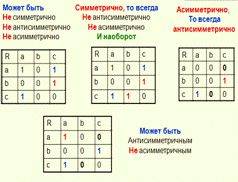
Симметричное

Если R = R^#, где R^# = {(a,b): (b,a) ÎR} обратное отношение

Для любых элементов a,b если пара (а,b)∊R, то и пара (b,a)∊R

все «1» в матрице симметричные; все дуги кратные

Антисимметричное

Если R Ç R^# Í Dм

2) Для любых элементов a и b, если (a,b) ∊ R и (b,a) ∊ R, то a=b

нет симметричных «1», на главной диагонали могут быть «1»;

нет кратных дуг, но могут быть петли

Асимметричное

Если R Ç R^# = Æ

В отношении R нет одновременно пары (a,b) и (b,a)

нет «1» на главной диагонали и симметричных;

нет ни кратных дуг ни петель

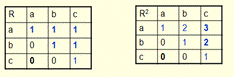
Транзитивное

Если R² Í R

(возвести матрицу в квадрат и сравнить структуры R² и R)

Если пары (а,b) ∊ R и (b,c) ∊ R, то пара (а,с) ∊ R.

Эквивалентное отношение. Классы эквивалентности. Фактормножество по отношению эквивалентности. Толерантное отношение, отношение порядка и предпорядка. Отношение строго и нестрого порядка. Отношение полного (линейного) и неполного порядка.

эквивалентное, если оно рефлексивно, симметрично и транзитивно

Пример: на множестве М={1,2,3,4,5,6} задано отношение

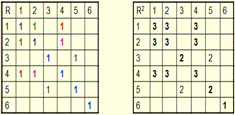
Если на множестве M задано эквивалентное отношение R, то все элементы М

можно разбить на непересекающиеся подмножества М 1 …M n

(классы эквивалентности), такие что М = М 1 È М 2 È... È М n

М 1 ∩ М 2 ∩...∩ М n = ø

Класс эквивалентности

Класс эквивалентности Mx, содержащий элемент х, состоит из элементов z∊M, таких что пара (z,x) ∊R.

Mx= {z∊M: (z,x) ∊R}

M1 = {z: (z,1) ∊R} = {1,2,4} M3 = {z: (z,3) ∊R} = {3,5}

M2 = {z: (z,2) ∊R} = {1,2,4} M5 = {z: (z,5) ∊R} = {3,5}

M4 = {z: (z,4) ∊R} = {1,2,4} M6 = {z: (z,6) ∊R} = {6}

M1=M2=M4 M3=M5

Множество классов эквивалентности F={M1, M2, …, Mn} называется фактор-множеством множества A по отношению R.

F={M1, M3, M6}

 

Число классов эквивалентности отношения эквивалентности R называют индексом множества A.

Типы Отношений

толерантное, если оно рефлексивно и симметрично;

предпорядка, если оно рефлексивно и транзитивно;

порядка, если оно транзитивно и антисимметрично;