Дадим сначала определения основных элементарных функций и элементарных функций, а затем построим графики основных элементарных функций.
Определение 1. Постоянная функция 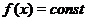 , степенная функция
, степенная функция 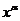 , показательная функция
, показательная функция 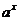 (
(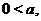
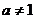 ), логарифмическая функция
), логарифмическая функция 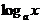
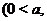
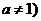 , тригонометрические функции:
, тригонометрические функции: 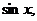
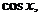
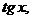
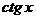 и обратные тригонометрические функции:
и обратные тригонометрические функции: 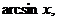
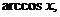
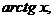
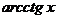 называются основными элементарными функциями.
называются основными элементарными функциями.
Определение 2. Все функции, получаемые с помощью конечного числа арифметических действий над простейшими элементарными функциями, а также конечного числа суперпозиций этих функций называются элементарными функциями.
Если график некоторой функции 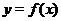 при смещении его на некоторый отрезок длины
при смещении его на некоторый отрезок длины 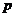 вдоль оси абсцисс совмещается сам с собой, то функция называется периодической. Длина
вдоль оси абсцисс совмещается сам с собой, то функция называется периодической. Длина 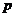 такого отрезка называется периодом функции
такого отрезка называется периодом функции  . Периодичность функции может быть кратко выражена формулой
. Периодичность функции может быть кратко выражена формулой
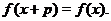
Функция  называется четной, если
называется четной, если
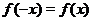
и нечетной, если
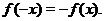
В случае когда функция не является ни четной ни нечетной, т.е. 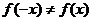 и
и 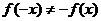 , то
, то  называется функцией общего вида.
называется функцией общего вида.
Постоянная и степенная функции
Рассмотрим постоянную функцию 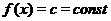 . Область ее определения - вся числовая ось
. Область ее определения - вся числовая ось  . График функции
. График функции 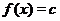 - это прямая, параллельная оси
- это прямая, параллельная оси  , проходящая через точку
, проходящая через точку 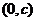 . На рис. 1 изображен график функции
. На рис. 1 изображен график функции 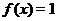 .
.
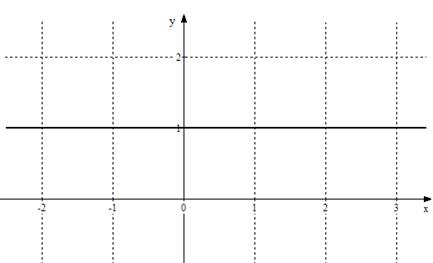
Рис. 1. График функции 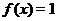 .
.
Степенная функция 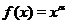 имеет график разной формы, в зависимости от значения
имеет график разной формы, в зависимости от значения 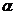 . При
. При 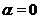 , степенная функция обращается в постоянную:
, степенная функция обращается в постоянную: 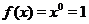 , а эта функция нами уже рассмотрена, поэтому положим
, а эта функция нами уже рассмотрена, поэтому положим 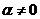 .
.
В общем случае степенная функция 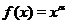 определена при
определена при 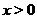 . Однако, при некоторых значениях
. Однако, при некоторых значениях 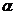 область определения функции
область определения функции 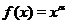 можно расширить. Рассмотрим часто встречающиеся ситуации.
можно расширить. Рассмотрим часто встречающиеся ситуации.
1. Если 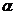 - целое положительное число:
- целое положительное число: 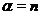 ,
, 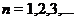 , то степенную функцию
, то степенную функцию 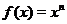 можно рассматривать на всей числовой прямой. На рис. 2 приведены графики функций
можно рассматривать на всей числовой прямой. На рис. 2 приведены графики функций 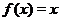 ,
, 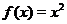 и
и 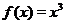 .
.
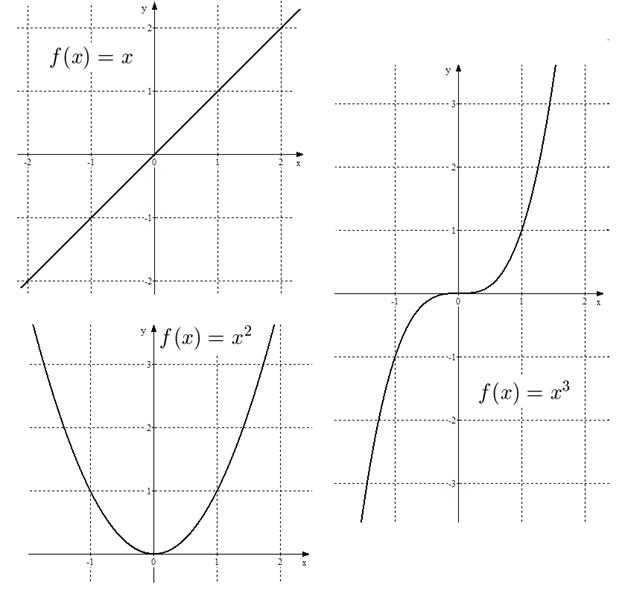
Рис. 2. Графики функций 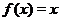 ,
, 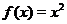 и
и 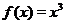 .
.
2. Если 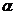 - целое отрицательное число:
- целое отрицательное число: 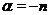 ,
, 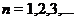 , то функция
, то функция 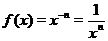 определена на всей числовой прямой за исключением точки
определена на всей числовой прямой за исключением точки 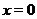 . Приведем на рис. 3 (а, б) графики функций
. Приведем на рис. 3 (а, б) графики функций 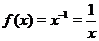 и
и 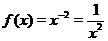 .
.
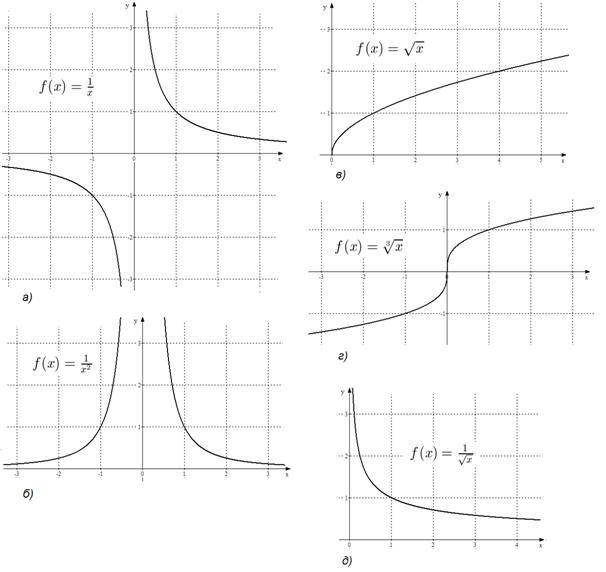
Рис. 3. Графики функций 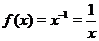 ,
, 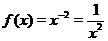 ,
, 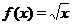 и
и 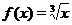 .
.
3. Если 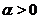 , то функция определена при
, то функция определена при 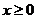 . На рис. 3 (в, г) приведены графики функций
. На рис. 3 (в, г) приведены графики функций 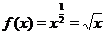 и
и 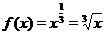 .
.
4. Если 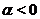 , то функция определена при
, то функция определена при 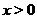 . На рис. 4 приведен график функции
. На рис. 4 приведен график функции 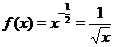 .
.
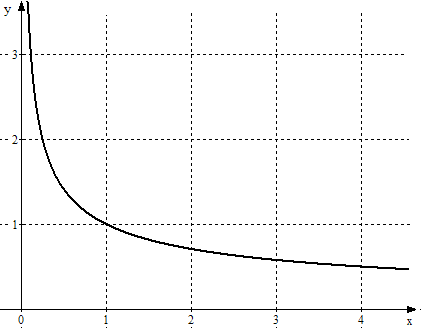
Рис. 4. График функции 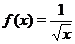 .
.
1.2. Показательная и логарифическая функции
Показательная функция 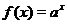 ,
, 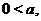
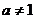 определена на всей числовой оси. Её график имеет различный вид в зависимости от значения основания (см. рис. 5). Однако, при любых значениях
определена на всей числовой оси. Её график имеет различный вид в зависимости от значения основания (см. рис. 5). Однако, при любых значениях 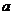 график функции
график функции 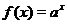 будет находиться выше оси
будет находиться выше оси 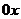 , т.к.
, т.к. 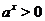 для всех
для всех  , и проходить через точку
, и проходить через точку 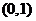 , т.к.
, т.к. 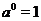 .
.
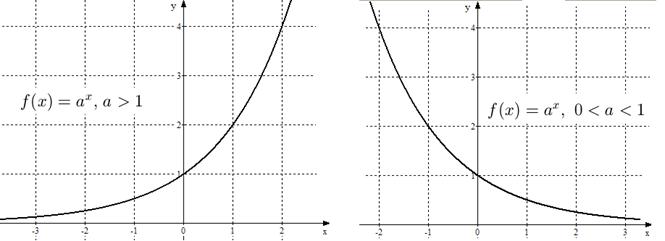
Рис. 5. Графики функции 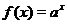 при
при 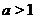 и при
и при 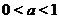 .
.
Логарифмическая функция 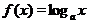 имеет смысл при
имеет смысл при 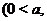
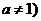 ,
, 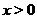 . Графики функции
. Графики функции 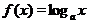 приведены на рис. 6 для
приведены на рис. 6 для 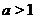 и
и 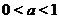 . При любом допустимом значении основания
. При любом допустимом значении основания 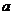 график
график 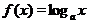 проходит через точку
проходит через точку 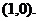
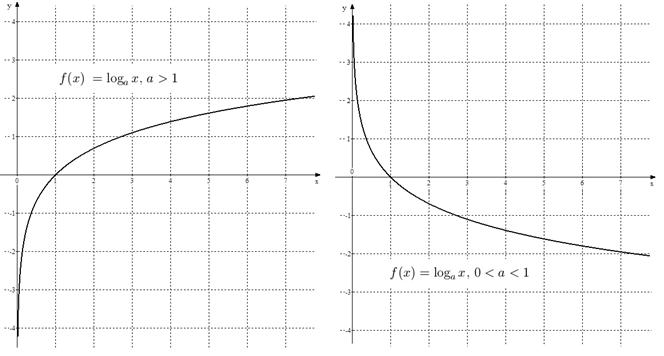
Рис. 6. Графики функции  при
при  и при
и при  .
.
Тригонометрические функции
Тригонометрические функции 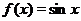 и
и 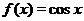 опредены на всей числовой оси, переодические, с периодом
опредены на всей числовой оси, переодические, с периодом 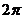 и не принимают значения по абсолютной величине большие
и не принимают значения по абсолютной величине большие 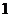 . Отметим также, что функция
. Отметим также, что функция 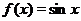 является нечетной, а функция
является нечетной, а функция 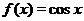 - четной. Их графики изображены на рис. 7.
- четной. Их графики изображены на рис. 7.
Линия, являющаяся графиком функции 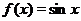 , называется синусоидой. График функции
, называется синусоидой. График функции 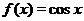 - тоже синусоида, она получается из графика
- тоже синусоида, она получается из графика 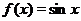 смещением вдоль
смещением вдоль 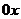 влево на отрезок
влево на отрезок 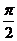 .
.
Из рис. 7 видно, что график функции 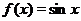 проходит через точку
проходит через точку 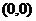 - начало координат, а функция
- начало координат, а функция 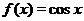 проходит через точку
проходит через точку 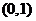 . Графики обеих функций и
. Графики обеих функций и 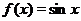 и
и 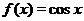 пересекают ось
пересекают ось 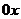 неограниченное число раз, это означает, что уравнения
неограниченное число раз, это означает, что уравнения 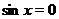 и
и 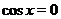 имеют бесконечно много корней. Именно, решение уравнения
имеют бесконечно много корней. Именно, решение уравнения 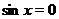 имеет вид
имеет вид 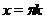 , где
, где 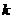 - целое число, а решением уравнения
- целое число, а решением уравнения 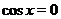 будут число
будут число 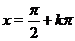 , где
, где 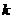 - целое число.
- целое число.
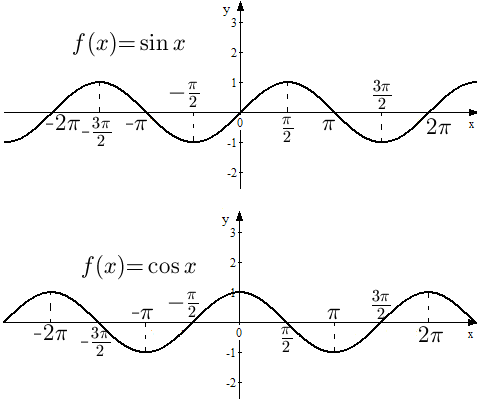
Рис. 7. Графики функции  и
и 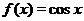 .
.
Тангенс и котангенс выражаются формулами 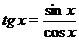 и
и 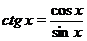 , а в такой форме записи видно, что графики этих функций будут иметь бесконечно много точек разрыва. Действительно, у
, а в такой форме записи видно, что графики этих функций будут иметь бесконечно много точек разрыва. Действительно, у  в знаменателе находится
в знаменателе находится 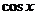 , который обращается в нуль в точках
, который обращается в нуль в точках 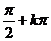 , а
, а  будет иметь разрывы там, где синус равен нулю, т.е. в точках
будет иметь разрывы там, где синус равен нулю, т.е. в точках 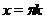 (
(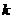 - целое число).
- целое число).
Обе функции и 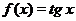 и
и 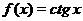 являются нечетными и периодическими с периодом
являются нечетными и периодическими с периодом 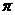 . Графики этих функций приведены на рис. 8.
. Графики этих функций приведены на рис. 8.
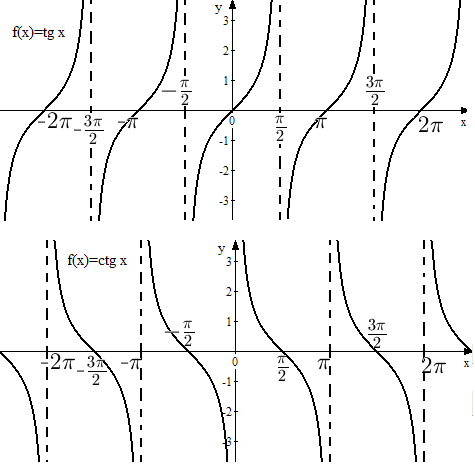
Рис. 8. Графики функции 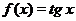 и
и 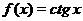 .
.



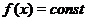 , степенная функция
, степенная функция 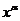 , показательная функция
, показательная функция 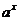 (
(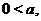
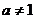 ), логарифмическая функция
), логарифмическая функция 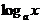
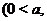
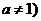 , тригонометрические функции:
, тригонометрические функции: 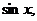
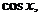
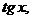
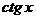 и обратные тригонометрические функции:
и обратные тригонометрические функции: 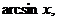
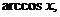
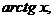
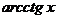 называются основными элементарными функциями.
называются основными элементарными функциями.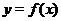 при смещении его на некоторый отрезок длины
при смещении его на некоторый отрезок длины 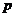 вдоль оси абсцисс совмещается сам с собой, то функция называется периодической. Длина
вдоль оси абсцисс совмещается сам с собой, то функция называется периодической. Длина  . Периодичность функции может быть кратко выражена формулой
. Периодичность функции может быть кратко выражена формулой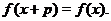
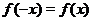
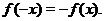
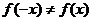 и
и 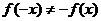 , то
, то 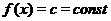 . Область ее определения - вся числовая ось
. Область ее определения - вся числовая ось 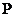 . График функции
. График функции 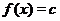 - это прямая, параллельная оси
- это прямая, параллельная оси 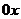 , проходящая через точку
, проходящая через точку 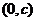 . На рис. 1 изображен график функции
. На рис. 1 изображен график функции 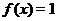 .
.
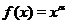 имеет график разной формы, в зависимости от значения
имеет график разной формы, в зависимости от значения 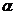 . При
. При 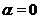 , степенная функция обращается в постоянную:
, степенная функция обращается в постоянную: 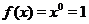 , а эта функция нами уже рассмотрена, поэтому положим
, а эта функция нами уже рассмотрена, поэтому положим 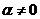 .
.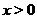 . Однако, при некоторых значениях
. Однако, при некоторых значениях 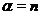 ,
, 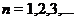 , то степенную функцию
, то степенную функцию 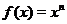 можно рассматривать на всей числовой прямой. На рис. 2 приведены графики функций
можно рассматривать на всей числовой прямой. На рис. 2 приведены графики функций 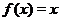 ,
, 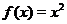 и
и 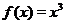 .
.
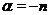 ,
, 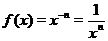 определена на всей числовой прямой за исключением точки
определена на всей числовой прямой за исключением точки 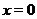 . Приведем на рис. 3 (а, б) графики функций
. Приведем на рис. 3 (а, б) графики функций 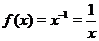 и
и 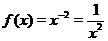 .
.
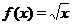 и
и 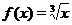 .
.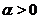 , то функция определена при
, то функция определена при 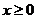 . На рис. 3 (в, г) приведены графики функций
. На рис. 3 (в, г) приведены графики функций 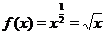 и
и 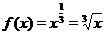 .
.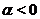 , то функция определена при
, то функция определена при 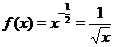 .
.
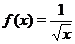 .
.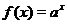 ,
, 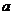 график функции
график функции 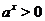 для всех
для всех  , и проходить через точку
, и проходить через точку 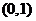 , т.к.
, т.к. 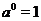 .
.
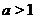 и при
и при 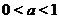 .
.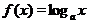 имеет смысл при
имеет смысл при 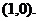

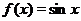 и
и 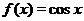 опредены на всей числовой оси, переодические, с периодом
опредены на всей числовой оси, переодические, с периодом 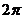 и не принимают значения по абсолютной величине большие
и не принимают значения по абсолютной величине большие 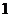 . Отметим также, что функция
. Отметим также, что функция 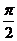 .
. - начало координат, а функция
- начало координат, а функция 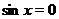 и
и 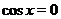 имеют бесконечно много корней. Именно, решение уравнения
имеют бесконечно много корней. Именно, решение уравнения 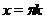 , где
, где 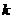 - целое число, а решением уравнения
- целое число, а решением уравнения 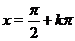 , где
, где 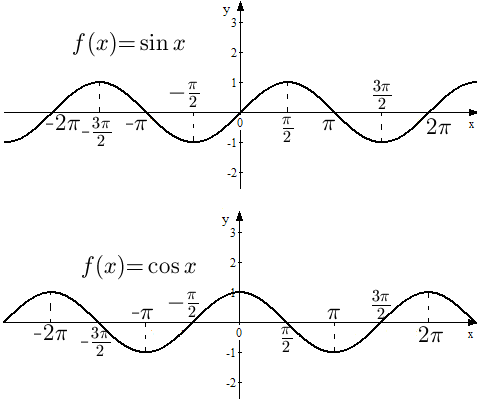
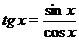 и
и 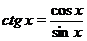 , а в такой форме записи видно, что графики этих функций будут иметь бесконечно много точек разрыва. Действительно, у
, а в такой форме записи видно, что графики этих функций будут иметь бесконечно много точек разрыва. Действительно, у 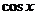 , который обращается в нуль в точках
, который обращается в нуль в точках 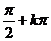 , а
, а 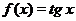 и
и 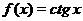 являются нечетными и периодическими с периодом
являются нечетными и периодическими с периодом 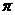 . Графики этих функций приведены на рис. 8.
. Графики этих функций приведены на рис. 8.



