

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
Топ:
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
В этом разделе мы рассмотрим как построить график функции, используя теорию пределов и дифференциальное исчисление.
1. Признак возрастания и убывания функции
Зная производную функции, мы можем выяснить на каком промежутке функция будет возрастать, а на каком убывать. Вспомним сначала определение монотонной функции.
Определение 3. Функция  , определенная на некотором промежутке вещественной оси, называется возрастающей (убывающей) на этом промежутке, если для любых
, определенная на некотором промежутке вещественной оси, называется возрастающей (убывающей) на этом промежутке, если для любых 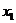 и
и 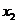 из этого промежутка, таких, что
из этого промежутка, таких, что 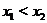 выполняется неравенство
выполняется неравенство 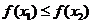 (соответственно, неравенство
(соответственно, неравенство 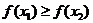 ).
).
Если функция  возрастает на некотором промежутке, то функция
возрастает на некотором промежутке, то функция  , получающаяся из
, получающаяся из  изменением знака у всех ее значений является убывающей на этом промежутке функцией.
изменением знака у всех ее значений является убывающей на этом промежутке функцией.
Возрастающие и убывающие на некотором промежутке функции называются монотонными на этом промежутке.
Если в определении 3 при 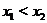 выполняется строгое неравенство
выполняется строгое неравенство 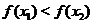 (соответственно
(соответственно 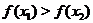 ), то функция
), то функция  называется строго возрастающей (строго убывающей).
называется строго возрастающей (строго убывающей).
Функция, строго возрастающая или строго убывающая, называется строго монотонной.
Очевидно, что строго монотонная (возрастающая, убывающая) функция является и просто монотонной (соответственно возрастающей, убывающей) функцией в смысле определения 3.
Рассмотрим некоторый интервал 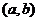 вещественной оси. Сформулируем теорему, которая содержит необходимое и достаточное условие возрастания и убывания функции на интервале
вещественной оси. Сформулируем теорему, которая содержит необходимое и достаточное условие возрастания и убывания функции на интервале 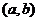 .
.
Теорема 1. Для того чтобы дифференцируемая на интервале 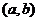 функция
функция  возрастала (убывала) на этом интервале необходимо и достаточно, чтобы во всех его точках производная этой функции была неотрицательной,
возрастала (убывала) на этом интервале необходимо и достаточно, чтобы во всех его точках производная этой функции была неотрицательной, 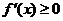 (соответственно, неположительной,
(соответственно, неположительной, 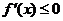 ).
).
|
|
Если всюду на 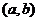 производная положительна:
производная положительна: 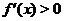 (соответственно отрицательна:
(соответственно отрицательна: 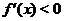 ), то функция
), то функция  строго возрастает (строго убывает) на рассматриваемом интервале.
строго возрастает (строго убывает) на рассматриваемом интервале.
Условия 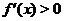 и
и 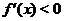 не являются необходимыми для строгого возрастания, соответственно строгого убывания, функции, Например, функция
не являются необходимыми для строгого возрастания, соответственно строгого убывания, функции, Например, функция 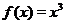 строго возрастает на любом интервале вещественной оси, но
строго возрастает на любом интервале вещественной оси, но 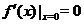 .
.
Теорема остается верной для непрерывных функций, не имеющих в конечном числе точек производной. Утверждение второй части теоремы остается в силе, если кроме того, в конечном числе точек производная обращается в нуль.
Пример 14. Найти промежутки возрастания и убывания функции  .
.
Решение. Определим производную 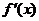 :
:
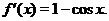
Очевидно, что 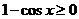 при любом значении
при любом значении  , следовательно, функция
, следовательно, функция  возрастает на всей числовой оси.
возрастает на всей числовой оси.
В частности, поскольку 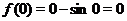 , то для всех
, то для всех 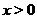 выполняется неравенство
выполняется неравенство 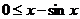 или
или

2. Локальные экстремумы функции
Введем определения локального максимума и минимума функции, а также признаки их существования.
Определение 4. Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Точка
. Точка  называется точкой локального максимума (соответственно точкой локального минимума) функции
называется точкой локального максимума (соответственно точкой локального минимума) функции  , если существует такое
, если существует такое  , что для всех
, что для всех 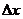 удовлетворяющих условию
удовлетворяющих условию 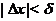 , выполняется неравенство
, выполняется неравенство 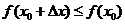 (соответственно
(соответственно 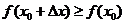 ).
).
Если существует такое  , что для всех
, что для всех 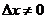 , таких, что
, таких, что 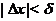 , выполняется неравенство
, выполняется неравенство 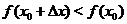 (соответственно
(соответственно 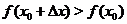 , то
, то  называется точкой строгого локального максимума (соответственно строгого локального минимума).
называется точкой строгого локального максимума (соответственно строгого локального минимума).
Точки (строгого) максимума и минимума называются точками (строгого) экстремума.
Например, на рис. 33 точки 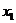 и
и 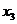 являются точками локального максимума, а точки
являются точками локального максимума, а точки 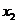 и
и 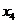 - локального минимума.
- локального минимума.
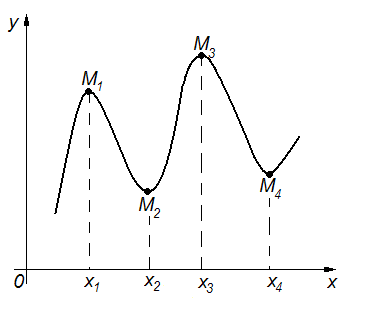
Рис. 33. Экстремумы функции.
Для точек  строгого экстремума функции
строгого экстремума функции  , и только для них, приращение
, и только для них, приращение 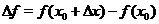 не меняет знака при переходе аргумента через
не меняет знака при переходе аргумента через  , т. е. при изменении знака
, т. е. при изменении знака 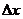 . Именно
. Именно 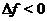 для точек строгого максимума и
для точек строгого максимума и 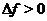 в случае строгого минимума независимо от знака достаточно малого
в случае строгого минимума независимо от знака достаточно малого 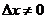 .
.
|
|
Приведем необходимые условия наличия локального экстремума функции.
Теорема 2. (необходимые условия экстремума). Пусть  является точкой экстремума функции
является точкой экстремума функции  , определенной в некоторой окрестности точки
, определенной в некоторой окрестности точки  . Тогда либо производная
. Тогда либо производная 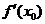 не существует, либо
не существует, либо  .
.
Отметим, что условие  не является, для дифференцируемой при
не является, для дифференцируемой при 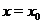 функции, достаточным условием наличия экстремума, как это показывает пример функции
функции, достаточным условием наличия экстремума, как это показывает пример функции 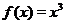 , которая для
, которая для 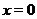 имеет производную, равную нулю, но для которой
имеет производную, равную нулю, но для которой 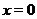 не является точкой экстремума.
не является точкой экстремума.
Приведем теперь теоремы, содержащие достаточные условия строгого локального экстремума функции в терминах смены знака производной и для функции, имеющей производные высших порядков.
Теорема 3. (достаточные условия строгого экстремума). Пусть функция  дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки  , кроме, быть может, самой точки
, кроме, быть может, самой точки  , в которой, однако, функция
, в которой, однако, функция  непрерывна. Тогда точка
непрерывна. Тогда точка  является точкой строгого максимума, если существует окрестность точки
является точкой строгого максимума, если существует окрестность точки  , в которой
, в которой 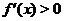 при
при 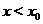 и
и 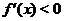 при
при 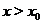 .
.
Если же 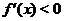 при
при 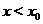 и
и 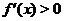 при
при 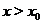 , то
, то  - точка строгого минимума.
- точка строгого минимума.
Теорема 4. Пусть в точке  у функции
у функции  существуют производные до порядка
существуют производные до порядка 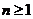 включительно, причем
включительно, причем
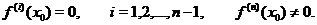
Тогда, если 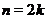 ,
, 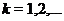 , т. е.
, т. е. 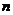 — четное число, то функция
— четное число, то функция  имеет в точке
имеет в точке  строгий экстремум, а именно максимум при
строгий экстремум, а именно максимум при 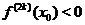 и минимум при
и минимум при 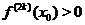 . Если же
. Если же 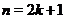 ,
, 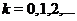 , т. е.
, т. е. 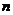 - нечетное число, то функция
- нечетное число, то функция  не имеет в точке
не имеет в точке  экстремума.
экстремума.
Следствие. Если  , а
, а 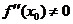 , то при
, то при 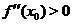
 является точкой строгого минимума, а при
является точкой строгого минимума, а при 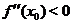 - точкой строгого максимума функции
- точкой строгого максимума функции  .
.
Отметим также, что точка, в которой функция определена, а ее производная равна нулю, называется стационарной точкой, а точка, в которой функция определена, а ее производная либо равна нулю, либо не существует, называется критической точкой.
В заключении этого пункта запишем правило нахождения тех значений  , при которых
, при которых  достигает максимума или минимума:
достигает максимума или минимума:
• нужно найти 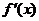 ;
;
• найти те значения  , при которых
, при которых 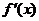 обращается в нуль или не существует, т.е. решить уравнение
обращается в нуль или не существует, т.е. решить уравнение 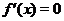 и определить точки разравы функции
и определить точки разравы функции 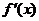 ;
;
• исследовать изменение знака 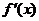 при переходе через эти значения по следующей схеме
при переходе через эти значения по следующей схеме
Таблица 5.

| 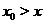
| 
| 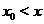
|
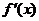
| 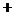
| 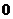
| 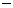
|

| 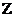
| максимум | 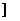
|
Таблица 6.

| 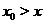
| 
| 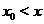
|
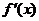
| 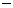
| 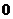
| 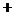
|

| 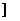
| минимум | 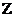
|
Значения  , в которых исследуется знак производной, нужно брать достаточно близкими к
, в которых исследуется знак производной, нужно брать достаточно близкими к  . Стрелка
. Стрелка 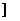 означает, что в рассатриваемом промежутке функция
означает, что в рассатриваемом промежутке функция  убывает, стрелка
убывает, стрелка 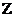 обозначает возрастание функции. Если производная сохраняет знак при переходе через
обозначает возрастание функции. Если производная сохраняет знак при переходе через  , то экстремума в точке
, то экстремума в точке  нет.
нет.
|
|
Пример 15. Найти максимумы и минимумы функции
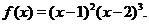
Решение. Функция определена и дифференцируема на всей числовой оси. Найдем первую производную
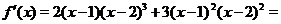
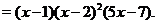
Производная определена на всей числовой оси. Очевидно, что 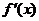 равна нулю в точках
равна нулю в точках 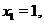
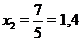 ,
, 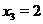 .
.
Исследуем знак 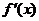 в зависимости от расположения точки
в зависимости от расположения точки  на числовой оси. Заметим, что в выражении
на числовой оси. Заметим, что в выражении 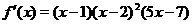 множитель
множитель 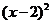 неотрицателен для всех
неотрицателен для всех  , поэтому на знак
, поэтому на знак 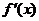 влияют только множители
влияют только множители 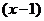 и
и 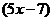 . При
. При 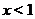 выражение
выражение 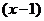 меньше нуля и
меньше нуля и 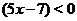 (чтобы в этом убедиться, достаточно положить
(чтобы в этом убедиться, достаточно положить  равным нулю). Когда
равным нулю). Когда 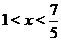 получим
получим 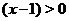 и
и 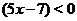 . При
. При 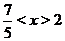 будем иметь
будем иметь 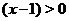 и
и 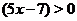 . Наконец, при
. Наконец, при 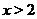 получим
получим 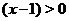 и
и 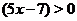 . Сведем полученные результаты в таблицу:
. Сведем полученные результаты в таблицу:
Таблица 7.

| 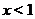
| 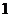
| 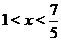
| 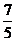
| 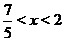
| 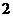
| 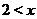
|
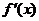
| 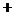
| 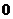
| 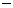
| 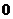
| 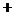
| 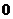
| 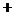
|

| 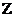
| 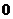 макс. макс.
| 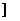
| 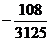 мин. мин.
| 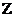
| 
| 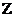
|
Итак, 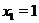 являетя точком максимума и значения функции
являетя точком максимума и значения функции  в этой точке равно
в этой точке равно 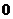 . Точка
. Точка 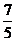 - точка минимума, при этом
- точка минимума, при этом 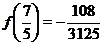 .
.
График функции 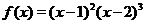 изображен на рис. 34.
изображен на рис. 34.
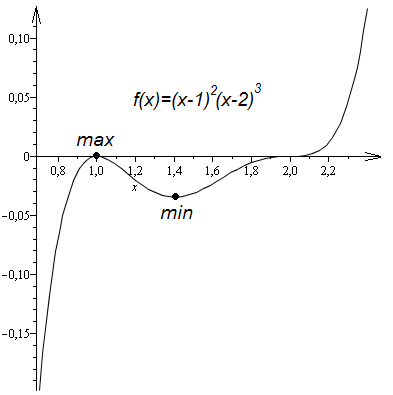
Рис. 34. График функции 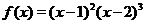 при
при 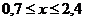 .
.
3. Выпуклость функции. Точки перегиба
В этом пункте приведем определения выпуклой вниз и выпуклой вверх функции, точек перегиба, а также сформулируем необходимые и достаточные условия выпуклости и наличия точек перегиба.
Пусть функция  определена на интервале
определена на интервале 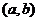 и пусть
и пусть 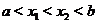 . Проведем прямую через точки
. Проведем прямую через точки 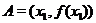 и
и 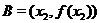 , лежащие на графике функции
, лежащие на графике функции  . Ее уравнение будет
. Ее уравнение будет
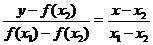
или
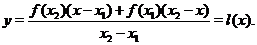
Очевидно, 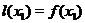 ,
, 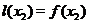 .
.
Определение 5. Функция  называется выпуклой вверх (выпуклой вниз) на интервале
называется выпуклой вверх (выпуклой вниз) на интервале 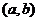 , если каковы бы ни были точки
, если каковы бы ни были точки 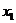 и
и 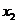 ,
, 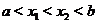 , для любой точки
, для любой точки  интервала
интервала 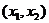 , выполняется неравенство
, выполняется неравенство 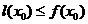 (соответственно
(соответственно 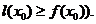
Геометрически это означает, что любая точка хорды 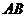 (т. е. отрезка прямой
(т. е. отрезка прямой 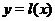 с концами в точках
с концами в точках 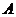 и
и 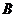 ) лежит не выше (не ниже) точки графика функции
) лежит не выше (не ниже) точки графика функции  , соответствующей тому же значению аргумента (рис. 35).
, соответствующей тому же значению аргумента (рис. 35).
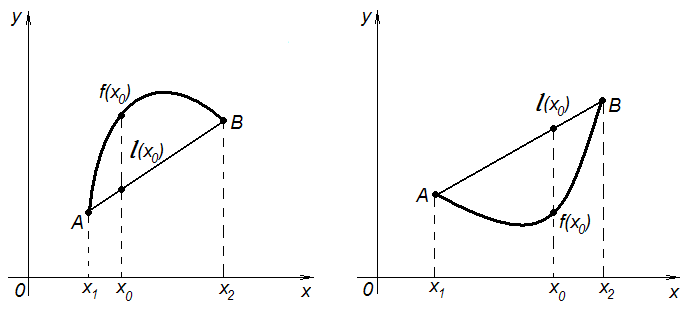
Рис. 35. Выпуклость вверх и выпуклость вниз
Определение 6. Если вместо  (соответственно,
(соответственно,  выполняются строгие неравенства
выполняются строгие неравенства  (соответственно,
(соответственно, 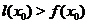 ) при любых
) при любых  ,
, 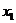 и
и 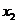 таких, что
таких, что 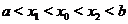 , то функция
, то функция  называется строго выпуклой вверх (строго выпуклой вниз) на интервале
называется строго выпуклой вверх (строго выпуклой вниз) на интервале 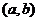 .
.
Сформулируем теорему, содержащую необходимые и достаточные условия выпуклости функции вверх и вниз.
|
|
Теорема 5. Пусть функция  определена и непрерывна вместе со своей производной
определена и непрерывна вместе со своей производной 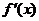 на интервале
на интервале 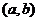 и имеет внутри него конечную вторую производную
и имеет внутри него конечную вторую производную 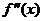 . Для выпуклости вверх (вниз) функции
. Для выпуклости вверх (вниз) функции  на интервале
на интервале 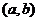 необходимо и достаточно, чтобы внутри
необходимо и достаточно, чтобы внутри 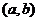 было
было 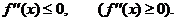
Замечание. Условие 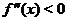 (
(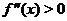 ),
), 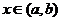 является достаточным условием строгой выпуклости вверх (вниз) функции
является достаточным условием строгой выпуклости вверх (вниз) функции  на интервале
на интервале 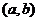 .
.
Определим теперь какая точка является точкой перегиба функции.
Определение 7. Пусть функция  дифференцируема при
дифференцируема при 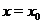 и пусть
и пусть 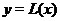 - уравнение касательной к графику функции
- уравнение касательной к графику функции  в точке
в точке 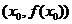 . Если разность
. Если разность 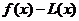 меняет знак при переходе через точку
меняет знак при переходе через точку  , то
, то  называется точкой перегиба функции
называется точкой перегиба функции  (см. рис. 36).
(см. рис. 36).
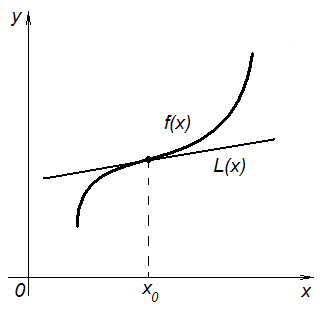
Рис. 36. Точка перегиба
Сформулируем необходимые условия существования точки перегиба.
Теорема 6. (необходимое условие наличия точки перегиба) Пусть функция  имеет непрерывную при
имеет непрерывную при 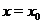 вторую производную. Тогда, если точка
вторую производную. Тогда, если точка  является точкой перегиба функции
является точкой перегиба функции  , то
, то 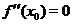 .
.
Приведем теперь достаточные условия существования точек перегиба с использованием второй и третьей производной функции.
Теорема 7. (первое достаточное условие наличия точек перегиба) Если функция  , дифференцируемая в точке
, дифференцируемая в точке  , дважды дифференцируема в некоторой проколотой окрестности
, дважды дифференцируема в некоторой проколотой окрестности 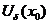 этой точки и вторая производная
этой точки и вторая производная 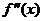 функции
функции  меняет знак при переходе аргумента через
меняет знак при переходе аргумента через  (т. е. либо
(т. е. либо 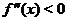 при
при 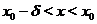 и
и 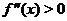 при
при 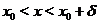 , либо
, либо 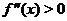 при
при 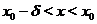 и
и 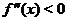 при
при 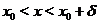 ), то
), то  является точкой перегиба функции
является точкой перегиба функции  .
.
Если исследуемая функция имеет третью производную, то можно использовать следующий признак существования точек перегиба.
Теорема 8. (второе достаточное условие наличия точек перегиба) Пусть 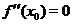 ,
, 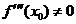 ; тогда
; тогда  является точкой перегиба.
является точкой перегиба.
Таким образом, нахождения точек перегиба и промежутков выпуклости вверх и выпуклости вниз функции  проводится следующим образом:
проводится следующим образом:
• определяется 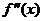 ;
;
• отыскиваются те значения  , при которых
, при которых 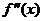 обращается в нуль или не существует, т.е. решается уравнение
обращается в нуль или не существует, т.е. решается уравнение 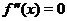 и определяются точки разрывы функции
и определяются точки разрывы функции 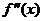 ;
;
• исследуется изменение знака 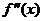 при переходе через эти значения по следующей схеме
при переходе через эти значения по следующей схеме
Таблица 8.

| 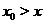
| 
| 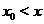
|
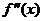
| 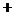
| 
| 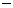
|

| 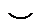
| точка перегиба | 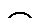
|
Таблица 9.

| 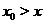
| 
| 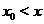
|
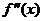
| 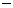
| 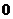
| 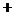
|

| 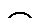
| точка перегиба | 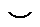
|
Значения  , в которых исследуется знак второй производной, нужно брать достаточно близкими к
, в которых исследуется знак второй производной, нужно брать достаточно близкими к  . Символ
. Символ  означает, что в рассатриваемом промежутке функция
означает, что в рассатриваемом промежутке функция  выпукла вверх, символ
выпукла вверх, символ 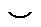 означает выпуклость вниз функции. Если вторая производная сохраняет знак при переходе через
означает выпуклость вниз функции. Если вторая производная сохраняет знак при переходе через  , то
, то  не является точкой перегиба.
не является точкой перегиба.
Пример 16. Найти интервалы выпуклости и точки перегиба функции 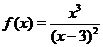 .
.
Решение. Функция определена и по крайней мере дважды дифференцируема при всех вещественных  кроме
кроме 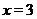 . Найдем
. Найдем 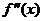 :
:
|
|
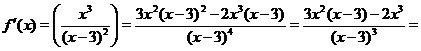
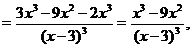
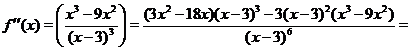
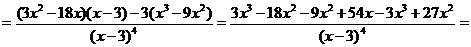
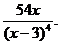
Получаем, что вторая производная 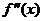 равна нулю в точке
равна нулю в точке 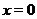 , а в точке
, а в точке 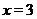 не существует. Исследует знак
не существует. Исследует знак 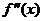 на интервалах
на интервалах 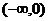 ,
, 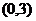 ,
, 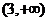 , для этого заполним следующую таблицу.
, для этого заполним следующую таблицу.
Таблица 10.

| 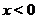
| 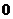
| 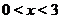
| 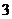
| 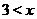
|
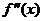
| 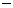
| 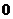
| 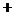
| не сущ. | 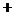
|

| 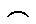
| 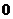 точка перегиба точка перегиба
| 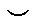
| не сущ. | 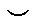
|
Получаем, что 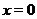 - точка перегиба, при
- точка перегиба, при 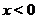 функция
функция  выпукла вверх, а при
выпукла вверх, а при 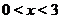 и
и 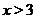 - выпукла вниз.
- выпукла вниз.
График функции 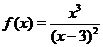 изображен на рис. 37.
изображен на рис. 37.
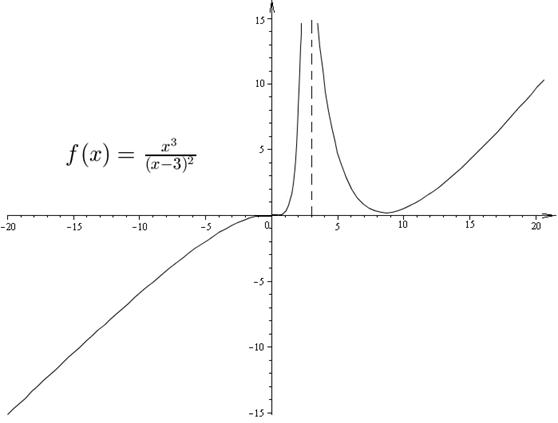
Рис. 37. График функции 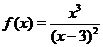 .
.
4. Асимптоты
Использование понятия предела часто позволяет более точно отразить свойства функции при построении ее графика. Так нахождение наклонной и вертикальной асимптот основывается на вычислении предела.
Асимптота может быть определена как прямая, расстояние до которой от графика функции стремится к нулю, когда точка 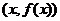 «стремится, оставаясь на графике, в бесконечность» (при
«стремится, оставаясь на графике, в бесконечность» (при 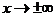 ). (см. рис. 38).
). (см. рис. 38).
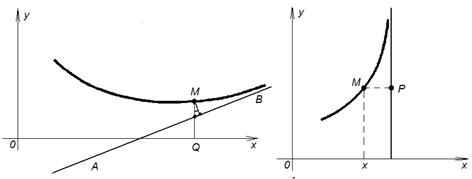
Рис. 38. Наклонная и вертикальная асимптоты.
Дадим точное определение наклонной асимптоты.
Определение 8. Пусть функция  определена для всех
определена для всех 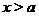 (соответственно для всех
(соответственно для всех 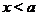 ). Если существуют такие числа
). Если существуют такие числа 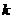 и
и 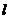 , что
, что
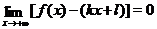
(соответственно при 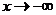 ), то прямая
), то прямая
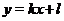
называется наклонной асимптотой графика функции  при
при 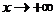 (соответственно при
(соответственно при 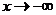 ).
).
Числа 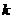 и
и 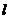 находятся по формулам
находятся по формулам
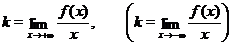
и
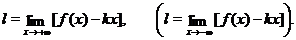
Заметим, что при таком определении мы ни при каких значениях 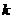 и
и 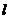 не можем получить прямую, параллельную оси
не можем получить прямую, параллельную оси 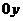 , поэтому приведем еще одно определение - определение вертикальной асимптоты.
, поэтому приведем еще одно определение - определение вертикальной асимптоты.
Определение 9. Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  (быть может, односторонней) и пусть выполнено хотя бы одно из условий
(быть может, односторонней) и пусть выполнено хотя бы одно из условий 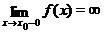 , или
, или 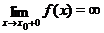 , тогда прямая
, тогда прямая 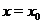 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  .
.
5. Порядок построения графика функции, заданной выражением 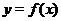
Приведем схему действий, которые нужно проделать для построения графика функции 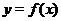 .
.
Нужно
• найти область определения функции и исследовать поведение функции в граничных точках области определения;
• исследовать функцию на симметрию графика и периодичность;
• найти точки разрыва функции и промежутки непрерывности;
• определить точки пересечения графика функции с координатными осями и области постоянства знака функции;
• найти асимптоты;
• найти точки экстремума и промежутки возрастания и убывания функции;
• определить точки перегиба и установить промежутки вогнутости вверх (вниз);
• построить график функции.
Пример 17. Построить график функции 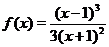 .
.
Решение. Проведем полное исследование функции.
1. Найдем область определения этой функции. Функция существует при всех значениях 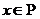 , кроме
, кроме 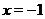 , при котором знаменатель обращается в нуль. Следовательно, область определения функции
, при котором знаменатель обращается в нуль. Следовательно, область определения функции
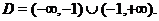
2. Исследуем вопрос о симметрии графика, т.е. проверим является ли данная функция четной, нечетной или функцией общего вида. Для этого выясним, выполняется ли одно из равенств 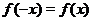 или
или 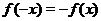 :
:
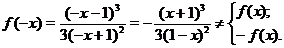
Ни одно из проверяемых равенств не выполняется, так что функция не является ни четной ни нечетной.
Очевидно, функция не является переоидической.
3. Числитель и знаменатель дроби 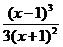 непрерывные функции, поэтому функция
непрерывные функции, поэтому функция 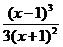 будет непрерывной при всех значениях
будет непрерывной при всех значениях  , кроме
, кроме 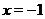 , при котором знаменатель дроби обращается в нуль.
, при котором знаменатель дроби обращается в нуль.
4. Определим точки пересечения графика функции с осями координат. График пересекает ось 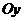 при
при 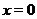 :
:
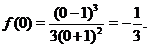
Для нахождения точек пересечения графика с осью 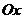 решим уравнение
решим уравнение
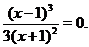
Оно имеет единственное решение: 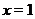 . Таким образом, точки пересечения с координатными осями:
. Таким образом, точки пересечения с координатными осями: 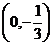 и
и 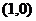 .
.
Найдем области постоянства знака функции, т.е. промежутки где функция положительна и отрицательна. Поскольку график пересекает ось 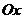 в точке
в точке 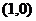 , а также поскольку функция может принимать значения разных знаков по разные стороны от точки разрава, то нужно исследовать какой знак имеет функция при
, а также поскольку функция может принимать значения разных знаков по разные стороны от точки разрава, то нужно исследовать какой знак имеет функция при 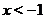 ,
, 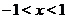 и при
и при 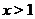 . О<
. О<
|
|
|

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!