Построение графика функции на основе её полного анализа.

1) Нахождение области определения функции.

2) Исследование поведения функции на границе области определения, нахождение вертикальных асимптот.

3) Исследование функции на четность или нечетность.(Функция является четной, если . Четность функции указывает на симметрию графика относительно оси ординат. Функция является нечетной, если . Нечетность функции указывает на симметрию графика относительно начала координат.)

4) Нахождение промежутков возрастания и убывания функции, точек экстремума. (Промежутки возрастания и убывания являются решениями неравенств и соответственно.) Чтобы определить промежутки возрастания и убывания функции:

· во-первых, находим производную;

· во-вторых, находим критические точки;

· в-третьих, разбиваем область определения критическими точками на интервалы;

· в-четвертых, определяем знак производной на каждом из промежутков. Знак «плюс» будет соответствовать промежутку возрастания, знак «минус» - промежутку убывания.

5) Нахождение промежутков выпуклости и вогнутости функции и точек перегиба. (Промежутки вогнутости и выпуклости функции находятся при решениями неравенств 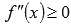и 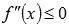соответственно.) чтобы определить промежутки вогнутости и выпуклости функции:

· во-первых, находим вторую производную;

· во-вторых, находим нули числителя и знаменателя второй производной;

· в-третьих, разбиваем область определения полученными точками на интервалы;

· в-четвертых, определяем знак второй производной на каждом из промежутков. Знак «плюс» будет соответствовать промежутку вогнутости, знак «минус» - промежутку выпуклости.

6) Нахождение горизонтальных и наклонных асимптот.

7) Построение графика.

 

Первообразная функция. Неопределенный интеграл и его основные свойства

 

Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x).

Обозначение

где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.
Свойства неопределенного интеграла

1) Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

2) Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

3) Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

4) Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

Таблица неопределенных интегралов от основных элементарных функций.

 

 

Основные методы интегрирования

 

Замена переменной

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводащимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно oпpeделить подстановку пpиобpетaeтcя практикой.

Пусть тpебyетcя вычислить интеграл Сделаем подстановку

х =φ(t), где φ(t) - функция, имеющая непрерывную производную.

Тогда dx=φ^'(t) dt и на основании свойства инвариантности формулы интегрирования неопpeделeннoгo интеграла получаем формулу интегриpoвaния подcтaнoвкoй

(30.1)

Формула (30.1) также называется формулой замены переменных в неопределeннoм интеграле. Пoслe нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования t назад к переменной х.

Иногда целесообразно подбирать подстановку в виде t= φ(х), тогда

Другими слoвaми, формулу (30.1) можно применять справа налево.