Действительные числа образуют совокупность элементов, обладающую следующими свойствами.
Если a и b - действительные числа (алгебраические, рациональные, целые, положительные целые), то таковыми же являются и
a + b и ab (замкнутость), (1)
a + b = b + a, ab = ba (коммутативность), (2)
a + (b + c) = (a + b) + c = a + b + c, a (bc) = (ab) c = abc (ассоциативность), (3)
a * 1 = a (единица), (4)
a (b + c) = ab + ac (дистрибутивность), (5)
;из a + c = b + c следует a = b, из ca = cb, 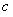
 , следует a = b (сокращение). (6)
, следует a = b (сокращение). (6)
Действительное число 0 (нуль) обладает свойствами a + 0 = a, a * 0 = 0 для каждого действительного числа a.
(Единственное) противоположное число - a и (единственное) обратное число a -1 = 1/ a для действительного числа a определяются соответственно так:
a + (- a) = a - a = 0, aa -1 = 1 (
 ).
).
Помимо "алгебраических" свойств, класс положительных целых, или натуральных, чисел 1, 2,... обладает свойством упорядоченности (n > m, если n = m + x, где x - некоторое натуральное число) и полной упорядоченности (каждое непустое множество натуральных чисел имеет наименьший элемент). Множество натуральных чисел, содержащее число 1 и для каждого из своих элементов n следующий за ним элемент n + 1, содержит все натуральные числа (принцип полной индукции).
Свойства натуральных чисел могут быть выведены из пяти аксиом Пеано: 1) 1 есть натуральное число; 2) для каждого натурального числа N существует единственное следующее за ним натуральное число S (n); 3) 
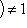 ; 4) из S (n) = S (m) следует n = m и 5) имеет место принцип полной индукции. (При его формулировке элемент, следующий за n, обозначается через S (n).) Сложение и умножение, подчиняющиеся правилам (1)-(6), определяются "рекуррентными" соотношениями
; 4) из S (n) = S (m) следует n = m и 5) имеет место принцип полной индукции. (При его формулировке элемент, следующий за n, обозначается через S (n).) Сложение и умножение, подчиняющиеся правилам (1)-(6), определяются "рекуррентными" соотношениями
n + 1 = S (n),
n + S (m) = S (n + m),
n *1 = n,
n * S (m) = n * m + n.
Целыми числами называются числа вида n, - n и 0, где n - натуральное число, а рациональными - числа вида p / q, где p и q - целые числа и 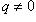 .
.
Действительные числа можно ввести, исходя из множества рациональных чисел, с помощью предельного процесса. Действительные числа, не являющиеся рациональными, называются иррациональными.
Отношение равенства. Из a = b следует b = a (симметрия отношения равенства), a + c = b + c и ac = bc (вообще f(a) = f(b), если f(a) обозначает некоторую операцию, приводящую к единственному результату). Из a = b и b = c следует a = c (транзитивность отношения равенства). Из следует и.
Отношение тождества. Вообще говоря, уравнение относительно какой-либо величины x или нескольких величин x1, x2,... будет удовлетворяться только при некоторых специальных значениях x или специальных множествах значений x1, x2,... Если хотят подчеркнуть тот факт, что какое-нибудь уравнение удовлетворяется при всех значениях x или x1, x2,... в известных представляющих интерес пределах, то вместо символа = иногда пользуются символом тождества (пример: (x - 1)(x + 1) x2 - 1), а пределы изменения рассматриваемых переменных иногда указывают справа от уравнения. Символ a b употребляется также в смысле: "a по определению равно b".
Неравенства. Действительное число a может быть положительно (a > 0), отрицательно (a < 0) или равно нулю (a = 0). Сумма и произведение положительных чисел положительны.





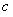
 , следует a = b (сокращение). (6)
, следует a = b (сокращение). (6)
 ).
).
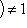 ; 4) из S (n) = S (m) следует n = m и 5) имеет место принцип полной индукции. (При его формулировке элемент, следующий за n, обозначается через S (n).) Сложение и умножение, подчиняющиеся правилам (1)-(6), определяются "рекуррентными" соотношениями
; 4) из S (n) = S (m) следует n = m и 5) имеет место принцип полной индукции. (При его формулировке элемент, следующий за n, обозначается через S (n).) Сложение и умножение, подчиняющиеся правилам (1)-(6), определяются "рекуррентными" соотношениями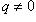 .
.


