Рефлексивные, симметричные, транзитивные отношения

 

1. Обратимся теперь к некоторым типам отношений, обладающих свойствами, которые представляют особый интерес.

Рефлексивное отношение – бинарное отношение, обладающее свойством: для любого а выполнено аRa.

Aнтирефлексивное отношение – бинарное отношение, обладающее свойством: для любого а выполнено а 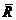a.

Cимметричное отношение – бинарное отношение, обладающее свойством: для любых a, b выполнено aRb Þ bRa (т.е. из aRb следует bRa).

Антисимметричное отношение – такое бинарное отношение, что для любых выполнено: если a ≠ b, то aRb Þ b 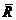a (т.е. если a и b – в этом порядке(!) – находятся в отношении R, то b и a – нет). Это же свойство выражают иначе: если aRb и bRa, то a = b.

Примеры: 1) отношения равенства рефлексивны и симметричны;

2) отношения между парами чисел «больше», «меньше» – антирефлексивны и антисимметричны;

3) отношение параллельности прямых рефлексивно и симметрично;

4) отношение перпендикулярности прямых антирефлексивно и симметрично;

5) отношение инцидентности точки и прямой симметрично.

Понятие симметрии можно распространить и на отношения большей арности, имея в виду симметрию для отдельных пар в n -наборе. Так, тернарное отношение R (X, Y, Z) симметрично по паре Y, Z, если R (a, b, c) всегда выполняется вместе с R (a, c, b). Например, отношение (X – Y = Z) симметрично по (Y, Z). Действительно, если X – Y = Z, то X – Z = Y,
т.е. перестановка Y и Z не изменяет равенства.

2. Транзитивное отношение – бинарное отношение, обладающее свойством: для любых
трех элементов a, b, c выполнено: если aRb и bRc, то aRc (если в отношении R находятся a и b, а также b и c, тов этом отношении находятся а и c).

Примеры транзитивности:

1) отношения «больше» и «меньше» (если а > b и b > c, то a > c);

2) отношение параллельности прямых (для прямых l ₁, l ₂, l ₃, если l ₁ 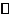l ₂ и l ₂ 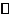l ₃, то l ₁ 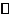l ₃);

3) отношения равенства чисел;

4) отношения «правее», «левее» между делениями на линейной шкале прибора;

5) отношения «севернее», «южнее» между точками земной поверхности;

6) отношение «быть прямым начальником».

Примеры нетранзитивных отношений:

1) отношение перпендикулярности прямых (для прямых l ₁, l ₂, l ₃, если l ₁ 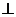l ₂и l ₂ 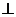l ₃, то l ₁не перпендикулярна l ₃);

2) известное из истории европейского средневековья отношение между вассалом и сюзере-ном, выражавшееся формулой: «вассал моего вассала – не мой вассал»;

3) отношение между игроками или командами в спортивном турнире: «участник Х выиграл у участника Y»: возможно, что А выиграл у В, В выиграл у С, но А проиграл С;

4) отношения «западнее», «восточнее» между точками земной поверхности: Ярославль
(40° восточной долготы) западнее Хабаровска (135° восточной долготы); Хабаровск западнее Торонто (80° западной долготы), но Ярославль восточнее Торонто;

5) отношение «быть непосредственным начальником».

Упражнение. Тернарное отношение примера 5 (в конце п. 4.1) «точки А и В на плоскости находятся по разные стороны от прямой l» превращается в бинарное отношение между
двумя точками, если зафиксировать прямую l. Является ли это бинарное отношение транзитивным?

В табл. 4.1 сведены характеристики рассмотренных выше четырех отношений R ₁, R ₂, R ₃, R ₄ (пример в п. 4.1).

Таблица 4.1

 

Для рефлексивного (соответственно, антирефлексивного) отношения все диагональные элементы матрицы равны 1 (соответственно, 0). Матрица симметричного отношения симметрична относительно главной диагонали, т.е. для всех i, j выполнено равенство а_ij = a_ji. Для антисимметричного отношения соответственно выполнено а_ij ≠ a_ji).

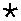Транзитивное замыкание a 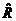b бинарного отношения R есть бинарное отношение 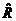такое, что элементы a и b находятся в отношении 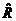, если существует цепочка c ₁, c ₂,..., c_k, для которой выполнено aRc ₁, c ₁ Rc ₂,..., c_kRb. Например, для отношения «быть сыном» транзитивным замыканием является отношение «быть прямым потомком по мужской линии». Для отношения на множестве квартир дома «иметь общую стену» транзитивное замыкание – это отношение «находиться на одном этаже». Отношение 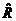, конечно, транзитивно.

Упражнения. 1. Сравните отношения выражаемые служебными терминами «непосредствен-ный начальник» и «прямой начальник»; например, командир отделения, командир взвода, командир роты и т.д. по отношению к рядовому.

2. Является ли транзитивным бинарное отношение П(X, Y) между реками: «река Х является притоком реки Y»? Сформулируйте, каким географическим термином выражается отношение (X, Y), представляющее транзитивное замыкание бинарного отношения П(X, Y).

 

 

Отношения эквивалентности

 

Отношение эквивалентности – бинарное отношение, обладающее свойствами рефлексивности, симметричности и транзитивности.

Примеры.

1. Рассмотренные выше отношения равенства для геометрических фигур или чисел.

2. Отношение параллельности прямых или плоскостей.

3. Отношение подобия треугольников.

4. Отношение пропорциональности Р между парами чисел (X, Y) и (Z, T): (X, Y) P (Z, T), если X/Y = Z/T.

5. Отношение «быть одноклассниками» между учащимися школы;

6. Упоминавшееся выше отношение между целыми числами – «иметь одинаковые остатки от деления на 7».

Пусть на множестве М введено некоторое отношение эквивалентности R. Для каждого элемента α Î M рассмотрим множество M_α = { β: αRβ } элементов M, эквивалентных α. В силу симметричности и транзитивности отношения R, если αRβ, то M_α = M_β. Если же α 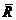β,
то M_α ∩ M_β = Æ; иначе, если бы существовал элемент γ Î M_α ∩ M_β, то выполнялось бы αR γ
и βR γ, в силу транзитивности R, αRβ.

Таким образом, система различных множеств { M_α } – разбиение множества M (полнота разбиения обусловлена рефлексивностью R), и тем самым, каждое отношение эквивалентности R на множестве порождает разбиение этого множества на классы эквивалентности бинарного отношения R на множестве – систему подмножеств множества такую, что:

1) любые два элемента из одного класса эквивалентны;

2) любые два элемента из разных классов не эквивалентны.

Верно и обратное. Любое разбиение множества M можно рассматривать как отношение эквивалентности, в котором находятся пары элементов, отнесенные к одному и тому же классу разбиения, и не находятся элементы из разных классов.

Группировку объектов, применяемую в статистике, законодательстве и в других областях (например, разделение предприятий на малые, средние и крупные для установления нормативов, единых для всех элементов группы), можно рассматривать как установление эквивалентности.

Классы эквивалентности для примеров 2–6:

(2) – множества параллельных друг другу прямых или плоскостей; если прямые (плоскости) пересекаются – они в разных классах;

(3) – множества подобных друг другу треугольников; в разных классах – треугольники разной формы;

(4) – пары чисел (X, Y), имеющих одинаковое значение частного X / Y;

(5) – учащиеся одного школьного класса;

(6) – семь классов чисел N_k (k = 0, 1,..., 6), имеющих остаток k при делении на 7;

Класс N_k содержит числа вида 7 n + k (n = 0, ±1, ±2,...). Например, для k = 4 класс N ₄ – это множество (..., -10, -3, 4, 11, 18, 25,...).

Рассмотрим еще один важный пример. Определим отношение Э между множествами следующим образом: Э (L, M), или короче LЭM –, если существует взаимно однозначное соответствие между множествами L и M. Можно показать, что Э является отношением эквивалентности. Действительно, если для трех множеств L, M, K выполнено LЭM и MЭK, то элементу l Î L соответствует некоторый элемент m Î M, а элементу m Î M соответствует элемент k Î K, и оба этих взаимно однозначных соответствия – симметричные отношения; тогда LЭK, поскольку можно сопоставить элементу l элемент k, и это соответствие также взаимно однозначно. Классы эквивалентности состоят при этом из множеств, имеющих одинаковую мощность (для конечных множеств – одинаковое число элементов).

 

 

Отношения порядка

 

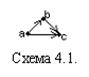1. Отношения порядка x í y (читается: x предшествует y)обладают двумя свойствами:

1) если (a í b) и (b í c), то (a í c), т.е. x í y – транзитивное отношение
(схема 4.1);

2) если (a í b) и a ¹ b, то не выполнено (b í a), т.е. x í y – антисимметричное отношение.

Первое условие означает, что если первый из трех элементов предшествует второму, а второй предшествует третьему, то первый предшествует третьему. Второе условие означает, что два различных элемента не могут предшествовать друг другу.

Отношение порядка x í y может быть строгим, если оно антирефлексивно, и нестрогим, если оно рефлексивно. Примерами строгого порядка могут служить отношения "больше", "меньше", "старше" и т.п. Для чисел обычное обозначение порядка – знаки "<, >". Для нестрогого порядка, наряду с естественными примерами (a £ b, a ³ b) неравенств для чисел, примером может служить отношение между точками плоскости или пространства "находиться ближе к началу координат".

Если в спортивном соревновании не предусматривается дележ мест (т.е. каждый участник получает определенное, только ему присужденное место), то это пример строгого порядка; в противном случае – нестрогого.

Отношения порядка устанавливаются на множестве различными способами. Установление для множества некоторого отношения порядка называется его упорядочением, а само множество в результате этого становится упорядоченным. Для конечного множества любая перестановка его элементов задает некоторый строгий порядок. Бесконечное множество можно упорядочить бесконечным множеством способов.

Элементы множества можно в одних случаях рассматривать как упорядоченные, а в других как неупорядоченные. Так, команда из 4 спортсменов – участников эстафеты – упорядоченная четверка (важно распределение по этапам); а 4 участника кросса – неупорядоченное множество. Отношение порядка на множестве М устанавливает на нем иерархию.

2. Если для отношения порядка í на множестве М и некоторых различных элементов a, b Î M выполняется хотя бы одно из отношений a í b или b í a, то элементы а и b называются сравнимыми; в противном случае – несравнимыми.

Пример. Несколько лет назад одно из правил пользования московским метрополитеном не разрешало провоз громоздких предметов, если их размеры по длине, ширине и высоте больше 80´60´40 см. Из этой формулировки не ясно, как сравнивать векторы – тройки размеров: запрещено или нет превышение хотя бы по одному из трех размеров (например, допустимы ли размеры 90´35´30 или 50´45´45 и т.п.). В современных правилах – точная формулировка: сумма трех измерений не должна превышать 150 см. Это уже означает, что сопоставляются числа, а все числа сравнимы.

Линейно упорядоченное множество М – множество, на котором задано отношение порядка, причем любые два элемента множества М сравнимы; частично упорядоченное множество –
то же, но допускаются несравнимые пары элементов.

Линейно упорядоченным является множество точек на прямой с отношением “правее”, множества целых, рациональных, действительных чисел с отношением “больше” и т.п.

Примером частично упорядоченного множества могут служить соотношения между основными (I–IV) группами крови у человека: они определяются наличием или отсутствием
двух антигенов A и B (например, группа II, т.е. тип A 0 означает наличие A и отсутствие B). Частичный порядок X í Y (нестрогий), представлен на рис. 4.2; он обозначает возможность переливания крови типа X обладателю крови типа Y. Группа I (тип 00) предшествует
трем остальным. Группы II и III – не сравнимы.

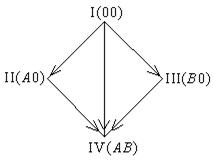
Рис. 4.2

 

Еще один пример частично упорядоченного множества слов представлен на рис. 4.3. Частичный порядок определяется транзитивным отношением “быть подсловом”: так КОН –

подслово слова КОНЬ, а оно, в свою очередь, подслово слова БРАКОНЬЕР; слово АКТ – подслово слов ТАКТ и ПРАКТИКА, которые не сравнимы.

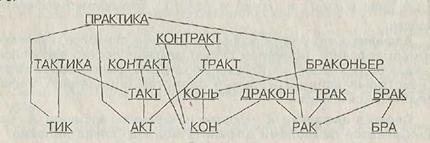
Рис. 4.3

 

Другой пример частично упорядоченного множества – трехмерные векторы, если порядок задан так: (a ₁, a ₂, a ₃) í(b ₁, b ₂, b ₃), если a ₁² + a ₂² + a ₃² < b ₁² + b ₂² + b ₃², т.е. по длине векторов; несравнимыми являются векторы одинаковой длины.

3. Для того же множества векторов можно установить и линейный порядок:
(a ₁, a ₂, a ₃) í(b ₁, b ₂, b ₃):

а) если a ₁ < b ₁;

б) если a ₁ = b ₁, a ₂ < b ₂;

в) если a ₁ = b ₁, a ₂ = b ₂, a ₃ < b ₃.

Это пример алфавитного (лексико-графического) порядка.

Алфавит – это упорядоченное множество попарно различных символов, называемых буквами алфавита. Примером служит алфавит любого европейского языка, а также алфавит из 10 арабских цифр. В компьютере клавиатура и некоторые вспомогательные средства определяют алфавит допустимых символов.

Символы алфавита в ряде случаев считаются упорядоченными (в русском алфавите: а í б,
б í в, в í г и т.д.)

Слово в алфавите – упорядоченная последовательность из символов алфавита. Слово записывается символами алфавита подряд, слева направо, без пробелов. Длина слова – число букв в нем. Иногда полезно рассматривать и пустое слово (его длина, естественно, равна 0). Натуральное число является словом в цифровом алфавите. Формула не всегда является словом
из-за нелинейного расположения символов: наличие надстрочных (показатели степени) и подстрочных (индексы переменных, основания логарифмов) символов, дробная черта, знаки радикалов и др.; однако путем некоторых соглашений она может быть приведена к записи в строку, что и применяется, например, в компьютерном программировании (так, знак возведения в степень записывается как два знака умножения подряд: формула 5**3 означает третью степень числа 5).

Алфавитное упорядочение слов определяется первым слева различающим их символом (например, слово КОНУС предшествует слову КОСИНУС, поскольку они впервые различаются в третьей букве, и буква Н предшествует С в русском алфавите). Считается также, что символ пробела предшествует любому символу алфавита – для случая, когда одно из слов является префиксом другого (например, КОН и КОНУС).

Упражнение. Проверьте, что алфавитное упорядочение натуральных чисел, имеющих одинаковое число разрядов в десятичной записи, совпадает с упорядочением их по величине
(ср. числа 28492 и 28615, но, с другой стороны, числа 28492 и 286).

4. Пусть A – частично упорядоченное множество. Элемент a Î A называется максимальным в A, если не существует элемента b Î A, для которого a < b. Элемент называется наибольшим
в A, если для всякого отличного от a элемента b Î A выполнено неравенство b < a. Симметричным образом определяются минимальный и наименьший элементы. Понятия наибольшего и максимального (соответственно, наименьшего и минимального) элементов различны (рис. 4.4). Множество на рис. 4.4, а имеет наибольший элемент p, он же является максимальным; минимальных элементов два: s и t, наименьшего нет. На рис. 4.4, б, напротив, множество имеет два максимальных элемента i и j, наибольшего нет, минимальный, он же наименьший – один: m.

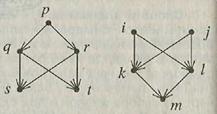
а) б)

Рис. 4.4

 

Вообще, если у множества есть наибольший (соответственно, наименьший) элемент, то только один (может не быть ни одного). Максимальных и минимальных элементов может быть несколько (может не быть совсем – в бесконечном множестве; в конечном случае – обязательно есть).

Разберем еще два примера. X 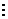Y – отношение на множестве натуральных чисел N: «Y делит X», или, по-другому, «Х является делителем числа Y» (например, 1 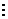5, 7 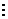35) является рефлексивным и транзитивным. Рассмотрим его на конечном множестве D ₃₀ = {1, 2, 3, 5, 6,
10, 15, 30} делителей числа 30. Отношение X 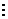Y является отношением частичного порядка (нестрогого) и изображается следующей матрицей порядка 8, содержащей 31 знак «+».

X: 1 2 3 5 6 10 15 30

Y: 1 ¦ + – – – – – – –

2 ¦ + + – – – – – –

3 ¦ + – + – – – – –

5 ¦ + – – + – – – –

6 ¦ + + + – + – – –

10 ¦ + + – + – + – –

15 ¦ + – + + – – + –

30 ¦ + + + + + + + +

Соответствующая схема с 8 вершинами должна содержать 31 связку. Однако она будет более удобна для обозрения и анализа, если исключить 8 связок-петель, изображающих рефлексивность отношения (диагональные элементы матрицы) и транзитивные связки, т.е. связки X 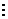Y,
если есть промежуточное число Z такое, что X 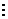Z и Z 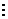Y (например, связку 3 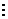30, поскольку
3 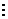15 и 15 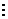30). Тогда в схеме останется 12 связок (рис. 4.5); недостающие звенья подразуме-ваются «по транзитивности». Число 1 является наименьшим, а число 30 наибольшим элементами в множестве D ₃₀.

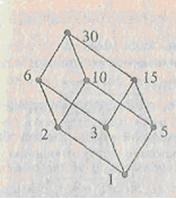
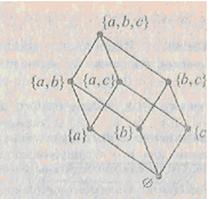
Рис. 4.5. Рис. 4.6

 

Замечание. Если исключить из D ₃₀ число 30 и рассмотреть тот же частичный порядок
на множестве D ₃₀ \ {30}, то наибольшего элемента нет, но имеются 3 максимальных элемента:
6, 10, 15; если же, напротив, исключить из D ₃₀ число 1 и рассмотреть тот же частичный порядок на множестве D ₃₀ \ {1}, то наименьшего элемента нет, но имеются 3 минимальных элемента: 2, 3, 5.

Теперь построим такую же схему для отношения включения s Í t на булеане (множестве всех подмножеств) B (M ₃) трехэлементного множества M ₃ = { a, b, c }. B (M ₃) содержит 8 элементов:

B (M ₃) = {Æ, { a }, { b }, { c }, { a, b }, { a, c }, { b, c }, { a, b, c }}.

Проверьте, что если сопоставить элементам a, b, c, соответственно числа 2, 3, 5, а операции объединения множеств – умножение соответствующих чисел (т.е., например, подмножеству { a, c } отвечает произведение 2 • 5 = 10), то матрица отношения s Í t будет точно такой же, как для отношения X 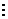Y; схемы этих двух отношений с описанными сокращениями петель и транзитив-ных связок с точностью до обозначений совпадают (рис. 4.6). Наименьшим элементом является Æ, а наибольшим – { a, b, c }.

Бинарное отношение R на множестве A и бинарное отношение S на множестве B называются изоморфными, если между A и В можно установить взаимно однозначное соответствие Г, при котором α ₁ R α ₂ → Г(α ₁) S Г(α ₂), т.е. если элементы α ₁ и α ₂ находятся в отношении R, то образы этих элементов Г(α ₁) и Г(α ₂) находятся в отношении S.

Так, частично упорядоченные множества D ₃₀ и B (M ₃) изоморфны. Рассмотренный пример допускает обобщение.

5. Отношение M Í N на булеане B (E) есть частичный порядок. Если ½ E ½ = n, т.е. множество E содержит n элементов { e ₁, e ₂,..., e_n }, то каждому подмножеству M Î B (E) соответствует
n- мерный вектор с компонентами χ _M (e_n), где χ _M – характеристическая функция множества. Совокупность всех таких векторов можно рассматривать как множество точек n -мерного арифметического пространства с координатами 0 или 1, или, по-другому, как вершины n -мерного единичного куба, обозначаемого E ⁿ, т.е. куба с ребрами единичной длины. Для n = 1, 2, 3 указанные точки представляют собой соответственно концы отрезка, вершины квадрата и куба – отсюда общее название (рис. 4.7).

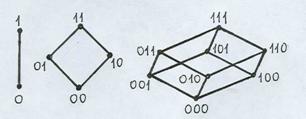
Рис. 4.7

 

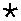Для n = 4 графическое изображение этого отношения – на рис. 4.8. Около каждой вершины 4-мерного куба указано соответствующее подмножество 4-элементного множества и четырех-мерный вектор, представляющий характеристическую функцию этого подмножества. Соединены между собой вершины, отвечающие подмножествам, которые различаются присутствием ровно одного элемента (соответствующие векторы различаются ровно в одном разряде). Наименьшим элементом является Æ, а наибольшим – { a, b, c, d }.

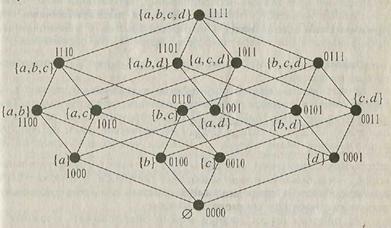
Рис. 4.8

 

На рис. 4.9 – другие наглядные представления 4-мерного куба; на рис. 4.9, а ось первой переменной ОХ направлена вверх (намеренное отклонение от вертикали, чтобы не сливались различные ребра куба): при этом 3-мерный подкуб, соответствующий Х = 0 расположен ниже, а для Х = 1 – выше.

На рис. 4.9, б та же ось ОХ направлена изнутри куба наружу: внутренний подкуб соответствует Х = 0, а внешний – Х = 1.

а) б)

Рис. 4.9

 

В Приложении 3 приведено изображение 5-мерного единичного куба.

ПРИЛОЖЕНИЯ

 

Приложение 1

Примеры решения задач

Задача 1. Проверить справедливость равенства А \ (В Ç С) = (А \ В) Ç (А \ С).

Решение. Строим диаграммы Венна отдельно для множества, заданного в левой части проверяемого равенства, и для множества в правой части (рис. 1).

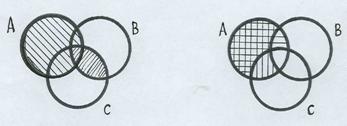
Рис. 1

 

В левой части пересечение (В Ç С) показано частой косой штриховкой, разность А \ (В Ç С) - редкой штриховкой. В правой части разность (А \ В) показана вертикальной штриховкой, разность (А \ С) – горизонтальной штриховкой, их пересечение (А \ В) Ç (А \ С) – область, заштрихованная дважды (в клеточку). Сравнение обоих рисунков показывает, что левая и правая части равенства – разные. Следовательно, равенство не верно: А \ (В Ç С) ≠ (А \ В) Ç (А \ С).

Из этих же чертежей можно заключить, что множество в левой части равенства совпадает с объединением двух разностей из правой части (А \ В) È (А \ С).

Задача 2. Опрос 100 студентов показал, что 52 пользуются домашним компьютером, 71 – мобильным телефоном, 12 – ни тем, ни другим. Сколько студентов используют оба прибора, только компьютер, только телефон?

Решение. Решение этой задачи связано с формулой числа элементов в объединении двух, вообще говоря, пересекающихся множеств: ½ А È В ½= ½ А ½ + ½ В ½ – ½ А Ç В ½.

Требуется выразить число элементов пересечения (рис. 2):

½ А È В ½= ½ А ½ + ½ В ½ – ½ А Ç В ½ Þ ½ А Ç В ½= ½ А ½ + ½ В ½ – ½ А È В ½

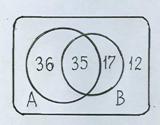
Рис. 2

 

Строим диаграмму Венна. Из условия следует, что число элементов объединения равно
100 – 12 = 88. Результаты получаем подстановкой числовых данных в формулу:

½ А È В ½= 100 – 12 = 88;

½ А Ç В ½= 52 + 71 – 88 = 35;

½ А \ В ½= 52 – 35 = 17;

½ В \ А ½= 71 – 35 = 36.

Оба прибора используют 35 студентов, только компьютер – 17, только телефон – 36.

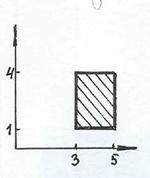
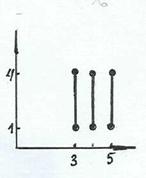
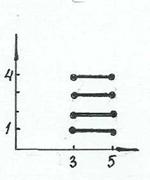
Задача 3. Что называется декартовым произведением двух множеств? Найти и показать на координатной плоскости произведение А 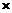В, где А = [3, 5], В = [1, 4]: А и В – множества либо дейcтвительных чисел R, либо натуральных чисел N: а) А, В Í N; б) A, B Í R; в) A Í N, B Í R;
г) A Í R, B Í N.

Решение. Декартово произведение А ´ В двух множеств – это множество всех пар (x, y), где
x Î A, y Î B.

На рисунке 3, б произведение А ´ В изображается прямоугольником, проекция которого на ось абсцисс – множество А, а проекция на ось ординат – множество В.

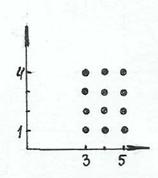
а) б) в) г)

Рис. 3

 

Если же А и В – множества целых чисел А = [3, 5], В = (1, 4); А, В Í Z, то произведение
А ´ В – прямоугольник, составленный из целочисленных точек, т.е. точек, у которых обе координаты – целые числа (рис. 3, а).

Для точек на рис. 3, в, г одна из координат дискретная, другая – непрерывная.

Задача 4. Устанавливает ли функция y = cos x взаимно однозначное соответствие между отрезками [-π/2, π/2] и [0, 1]?

Решение. Используем графическое представление основной элементарной функции y = cos x (рис. 4). На участке [-π/2, π/2] функция принимает все значения из отрезка [0, 1]. Но любое значение, кроме у = 1, функция принимает в двух точках: например, cos(-π/2) = cos(π/2) = 0.

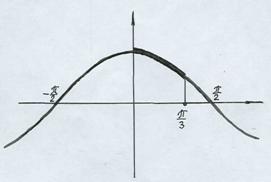
Рис. 4

 

Следовательно, взаимно однозначного соответствия на этом множестве нет.

Если же рассмотреть ту же функцию на множестве [0, π/3], то она осуществляет взаимно однозначное соответствие с отрезком [1/2, 1]. Это видно на графике.

Задача 5. Пусть f (X) = 2 ^X, g (X, Y) = X - Y. Что выражают суперпозиции h ₁(X, Y) = f (g (X, Y)), h ₂(X, Y) = g (f (Y), f (X)), h ₃(X) = f (g (X, f (X)))?

Решение. h ₁(X, Y) = f (g (X, Y)) = f (X – Y) = 2 ^X-Y.

h ₂(X, Y) = g (f (Y), f (X)) = f (Y) - f (X) = 2 ^Y - 2 ^X.

h ₃(X) = f (g (X, f (X))) = 2 ^{g (X, f (X))} = 2 ^{X - f (X)} = 2 ^{X -}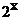

Задача 6. Построить схемы из функциональных элементов, реализующие суперпозиции
h ₂(X, Y) = g (f (X), f (Y)), h ₃(X) = f (g (X, f (X))) из предыдущей задачи.

Решение. Используются одновходовые элементы, реализующие возведение константы 2 в степень Х, и двухвходовый элемент, реализующий вычитание (рис. 5).

h ₂(X, Y) = 2 ^X - 2 ^Y h ₃(X) = 2 ^{X - .}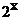

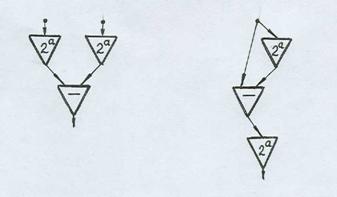
Рис. 5

 

В первом случае внешняя функция (соответственно, последний элемент в схеме) – вычитание. Во втором случае внешняя функция – возведение в степень.

Задача 7. Построить схему из функциональных элементов для вычисления объема V и полной поверхности S прямоугольного параллелепипеда, у которого длина, ширина и высота соответственно равны a, b, c.

Решение. Выражаем V и S формулами: V = a • b • c; S = 2 (a • b + a • c + b • c).

Схема (рис. 6) реализует обе формулы, причем некоторые элементы (здесь – элемент, вычисляющий произведение a • b) могут быть использованы при вычислении обеих величин.

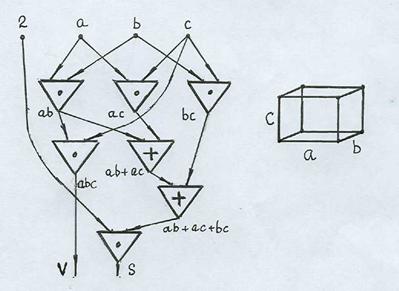
Рис. 6

Поэтому выход элемента разветвляется.

Задача 8. Какие соединения элементов данной схемы из функциональных элементов (рис. 7) являются ошибочными?

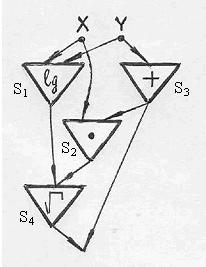
Рис. 7

Решение. 1. Элемент S ₁ – реализует одноместную функцию lg t; он не должен иметь
двух входных полюсов.

2. Элемент S ₃ – реализует двуместную функцию (s + t); он должен иметь два входных полюса.

3. На вход элемента S ₄ не должны поступать два разных значения (в данном случае с входного полюса Y и выхода элемента S ₂).

4. На единственный выход схемы не должны поступать два разных значения (в данном случае с выходов элементов S ₃ и S ₄).

Задача 9. Какую функцию реализует схема из функциональных элементов (рис. 8)?

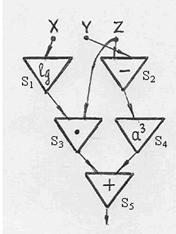
Рис. 8

Решение. 1) S ₁ = lg X;

2) S ₂ = Z – Y;

3) S ₃ = S ₁ • Z = (lg X) • Z;

4) S ₄ = (S ₂)³ = (Z – Y)³;

5) S ₅ = S ₃ + S ₄ = Z • (lg X) + (Z – Y)³.

Искомая функция – на выходе элемента S ₅.

Задача 10. x – вектор на плоскости; А (x), В (x) – одноместные алгебраические операции:
А (x) = х – b, где b = (2, 3); В (x) = 2∙ x. Какие векторы представляются суперпозициями этих операций A (A (x)), B (A (B (x))), A (B (A (x))), A (B (A (B (x)))), если х – вектор (5, 3)?

Решение. Применение операции A к вектору z - вычитание вектора (2, 3).

(А (x) = х – b = (5, 3) – (2, 3) = (3, 0).

Применение операции В к вектору z - удвоение. В (х) = 2∙ х = 2 ∙ (5, 3) = (10, 6).

Далее – применение этих операций к результату предыдущей операции. На рис. 9 – графическое представление суперпозиций.

А (А (x) = (х – b) – b = (3, 0) – (2, 3) = (1, -3);

А (В (x)) = (2 х – b) = (10, 6) – (2, 3) = (8, 3);

В (А (x)) = 2 ∙ (х – b) = 2 ∙ (3, 0) = (6, 0);

В (А (В (x))) = 2 ∙ (2 х – b) = 2 ∙ (8, 3) = (16, 6);

А (В (А (x))) = 2 ∙ (х – b) – b = (6, 0) – (2, 3) = (4, -3);

А (В (А (В (x)))) = 2 ∙ (2 х – b) – b = (16, 6) – (2, 3) = (14, 3).

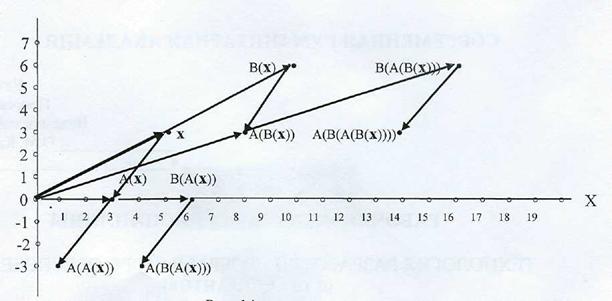
Рис. 9

 

Задача 11. Пусть R – бинарное отношение на множестве М из 12 натуральных чисел
{4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24}: «xRy, если x ¹ y и х делится на у без остатка».

Сколько пар (x, y), элементы которых находятся в отношении xRy?

Является ли отношение xRy отношением эквивалентности?

Решение. Перечислим все такие пары: (8, 4), (10, 5), (12, 4), (12, 6), (15, 5), (16, 4), (16, 8),
(18, 6), (18, 9), (20, 4), (20, 5), (20, 10), (24, 4), (24, 6), (24, 8), (24, 12). Таким образом, их число - 16. Для ответа на вторую часть вопроса нужно проверить выполнение трех свойств, которыми должно обладать отношение эквивалентности. Транзитивность отношения выполняется: если x делится на y и y делится на z, то x делится на z; однако, рефлексивность отношения не выполняется в силу условия (отношение xRy не выполняется для равных x, y); отношение xRy также несимметрично: если x делится на y, то x > y, и поэтому y не делится на x. Следовательно, xRy не есть отношение эквивалентности.

Задача 12. Является ли отношение из предыдущей задачи отношением порядка?

Решение. Уточним результаты решения предыдущей задачи. Рассматриваемое отношение xRy транзитивно, антирефлексивно (не выполняется xRх) и антисимметрично (если xRy, то не выполняется yRx). Поэтому xRy – отношение строгого порядка.

Задача 13. Является ли упорядоченным или частично упорядоченным множество М с отношением xRy на нем из задач 8, 9?

Решение. Очевидно, не все пары элементов множества М сравнимы: например, 15 и 24, 10 и 18 и другие. Поэтому М – частично упорядоченное.

Задача 14. Пусть S (x, y, z) – трехместное отношение «x = y • z» на том же множестве М, что и в задаче 8: {4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24}. Сколько троек (x, y, z), элементы которых находятся в отношении S (x, y, z)?

Решение. Все тройки, удовлетворяющие заданным условиям: (16, 4, 4), (20, 4, 5), (20, 5, 4), (24, 4, 6), (24, 6, 4); их число – 5. Заметим, что если y ¹ z, то (x, y, z) и (x, z, y) - разные тройки, но поскольку операция умножения коммутативна, то выполняется эквивалентность S (x, y, z) «

S (x, z, y), т.е. вместе с каждой тройкой S (x, y, z) условию удовлетворяет и тройка S (x, z, y).

Задача 15. Числа 83, 1906, 44, 584, 4225 упорядочить (а) по величине, (б) по алфавиту как слова в алфавите {0, 1,…, 9}, (в) по сумме цифр.

Решение. (а) 44, 83, 584, 1906, 4225;

(б) 1906, 4225, 44, 584, 83;

(в) 44, 83, 4225, 1906, 584.

Сумма цифр: 8 11 13 16 17

 

 

Приложение 2