Гуманитарная
Академия
Дистанционное образование
РУ.01;1
Рабочий учебник
Фамилия, имя, отчество обучающегося __________________________________________________
Направление подготовки ______________________________________________________________
Номер контракта _____________________________________________________________________
ДИСКРЕТНАЯ МАТЕМАТИКА
ЮНИТА 1
МНОЖЕСТВА И СООТВЕТСТВИЯ
МОСКВА 2007
Разработано Ф.Я. Ветухновским, канд. физ.-мат. наук, доц.
Под ред. Б.П. Осиленкера, д-ра физ.-мат. наук, проф.
Рекомендовано Учебно-методическим
советом в качестве учебного пособия
для студентов СГА
КУРС: ДИСКРЕТНАЯ Математика
Юнита 1. Множества и соответствия.
Юнита 2. Комбинаторика. Графы и сети.
Юнита 3. Булевы функции и предикаты.
Юнита 4. Кодирование. Конечные автоматы.
ЮНИТА 1
Содержит основные понятия и факты о структурах и задачах на конечных множествах, включая элементы теории множеств, функциональные соответствия и отношения, элементы общей алгебры. Изложение сопровождается большим количеством примеров и упражнений как в тексте, так и в Приложении 1. Разделы и упражнения, предназначенные для дополнительного изучения, выделены знаком  в начале и в конце фрагмента.
в начале и в конце фрагмента.
Для студентов Современной Гуманитарной Академии
__________________________________________________________________
© СОВРЕМЕННАЯ ГУМАНИТАРНАЯ АКАДЕМИЯ, 2007
О Г Л А В Л Е Н И Е
Стр.
ДИДАКТИЧЕСКИЙ ПЛАН.. 4
ЛИТЕРАТУРА.. 5
ПЕРЕЧЕНЬ УМЕНИЙ.. 6
ТЕМАТИЧЕСКИЙ ОБЗОР. 7
ВВЕДЕНИЕ. ПРЕДМЕТ ДИСКРЕТНОЙ МАТЕМАТИКИ.. 7
1. СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВА.. 8
1.1. Множество. Подмножество. Универсальное множество. 8
1.2. Операции над множествами: пересечение, объединение, разность, дополнение. 10
1.3. Порождающая процедура. 14
1.4. Декартово произведение множеств. 16
2. ФУНКЦИОНАЛЬНЫЕ СООТВЕТСТВИЯ.. 17
2.1. Соответствие между множествами. 17
2.2. Взаимно однозначное соответствие. 19
2.3. Числовые и точечные промежутки. 20
2.4. Суперпозиция функций. 23
2.5. Схемы из функциональных элементов. 25
3. АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ.. 28
3.1. Операции на множестве. 28
3.2. Ассоциативные и коммутативные операции. 30
3.3. Двоичная система счисления. 32
3.4. Проценты.. 35
4. БИНАРНЫЕ ОТНОШЕНИЯ.. 37
4.1. Отношения на множествах. 37
4.2. Рефлексивные, симметричные, транзитивные отношения. 39
4.3. Отношения эквивалентности. 41
4.4. Отношения порядка. 42
ПРИЛОЖЕНИЯ.. 48
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ... 57
ТРЕНИНГ УМЕНИЙ.. 63
ГЛОССАРИЙ.. 70
ДИДАКТИЧЕСКИЙ ПЛАН
Множество. Способы задания множеств. Характеристическое свойство. Универсальное множество. Операции над множествами: пересечение, объединение, разность, дополнение. Диаграммы Венна. Булеан. Разбиение множества. Порождающая процедура. Декартово произведение множеств.
Соответствие между множествами. Образ и прообраз. Функциональное соответствие. Взаимно однозначное соответствие. Эквивалентные множества. Мощность бесконечного множества. Счетные множества. Числовые промежутки: отрезок, интервал. Окрестность точки. Числовая функция. Характеристическая функция множества. Суперпозиция функций. Формула. Класс элементарных функций действительной переменной. Схемы из функциональных элементов.
Алгебраические операции на множестве. Бинарные операции. Множество, замкнутое относительно операции. Алгебра. Изоморфизм алгебр. Алгебра Кантора. Коммутативные, ассоциативные операции. Числовые функции как алгебраические операции. Позиционная система счисления. Двоичная система. Вычисления с процентами.
Отношения между элементами множества. Бинарные отношения. Матрица отношения. Многоместные отношения. Рефлексивные, симметричные отношения. Транзитивность бинарного отношения. Транзитивное замыкание отношения. Отношения эквивалентности. Отношения строгого и нестрогого порядка. Линейно упорядоченное множество. Частично упорядоченное множество. Алфавитное упорядочение. Максимальные (минимальные) и наибольшие (наименьшие) элементы. Изоморфизм отношений. Отношения включения для множеств на булеане. n -мерный единичный куб.
ЛИТЕРАТУРА
Основная
1. Акимов О.Е. Дискретная математика: логика, группы, графы. – М.: Лаборатория базовых знаний, 2001.
2. Асеев Г.Г., Абрамов О.М., Ситников Д.Э. Дискретная математика: Учебное пособие. – Ростов-н/Д.: Феникс; Харьков: Торсинг, 2003.
3. Спирина М.С., Спирин П.А. Дискретная математика. – М.: Академия, 2004.
Дополнительная
1. Верещагин Н.К., Шень А. Лекции по математической логике и теории алгоритмов. Ч. 1. Начало теории множеств. – М.: МЦНМО, 1999.
2. Дискретная математика: Энциклопедия. – М.: Большая Российская энциклопедия, 2004.
3. Козлов В.Н. Математика и информатика: Учебное пособие. – СПб.: Питер, 2004.
4. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров. ‑ 2-е изд. – М.: Энергоатомиздат, 1988.
5. Турецкий В.Я. Математика и информатика (для студентов по гуманитарным специальностям). ‑ 3-е изд. – М.: Инфра-М, 2004.
6. Шикин Е.В., Шикина Г.Е. Гуманитариям о математике. ‑ 2-е изд. – М.: УРСС (изд-во научной и учебной литературы), 2001.
ПЕРЕЧЕНЬ УМЕНИЙ
| №
п/п
| Умение
| Алгоритм
|
|
| Перевести в двоичную систему заданные деся-тичные числа
| 1. Использовать шкалу степеней основания двоичной системы – числа 2.
2. Представить заданное число в виде суммы элементов шкалы, последовательно выделяя максимально возможное слагаемое.
3. Выделить на шкале слагаемые, участвующие в разложении: им соответствует цифра 1 в двоичном представлении; отсутствующим – цифра 0
|
|
| Перевести в десятичную систему заданные двоич-ные числа
| 1. Использовать шкалу степеней основания двоичной системы – числа 2.
2. Знакам 1 в двоичном представлении заданного числа сопоставить элементы шкалы.
3. Сложить выделенные числа – степени числа 2
|
|
| Найти и показать на числовой прямой про-межутки, полученные с помощью теоретико-мно-жественных операций над числовыми проме-жутками
| 1. Изобразить заданные множества на числовой прямой.
2. Найти и показать на числовой прямой пересечение, объединение, разности заданных промежутков, дополнение до универсального множества
|
|
| Определить, какую функ-цию двух переменных W(X,Y) реализует задан-ная схема из функцио-нальных элементов
| 1. Пронумеровать элементы и сопоставить им реализуемые ими одноместные и двуместные операции.
2. Записать формулами суперпозиции промежуточных данных, последовательно выполняя соответствующие подстановки
|
|
| Определить порядок действий при вычисле-нии значения суперпози-ции элементарных функций. Построить схему из функциональных эле-ментов, реализующей функцию
| 1. Составить иерархическую схему последовательности действий:
а) определить состав переменных и констант в формуле, кото-рая задает функцию;
б) определить внешнюю операцию (функцию) и основные подформулы;
в) определить, какие из функций, составляющих суперпозицию, являются одноместными, а какие двуместными.
2. Построить схему из функциональных элементов в соответ-ствии с иерархической схемой вычисления:
а) определить совокупность используемых элементов с одним и двумя входами;
б) выделить подформулы, имеющие в суперпозиции больше одного вхождения;
в) осуществить необходимое соединение элементов
|
|
| Используя диаграммы Венна, определить число элементов подмножества данного универсального множества
| 1. Представить соотношения между множествами, заданными в условии диаграммой Венна: универсальное множество U и его подмножества в общем положении, образующие разбиение множества U.
2. Обозначить заданную в условии численность подмножеств, составленных из элементов разбиения множества U.
3. Составить численные соотношения между заданными
множествами.
4. Из полученных соотношений найти требуемое число
|
ТЕМАТИЧЕСКИЙ ОБЗОР*
СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВА
Порождающая процедура
Еще один способ задания множества связан с понятием порождающей процедуры: множество состоит из всех элементов, которые могут быть получены некоторой последовательностью операций из заданной конечной системы.
Простейший пример – задание последовательности элементов множества формулой, содержащей параметр: A = { Xk = 3 + 2(k 2 + 1)}, k = 0, 1, 2,...
Задавая различные значения параметра k, мы можем вычислять элементы множества
A: X 0 = 5, X 1 = 7, X 2 = 13 и т.д. Подобное задание может быть явным, как в данном примере, или неявным, требующим разрешения. В частности, могут использоваться возвратные, или рекуррентные соотношения, когда одни элементы множества определяются через другие.
Примеры: 1. Арифметическая прогрессия определяется заданием ее первого члена а 1, разности прогрессии d и соотношением аn +1 = аn + d для n ≥ 1. Рекуррентная формула позволяет вычислять значения а 2 = а 1 + d, а 3 = а 2 + d = а 1 +2 d, а 4 = а 3 + d = а 1 + 3 d и т.д. Можно выразить
n- й член прогрессии в явном виде: аn = а 1 + d • (n – 1).
2. Геометрическая прогрессия определяется заданием ее первого члена b 1, знаменателя прогрессии q и соотношением bn +1 = bn • q для n ≥ 1. Можно последовательно вычислять значения b 2 = b 1 • q, b 3 = b 2 • q = b 1 • q 2, b 4 = b 3 • q = = b 1 • q 3 и т.д.; n -й член этой последовательности выражается явно: bn +1 = b 1 • qn.
3. Последовательность чисел Фибоначчи задается условиями: а 1 = 1, а 2 = 1, аn = аn -1 + аn -2 для
n > 2.
Последняя формула позволяет последовательно вычислять значения а 3 = а 2 + а 1 = 1 + 1 = 2,
а 4 = а 3 + а 2 = 2 + 1 = 3, а 5 = а 4 + а 3 = 3 + 2 = 5, а 6 = а 5 + а 4 = 5 + 3 = 8,... и т.д. Выражение общего
n -го члена этой последовательности в явном виде существует, но более сложно.
Рассмотрим еще один способ задания числового множества M:
(1) 5 Î М;
(2) если а Î М, то 1/ а Î М;
(3) если а Î М, то 1 - а Î М.
Убедимся, что множество М конечно и состоит из 6 элементов, а именно
М = {5, 1/5, -4, -1/4, 4/5, 5/4}. Действительно, для каждого a, начиная со значения a = 5, есть
две возможности порождения новых элементов: операциями (2) или (3). При этом могут получаться и элементы, порожденные ранее. Так, из числа 5 операцией (2) получается 1/5, операцией (3) – число (–4), а из числа 1/5 операцией (2) – снова число 5 и т.д. Рассмотрим схему порождения (рис. 1.10), где операция (2) изображена тонкой стрелкой, а операция (3) – утолщенной. Схема показывает, что никаких других чисел процедуры (2) и (3) не дают.
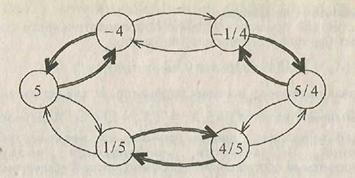
Рис. 1.10
Упражнение. Проследите, какое число в множестве М порождается, начиная с элемента 5, конечной последовательностью операций (2), (3), (3), (2), (2), (3), (2).
Если же, например, в операции (3) заменить (1 – а) на (2 – а), то порождаемое множество будет бесконечным; в частности, из числа 5 чередованием операций (2) и (3) порождается последовательность чисел 5 Þ 1/5 Þ 9/5 Þ 5/9 Þ 13/9 Þ 9/13 Þ 17/13 Þ 13/17 Þ...
ФУНКЦИОНАЛЬНЫЕ СООТВЕТСТВИЯ
Суперпозиция функций
1. Функция n переменных (n-местная функция) – это соответствие типа
A 1´ A2 ´ ... ´ An → B (другая форма записи: f (a 1, a 2,..., an) = b,
где ai Î A, b Î B). Сложение, вычитание, умножение, деление, возведение в степень являются двуместными функциями: W = x + y, W = x - y, W = x • y, W = x / y, W = xy. Двуместными функциями являются также max(x, y) и min(x, y):
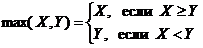
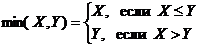
Пример. max (3, -2) = 3; min (3, -2) = -2; max (3, 3) = 3.
Функции обычно задаются вычислительными процедурами, позволяющими по значению аргументов определить значение функции. Форма этих процедур может быть различной: формулы, графики, таблицы.
В понятии формулы важным элементом является операция подстановки, или суперпозиции, позволяющая из одних функций получать другие.
Если в функцию f (X) подставить вместо аргумента Х функцию g (X), получается суперпозиция (или сложная функция) f (g (X)). В этой суперпозиции f (X) – внешняя функция, g (X) – внутренняя. Допускается также переименование переменных.
Пример. Cуперпозицией внешней функции f (x) = sin x и функции g (x) = x 2 является функция f (g (x)) = sin (g (x)) = sin(x 2); если же внешняя функция g (x), а внутренняя f (x), то суперпозицией g (f (x)) будет (f (x)2 = (sin x)2 = sin2 x.
Функции в суперпозиции могут быть не только одноместными.
Суперпозиция функций – функция, полученная из n -местной функции f (x 1, x 2, ..., xn) и системы n функций g 1, g 2,..., gn некоторой подстановкой функций g 1, g 2,..., gn во внешнюю функцию f вместо переменных и переименованиями переменных.
Примеры. 1. Cуперпозициями внешней функции f(X,Y) = X / Y и функций g 1 (X) = 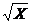 и
и
g 2 (X) = aX являются: функция 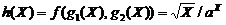 , или функция
, или функция 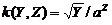 , или функция
, или функция 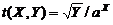 , или функция
, или функция 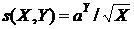 .
.
Более сложные суперпозиции этих функций: 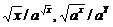 ,
, 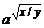 .
.
2. Примером суперпозиции одноместной функции Y = X, нульместных функций Y = const и двуместных функций Z = X + Y и Z = X ∙ Y является многочлен
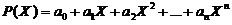 .
.
3. Суперпозициями двуместных функций min (X, Y) и max (X, Y) являются функции
трех переменных min (X, max (Y, Z)), min (X, min (Y, Z)), max (X, min (Y, Z)), max (X, max (X, Y)).
4. Класс элементарных функций есть множество всех суперпозиций основных элементарных функций (к ним относятся одноместные: степенные – хα, показательные – ах, логарифмические – logа x, тригонометрические и обратные тригонометрические, а также константы) и двуместных функций, представляющих арифметические операции: x + y, x - y, x • y, x / y.
Класс элементарных функций можно рассматривать как результат порождающей процедуры, в которой используются, исходя из основных элементарных функций, четыре арифметических действия и операция подстановки.
Замечание. Среди основных элементарных функций нет двуместной функции Z = XY.
Ее можно выразить суперпозицией других функций: логарифмической S = lg X, показательной T = 10X и умножения – в силу тождества XY = 10Y •lg Х.
Как видно из примеров, в суперпозиции функций могут измениться как сами переменные, так и их число. Заметим также, что, выполняя подстановки, мы преобразовываем формулы, выражающие функции. Формула – это выражение, описывающее суперпозицию и содержащее функциональные знаки, символы независимых переменных (аргументов) и констант (параметров). Формула с использованием скобок определяет порядок действий при вычислении значения функции. Специальные договоренности, позволяющие упростить вид формулы, освобождают ее от некоторых скобок: так в арифметике принято, что умножение и деление связывают сильнее, чем сложение и вычитание, и одночленные сомножители не заключаются в скобки.
2. Рассмотрим еще один пример функционального соответствия. Пусть U – универсальное множество; M – некоторое его подмножество, B = {0, 1} – множество из двух чисел 0 и 1.
Характеристической функцией множества M Í U – называется отображение χM: U → B, ставящее в соответствие элементам множества M единицу, а элементам дополнения 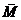 – ноль.
– ноль.
Примеры. 1. В множестве целых чисел Z для подмножества А квадратов целых чисел
(A = { x: x = k 2}) имеем: χ А (4) = χ А (25) = = 1, χ А (5) = χ А (12) = 0; для подмножества В четных чисел (В = { x: x = 2 k }) имеем: χ В (4) = χ В (12) = 1, χ В (5) = χ В (25) = 0.
2. В множестве натуральных чисел U = [0, 7] для множества М = {1, 3, 6} график функции
χ М - на рис. 2.7
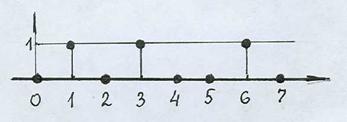
Рис. 2.7
Легко проверяются следующие свойства характеристической функции множеств, получаемых из множеств M, N операциями пересечения, объединения, разности и дополнения:
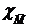 = 1 - χ M; χ M ∩ N = χ M • χ N; χ M È N = χ M + χ N - χ M • χ N; χ M \ N = χ M - χ M • χ N.
= 1 - χ M; χ M ∩ N = χ M • χ N; χ M È N = χ M + χ N - χ M • χ N; χ M \ N = χ M - χ M • χ N.
Булеаном В (U) называется множество всех подмножеств множества U.
Если U - конечное множество, ½ U ½ = n, и его элементы занумерованы числами 1, 2,..., n, то каждому подмножеству M Í U соответствует n -мерный вектор из нулей и единиц с компонентами χ M (en), где χ M – характеристическая функция множества М. Совокупность всех таких характеристических векторов можно рассматривать как множество точек n -мерного арифметического пространства с координатами 0 или 1. Вместе они образуют n -мерный единичный куб.
Если U – конечное множество и число его элементов ½ U ½ равно n, то число элементов булеана В (U) равно числу 2 n характеристических векторов. Подробнее об этом – в разделе «Элементы комбинаторики» Юниты 2.
АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ
Операции на множестве
1. Пример однозначного соответствия между множествами чисел X и Y – функция y = f (x). Функция двух переменных z = f (x, y) сопоставляет числовое значение z паречисел (x, y).
Функцию можно рассматривать как операцию над элементами числового множества: так, одноместная операция y = 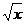 преобразует число 9 в число 3, число 5 - в число
преобразует число 9 в число 3, число 5 - в число 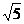 = 2,236... Аналогично, двуместная операция z = x ∙ y преобразует пару чисел (3, 5) в число 15, другая операция z = x + y сопоставляет той же паре число 8.
= 2,236... Аналогично, двуместная операция z = x ∙ y преобразует пару чисел (3, 5) в число 15, другая операция z = x + y сопоставляет той же паре число 8.
Общее понятие алгебраической операции на множестве: элементам множества М сопоставляется элемент того же или другого множества. Операции можно разделить на одноместные, двуместные (называемые также бинарными), трехместные и т.д. Общее обозначение бинарной операции: φ (a, b) или a φ b. Арифметические действия сложения a + b, вычитания a – b, умножения a · b, деления a / b, возведения в степень ab – бинарные операции (в то же время, операция возведения числа в квадрат или в куб, т.е. в конкретную степень – одноместные операции). Двуместная операция скалярного произведения сопоставляет двум векторам число. Операции над множествами: объединение, пересечение, разность – двуместные; операция дополнения – одноместная. Также двуместной является операция декартова произведения
двух множеств А ´ В.
Операции преобразований плоскости – сжатия, растяжения, отражения, повороты – переводят одни точки плоскости в другие. Алгебраическая операция может применяться и к элементам разных множеств: пример – умножение вектора на число: 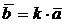 .
.
2. Множество М называется замкнутым относительно операции φ, если применение операции не выводит за пределы множества М, т.е. всякий результат операции над элементами множества М также принадлежит М.
Примеры. 1. Множества действительных, рациональных, целых чисел замкнуты относительно операций сложения (это значит, что, например, сумма двух целых чисел – целое число), а также вычитания, умножения, причем первые два множества замкнуты и относительно операции деления (исключая деление на 0). Множество целых чисел не замкнуто относительно деления.
2. Множество четных целых чисел замкнуто относительно операций сложения и умножения: сумма и произведение четных чисел также четны. Напротив, множество нечетных чисел не замкнуто относительно операции сложения.
Упражнение. 1. Замкнуто ли относительно вычитания множество четных чисел (т.е. всегда ли четна сумма четных чисел)?
2. Замкнуто ли относительно умножения множество нечетных чисел (т.е. всегда ли нечетно произведение нечетных чисел)?
3. Определите, замкнуто ли относительно операции извлечения квадратного корня множество: а) действительных чисел; б) положительных действительных чисел; в) целых чисел.
4. Тот же вопрос для операции возведения числа в квадрат.
Система А = (L; Ω), состоящая из множества L и набора операций Ω = { φ 1, φ 2,..., φk }, действующих на множестве L, называют алгеброй (так что алгебра – не только математическая дисциплина, но и вполне определенная структура). Множество L (оно должно быть замкнутым относительно операций системы Ω) называется носителем, а система операций Ω – сигнатурой алгебры А.
Примеры. 1. (R; +, •), (N; +, •), (Z; +, •), – алгебры на множестве соответственно, действительных, натуральных и целых чисел с операциями сложения и умножения (при сложении и умножении чисел каждого из этих множеств результат принадлежит тому же множеству).
2. (F; D) и (FЭ; D), где F – множество дифференцируемых функций действительной переменной, FЭ - множество элементарных функций; D – оператор дифференцирования, ставящий в соответствие каждой функции ее производную.
3. Изоморфизмом двух алгебр А = (L; φ 1, φ 2,..., φk) и В = (M; ψ 1, ψ 2,..., ψk), называется взаимно однозначное соответствие Г между множествами L = { l } и M = { m } и между операциями φi и ψi, при котором выполнено:
Г(φi (l)) = ψi (Г(l)) для всех l, φi, ψi.
Подчеркнем, что изоморфизм – это не просто взаимно однозначное соответствие (его – для конечных множеств – можно установить между любыми двумя множествами с одинаковым числом элементов). Смысл этого понятия состоит в том, что если выполнить в алгебре A какие-либо операции над определенными элементами множества L и соответствующие операции в алгебре B над соответствующими элементами множества M, то результаты операций также будут соответствовать друг другу.
Примеры. 1. Алгебры (Z; +) и (Z 3; +), где Z 3 – множество целых чисел, кратных трем, изоморфны, в силу соответствия Г = n → 3 n. Так, например, сложению 5 + 8 = 13 будет соответствовать сложение 15 + 24 = 39, что можно проиллюстрировать схемой
n: 5 + 8 = 13;
3 n: 15 + 24 = 39.
2. Алгебры (R +; •) и (R; +), где R + - множество положительных действительных чисел, изоморфны в силу соответствия Г = a → log a (ввиду тождества log ab = log a + log b). Это также проиллюстрируем схемой
a: 8 • 64 = 512;
↓log2 ↓log2 ↓log2 ↓log2 (3 = log2 8; 6 = log2 64; 9 = log2 512);
log a: 3 + 6 = 9.
В этом примере только для наглядности участвуют целые степени числа 2, при этом их двоичные логарифмы - целые числа.
Противоположный пример: алгебры (Z; +) и (Z 2; +), где Z 2 – множество целочисленных двумерных векторов, не изоморфны. Хотя оба множества Z и Z 2 – счетны, т.е. между ними можно (многими способами) установить взаимно однозначное соответствие, но не удастся сделать это так, чтобы сумма векторов, поставленных в соответствие двум числам, всегда соответствовала сумме этих чисел. Конечно, это требует доказательства, но мы его здесь не приводим.
Особое значение имеет следующий пример. Булеан В (U), очевидно, является замкнутым относительно операций объединения, пересечения и дополнения: результат любой из этих операций над подмножествами универсального множества U - также одно из его подмножеств. Система В (U) с операциями (È, ∩, ‾‾) называется алгеброй множеств на U, или алгеброй Кантора.
Алгебры (U; È) и (U; ∩) на булеане В (U) произвольного множества U изоморфны. Изоморфизм устанавливается соответствием Г(L) = 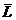 , L Í U.
, L Í U.
В самом деле, Г(L 1 È L 2) = 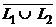 = [в силу закона де Моргана] =
= [в силу закона де Моргана] = 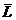 1 ∩
1 ∩ 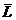 2 = Г(L 1) ∩ Г(L 2).
2 = Г(L 1) ∩ Г(L 2).
Как видно из рассмотренных примеров, если алгебры А и В изоморфны, то элементы и операции В можно переименовать так, что В совпадет с А. Из основного равенства в опреде-лении изоморфизма следует, что любое эквивалентное соотношение в алгебре А сохраняется в каждой изоморфной ей алгебре В. Это позволяет, получив такие соотношения в алгебре А, автоматически распространить их на все алгебры, изоморфные А. Распространенное в математике выражение «рассматривать объекты с точностью до изоморфизма» означает, что рассматриваются только те свойства объектов, которые сохраняются при изоморфизме, т.е. являются общими для всех изоморфных объектов.
Установление изоморфизма между какими-либо системами имеет большое практическое значение. Оно сродни точному переводу на другой язык описания явлений. Когда, например, аналитическая геометрия устанавливает соотношения между геометрическими объектами – линиями или поверхностями и их аналитическими представлениями в виде уравнений, или в курсе математического анализа мы выясняем геометрический смысл производной, дифференциала или интеграла, мы получаем возможность выбирать и использовать при исследованиях и в прикладных задачах наиболее удобное для данного случая представление. В некоторых задачах изоморфизм систем служит основанием для моделирования объектов и их взаимодействия.
Двоичная система счисления
1. Хорошо известен способ записи чисел в десятичной системе. Эта система называется позиционной десятичной, потому что натуральное число представляется словом в алфавите из десяти арабских цифр Ц10= [0, 1, 2, 3,..., 9], причем знаки числа изображают различные его составляющие в зависимости от разряда – позиции в числе и служат коэффициентами при степенях основания – числа 10. Например, 48087 = 40000 + 8000 + 80 + 7 = 4 × 104 + 8 × 103 +
+ 0 × 102 + 8 ×101 + 7 × 100, и цифра 8 во втором разряде изображает число 80, а та же цифра в четвертом разряде – число 8000. Позиционная система исторически вытеснила другие способы представления чисел благодаря удобствам использования, главным образом, из-за достаточно простых алгоритмов арифметических действий над многозначными числами, которые сводятся к действиям над однозначными числами. При этом используются таблица сложения, т.е. правила типа 3 + 6 = 9, 4 + 8 = 12 и т.п., общеизвестная таблица умножения и – при сложении и умножении столбиком – правила переноса десятков в старшие разряды («шестью девять – пятьдесят четыре; четыре пишем, пять в уме»). Отметим, что при сложении столбиком справа налево двух слагаемых каждый очередной знак суммы определяется знаками слагаемых в этом разряде с учетом знака переноса (0, если сумма не превышает 9, или 1, если сумма двузначная). При умножении многозначных чисел A ´ B столбиком каждое умножение A на однозначное число, каким является очередной разряд числа B, также сопровождается переносом числа десятков в следующий разряд. Далее следует сложение нескольких многозначных чисел, записываемых со сдвигом. При сложении большого количества чисел может возникать накопление знаков переноса.
Важно заметить, что как при сложении, так и при умножении каждый знак результата
зависит от знаков слагаемых/сомножителей, находящихся в том же разряде и правее, и не зависит
от старших разрядов (находящихся левее). Так, младший разряд результата является функцией
двух однозначных чисел – младших разрядов слагаемых/сомножителей. Второй справа разряд
есть функция четырех однозначных переменных – знаков двух младших разрядов
слагаемых/сомножителей и т.д.
2. Таким же образом, только много проще, устроена двоичная система счисления. Числа представляются словами в алфавите Ц2= [0, 1], и например, 1101001012= 28 + 27 + 25 + 22 + 20 =
= (256 + 128 + 32 + 4 + 1)10= 42110 (подстрочные индексы 2 и 10 обозначают, что одно число записано в двоичной, а другое – в десятичной системе). Вот двоичные представления нескольких первых натуральных чисел (в левом столбце – десятичные; в правом – двоичные):
| 0 - 0
| 5 - 101
| 11 - 1011
| 16 - 10000
|
| 1 - 1
| 6 - 110
| 12 - 1100
| 17 – 10001
|
| 2 - 10
| 7 - 111
| 13 - 1101
| 18 - 10010
|
| 3 - 11
| 8 - 1000
| 14 - 1110
| 19 – 10011
|
| 4 - 100
| 9 - 1001
| 15 - 1111
| и т.д.
|
Подобно тому, как в десятичной системе счисления целые степени основания
системы 10 записываются единицей с нулями, а число на 1 меньшее – 99...9, в двоичной системе число 10...0 с k нулями изображает число 2 k (2, 4, 8, 16,...), а число 11...1 из k единиц
равно 2 k – 1 (1, 3, 7, 15,...).
Таблица сложения для двоичных чисел чрезвычайно проста:
0 + 0 = 0; 0 + 1 = 1 + 0 = 1; 1 + 1 = 10.
Таблица умножения еще проще: 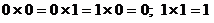 .
.
Их можно представить и таблицами с двумя входами:

Отсюда – простота действий над многозначными числами, хотя двоичная запись числа длиннее десятичной более чем втрое. Предыдущий пример демонстрирует перевод двоичного числа в десятичное. Для этого, так же как и для обратного перехода, полезно знать значения шкалы целых степеней числа 2: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 и т.д. Каждое целое число можно однозначно представить в виде суммы различных целых степеней числа 2.
Например, 179 = 128 + 51 = 27 + 32 + 19 = = 27 + 25 + 16 + 3 = 27 + 25 + 24 + 2 + 1, поэтому двоичной записью десятичного числа 17910 будет 101100112 (слагаемые 27, 25, 24, 21, 20 входят в сумму 179 с коэффициентом 1; остальные степени числа 2: 26, 23, 22 – с коэффициентом 0). Ниже – примеры арифметических действий над двоичными числами (параллельно приведены действия с теми же числами в десятичной записи).

Как видим, сложение, вычитание и умножение многозначных двоичных чисел производится так же, как и десятичных, в частности, в обеих системах k -й знак результата арифметических действий зависит от k -х знаков слагаемых (соответственно, сомножителей) и знаков младших разрядов. Однако накопление знаков переноса при сложении возникает здесь значительно чаще: каждые две единицы дают перенос одной единицы в следующий – старший – разряд, сложение четырех единиц дает две единицы переноса, т.е. перенос одной единицы на два разряда влево.
Деление двоичных чисел «столбиком» также намного проще, чем в десятичной системе, поскольку не приходится подбирать очередной знак частного: остаток не должен быть меньше делителя, – в этом случае знак частного 1; в противном случае, как и для десятичных чисел, он равен 0, и нужно приписать к остатку (снести) очередной разряд делимого.
3. Двоичные числа можно рассматривать и как упорядоченные наборы цифр, или, по-другому, слова в двухбуквенном алфавите В = {0, 1}. При этом иногда добавляют нули слева от значащих цифр, например, чтобы уравнять длину двух таких наборов, и можно было бы считать оба набора векторами многомерного арифметического пространства, а сами двоичные цифры - компонентами этих векторов. Тогда результат арифметических действий над двоичными числами также двоичный вектор, возможно иной (для сложения и умножения – большей) размерности.
Среди алгебраических операций над двоичными векторами можно выделить поразрядные операции, например, поразрядное умножение: k -й знак результата равен произведению k -х знаков сомножителей. Другая операция – поразрядная сумма по модулю 2: k -й знак результата равен остатку от деления на два обычной арифметической суммы k -х знаков слагаемых.
Таблица этой операции для однозначных двоичных чисел a Å b:
Значения a Å b равны 1, если ровно одно из слагаемых равно 1, т.е. если оба слагаемых различны, и равны 0, если оба слагаемых одинаковы.
Если рассматривать двоичный n -мерный вектор 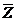 как представление характеристической функции χ M упорядоченного подмножества М n -элементного универсального множества
как представление характеристической функции χ M упорядоченного подмножества М n -элементного универсального множества
(k -я компонента вектора равна 1, если k -й элемент универсального множества принадлежит множеству М), то поразрядное произведение 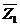 •
• 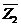 двух таких векторов
двух таких векторов 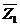 и
и 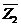 представляет характеристическую функцию χ M∩N пересечения М 1 ∩ М 2 соответствующих множеств М 1 и М 2, равную χM • χN, а поразрядная сумма по модулю 2 - вектор
представляет характеристическую функцию χ M∩N пересечения М 1 ∩ М 2 соответствующих множеств М 1 и М 2, равную χM • χN, а поразрядная сумма по модулю 2 - вектор 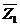 Å
Å 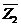 - характеристическую функцию χ M Δ N симметрической разности М 1 Δ М 2 тех же множеств, равную χM Å χN.
- характеристическую функцию χ M Δ N симметрической разности М 1 Δ М 2 тех же множеств, равную χM Å χN.
4. Рассмотрим для каждого n (n = 1, 2, 3,...) последовательность Dn всех двоичных наборов длины n в алфавитном порядке, записанную в столбик. На рис. 3.2 - таблицы D 1, D 2, D 3.

Рис. 3.2
Если эти наборы из нулей и единиц прочитать как двоичные числа, игнорируя начальные нули, то это будет начальный отрезок натурального ряда от 0 до 2 n -1. Для любого k < 2 n- 1 сумма
k -го от начала числа dk и k -го от к





 в начале и в конце фрагмента.
в начале и в конце фрагмента.
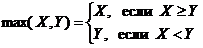
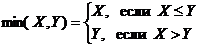
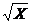 и
и 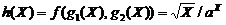 , или функция
, или функция 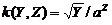 , или функция
, или функция 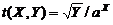 , или функция
, или функция 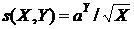 .
.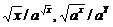 ,
, 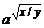 .
.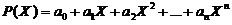 .
.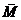 – ноль.
– ноль.
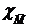 = 1 - χ M; χ M ∩ N = χ M • χ N; χ M È N = χ M + χ N - χ M • χ N; χ M \ N = χ M - χ M • χ N.
= 1 - χ M; χ M ∩ N = χ M • χ N; χ M È N = χ M + χ N - χ M • χ N; χ M \ N = χ M - χ M • χ N.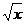 преобразует число 9 в число 3, число 5 - в число
преобразует число 9 в число 3, число 5 - в число 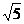 = 2,236... Аналогично, двуместная операция z = x ∙ y преобразует пару чисел (3, 5) в число 15, другая операция z = x + y сопоставляет той же паре число 8.
= 2,236... Аналогично, двуместная операция z = x ∙ y преобразует пару чисел (3, 5) в число 15, другая операция z = x + y сопоставляет той же паре число 8.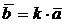 .
.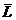 , L Í U.
, L Í U.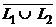 = [в силу закона де Моргана] =
= [в силу закона де Моргана] = 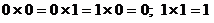 .
.

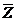 как представление характеристической функции χ M упорядоченного подмножества М n -элементного универсального множества
как представление характеристической функции χ M упорядоченного подмножества М n -элементного универсального множества 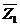 •
• 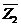 двух таких векторов
двух таких векторов 


