Суперпозиции одноместных и двуместных функций удобно представлять в виде символических схем вычисления. Внутренние и внешние одноместные и двуместные функции изображаются функциональными элементами с одним или двумя входами (по числу аргументов) и одним выходом. Можно рассматривать, конечно, функции и соответственно элементы с большим числом аргументов. Элемент, которому приписана функция, графически представляет собой треугольник; входные полюсы – на основании, выход – вершина треугольника (рис. 2.8). Выходы элементов могут присоединяться к входам других элементов, означая подстановку внутренней функции во внешнюю.

Рис. 2.8
Определим индуктивно понятие вычислительной схемы (обратите внимание на то, как строится определение: вводятся некоторые начальные объекты, и задается способ образования из них других, более сложных объектов, т.е. порождающий процесс; такой тип определения называется индуктивным).
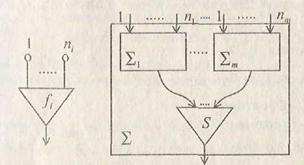
Пусть имеется конечное множество объектов { Si }, которые будем называть структурными элементами. Каждый элемент Si имеет некоторое количество ni входов и 1 выход. Сеть из структурных элементов определяется следующим образом.
1. Каждый элемент Si является сетью, входы и выходы сети – это соответственно, входы и выходы элемента Si (рис. 2.9, а).
а) б)
Рис. 2.9
2. Пусть S – структурный элемент с m входами и å1, å2,..., å m – сети из структурных элементов. Тогда соединение å этих сетей, изображенное на рис. 2.9, б, является сетью: ее
входы – объединение входов сетей å1, å2,..., å m, выходы сетей å1, å2,..., å m присоединены в определенном порядке к входам элемента S. Заметим, что у сетей å I и åj могут быть пересекающиеся множества входов. Выходом сети å считается выход элемента S.
Сети å1, å2,..., å m называются подсетями, а их элементы вместе с элементом S – элементами сети å.
Схемой из функциональных элементов называется сеть, элементам которой приписаны (сопоставлены) функции, так что элементу S с k входами соответствует k -местная функция
f (x 1, x 2,..., xk). Будем говорить, что элемент S реализует функцию f (x 1, x 2,..., xk). Значения выходов одних элементов служат значениями аргументов для функций других элементов в соответствии со структурой схемы, причем для элементов, реализующих некоммутативные операции, важен порядок аргументов. Если функция fS, сопоставленная некоторому элементу S, не определена на каком-либо наборе значений своих аргументов, то на этом наборе не определены как значения выхода S,таки все функции элементов, на входы которых поступают значения fS. Рис. 2.10 демонстрирует разницу в реализуемых функциях при различном порядке присоединения.
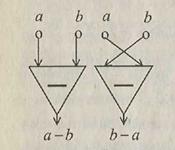
Рис. 2.10
На рис. 2.11 – пример схемы, состоящей из 6 элементов, реализующих 4 функции: f 1, f 3– двуместные; f 2, f 4– одноместные (элементы f 1, f 3присутствуют дважды, причем в одном случае на оба входа элемента f 1подаются одинаковые значения). Независимо от реального содержания
f 1- f 4схема реализует вполне определенную сложную суперпозицию
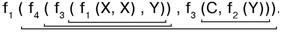
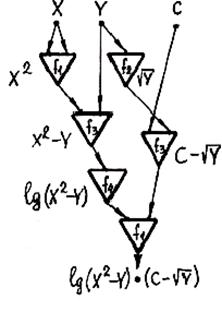
Рис. 2.11
Для удобства чтения сложной формулы показаны соответствующие друг другу левая и правая скобки.
Если, например, элементы f 1¸ f 4 вычисляют конкретные числовые функции:
f 1 (Х, Y) = X ∙ Y;
f 2 (Х) = 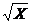 ;
;
f 3 (Х, Y) = X – Y;
f 4 (Х) = lg X,
то схема реализует функцию двух переменных Z (X, Y) = ( lg (X 2- Y)) ∙ (C - 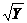 ), что и обозначено
), что и обозначено
на рис. 2.11.
Вычислительная процедура определяется, вообще говоря, неоднозначно и зависит от того, какие функции приняты за исходные. Так, функция 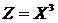 может рассматриваться как элементарная функция (рис. 2.12, а), реализуемая одним элементом; как каскад из двух умножений
может рассматриваться как элементарная функция (рис. 2.12, а), реализуемая одним элементом; как каскад из двух умножений 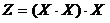 (рис. 2.12, б) в виде двух элементов умножения; как частный случай двуместной функции Z = XY при Y = 3 (рис. 2.12, в). В последнем случае в качестве аргумента участвует функция-константа g = 3.
(рис. 2.12, б) в виде двух элементов умножения; как частный случай двуместной функции Z = XY при Y = 3 (рис. 2.12, в). В последнем случае в качестве аргумента участвует функция-константа g = 3.
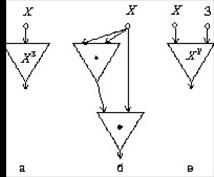
Рис. 2.12
Схема из функциональных элементов соответствует формуле, и если одну и ту же функцию представить разными формулами, то она может быть реализована различными схемами (рис. 2.13, а и 2.13, б).
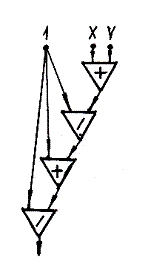
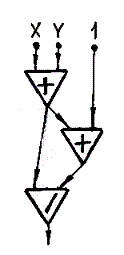
а) б)
Рис. 2.13
Пример. Формулу Z = 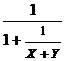 реализует схема рис. 2.13, а, а тождественную ей
реализует схема рис. 2.13, а, а тождественную ей
(при X, Y > 0) формулу 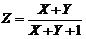 – схема рис. 2.13, б.
– схема рис. 2.13, б.
Упражнение: построить схемы вычисления функций действительных переменных, используя элементы, реализующие основные элементарные функции и арифметические действия:
а) Z(X, Y) = 2 Y-2X • 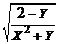 ;
;
б) W (X, Y, Z) = sin(X – Z / Y 2).
АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ
Операции на множестве
1. Пример однозначного соответствия между множествами чисел X и Y – функция y = f (x). Функция двух переменных z = f (x, y) сопоставляет числовое значение z паречисел (x, y).
Функцию можно рассматривать как операцию над элементами числового множества: так, одноместная операция y = 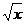 преобразует число 9 в число 3, число 5 - в число
преобразует число 9 в число 3, число 5 - в число 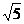 = 2,236... Аналогично, двуместная операция z = x ∙ y преобразует пару чисел (3, 5) в число 15, другая операция z = x + y сопоставляет той же паре число 8.
= 2,236... Аналогично, двуместная операция z = x ∙ y преобразует пару чисел (3, 5) в число 15, другая операция z = x + y сопоставляет той же паре число 8.
Общее понятие алгебраической операции на множестве: элементам множества М сопоставляется элемент того же или другого множества. Операции можно разделить на одноместные, двуместные (называемые также бинарными), трехместные и т.д. Общее обозначение бинарной операции: φ (a, b) или a φ b. Арифметические действия сложения a + b, вычитания a – b, умножения a · b, деления a / b, возведения в степень ab – бинарные операции (в то же время, операция возведения числа в квадрат или в куб, т.е. в конкретную степень – одноместные операции). Двуместная операция скалярного произведения сопоставляет двум векторам число. Операции над множествами: объединение, пересечение, разность – двуместные; операция дополнения – одноместная. Также двуместной является операция декартова произведения
двух множеств А ´ В.
Операции преобразований плоскости – сжатия, растяжения, отражения, повороты – переводят одни точки плоскости в другие. Алгебраическая операция может применяться и к элементам разных множеств: пример – умножение вектора на число: 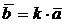 .
.
2. Множество М называется замкнутым относительно операции φ, если применение операции не выводит за пределы множества М, т.е. всякий результат операции над элементами множества М также принадлежит М.
Примеры. 1. Множества действительных, рациональных, целых чисел замкнуты относительно операций сложения (это значит, что, например, сумма двух целых чисел – целое число), а также вычитания, умножения, причем первые два множества замкнуты и относительно операции деления (исключая деление на 0). Множество целых чисел не замкнуто относительно деления.
2. Множество четных целых чисел замкнуто относительно операций сложения и умножения: сумма и произведение четных чисел также четны. Напротив, множество нечетных чисел не замкнуто относительно операции сложения.
Упражнение. 1. Замкнуто ли относительно вычитания множество четных чисел (т.е. всегда ли четна сумма четных чисел)?
2. Замкнуто ли относительно умножения множество нечетных чисел (т.е. всегда ли нечетно произведение нечетных чисел)?
3. Определите, замкнуто ли относительно операции извлечения квадратного корня множество: а) действительных чисел; б) положительных действительных чисел; в) целых чисел.
4. Тот же вопрос для операции возведения числа в квадрат.
Система А = (L; Ω), состоящая из множества L и набора операций Ω = { φ 1, φ 2,..., φk }, действующих на множестве L, называют алгеброй (так что алгебра – не только математическая дисциплина, но и вполне определенная структура). Множество L (оно должно быть замкнутым относительно операций системы Ω) называется носителем, а система операций Ω – сигнатурой алгебры А.
Примеры. 1. (R; +, •), (N; +, •), (Z; +, •), – алгебры на множестве соответственно, действительных, натуральных и целых чисел с операциями сложения и умножения (при сложении и умножении чисел каждого из этих множеств результат принадлежит тому же множеству).
2. (F; D) и (FЭ; D), где F – множество дифференцируемых функций действительной переменной, FЭ - множество элементарных функций; D – оператор дифференцирования, ставящий в соответствие каждой функции ее производную.
3. Изоморфизмом двух алгебр А = (L; φ 1, φ 2,..., φk) и В = (M; ψ 1, ψ 2,..., ψk), называется взаимно однозначное соответствие Г между множествами L = { l } и M = { m } и между операциями φi и ψi, при котором выполнено:
Г(φi (l)) = ψi (Г(l)) для всех l, φi, ψi.
Подчеркнем, что изоморфизм – это не просто взаимно однозначное соответствие (его – для конечных множеств – можно установить между любыми двумя множествами с одинаковым числом элементов). Смысл этого понятия состоит в том, что если выполнить в алгебре A какие-либо операции над определенными элементами множества L и соответствующие операции в алгебре B над соответствующими элементами множества M, то результаты операций также будут соответствовать друг другу.
Примеры. 1. Алгебры (Z; +) и (Z 3; +), где Z 3 – множество целых чисел, кратных трем, изоморфны, в силу соответствия Г = n → 3 n. Так, например, сложению 5 + 8 = 13 будет соответствовать сложение 15 + 24 = 39, что можно проиллюстрировать схемой
n: 5 + 8 = 13;
3 n: 15 + 24 = 39.
2. Алгебры (R +; •) и (R; +), где R + - множество положительных действительных чисел, изоморфны в силу соответствия Г = a → log a (ввиду тождества log ab = log a + log b). Это также проиллюстрируем схемой
a: 8 • 64 = 512;
↓log2 ↓log2 ↓log2 ↓log2 (3 = log2 8; 6 = log2 64; 9 = log2 512);
log a: 3 + 6 = 9.
В этом примере только для наглядности участвуют целые степени числа 2, при этом их двоичные логарифмы - целые числа.
Противоположный пример: алгебры (Z; +) и (Z 2; +), где Z 2 – множество целочисленных двумерных векторов, не изоморфны. Хотя оба множества Z и Z 2 – счетны, т.е. между ними можно (многими способами) установить взаимно однозначное соответствие, но не удастся сделать это так, чтобы сумма векторов, поставленных в соответствие двум числам, всегда соответствовала сумме этих чисел. Конечно, это требует доказательства, но мы его здесь не приводим.
Особое значение имеет следующий пример. Булеан В (U), очевидно, является замкнутым относительно операций объединения, пересечения и дополнения: результат любой из этих операций над подмножествами универсального множества U - также одно из его подмножеств. Система В (U) с операциями (È, ∩, ‾‾) называется алгеброй множеств на U, или алгеброй Кантора.
Алгебры (U; È) и (U; ∩) на булеане В (U) произвольного множества U изоморфны. Изоморфизм устанавливается соответствием Г(L) = 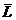 , L Í U.
, L Í U.
В самом деле, Г(L 1 È L 2) = 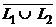 = [в силу закона де Моргана] =
= [в силу закона де Моргана] = 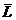 1 ∩
1 ∩ 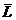 2 = Г(L 1) ∩ Г(L 2).
2 = Г(L 1) ∩ Г(L 2).
Как видно из рассмотренных примеров, если алгебры А и В изоморфны, то элементы и операции В можно переименовать так, что В совпадет с А. Из основного равенства в опреде-лении изоморфизма следует, что любое эквивалентное соотношение в алгебре А сохраняется в каждой изоморфной ей алгебре В. Это позволяет, получив такие соотношения в алгебре А, автоматически распространить их на все алгебры, изоморфные А. Распространенное в математике выражение «рассматривать объекты с точностью до изоморфизма» означает, что рассматриваются только те свойства объектов, которые сохраняются при изоморфизме, т.е. являются общими для всех изоморфных объектов.
Установление изоморфизма между какими-либо системами имеет большое практическое значение. Оно сродни точному переводу на другой язык описания явлений. Когда, например, аналитическая геометрия устанавливает соотношения между геометрическими объектами – линиями или поверхностями и их аналитическими представлениями в виде уравнений, или в курсе математического анализа мы выясняем геометрический смысл производной, дифференциала или интеграла, мы получаем возможность выбирать и использовать при исследованиях и в прикладных задачах наиболее удобное для данного случая представление. В некоторых задачах изоморфизм систем служит основанием для моделирования объектов и их взаимодействия.








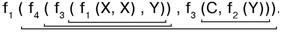

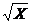 ;
;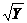 ), что и обозначено
), что и обозначено 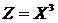 может рассматриваться как элементарная функция (рис. 2.12, а), реализуемая одним элементом; как каскад из двух умножений
может рассматриваться как элементарная функция (рис. 2.12, а), реализуемая одним элементом; как каскад из двух умножений 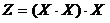 (рис. 2.12, б) в виде двух элементов умножения; как частный случай двуместной функции Z = XY при Y = 3 (рис. 2.12, в). В последнем случае в качестве аргумента участвует функция-константа g = 3.
(рис. 2.12, б) в виде двух элементов умножения; как частный случай двуместной функции Z = XY при Y = 3 (рис. 2.12, в). В последнем случае в качестве аргумента участвует функция-константа g = 3.


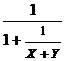 реализует схема рис. 2.13, а, а тождественную ей
реализует схема рис. 2.13, а, а тождественную ей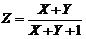 – схема рис. 2.13, б.
– схема рис. 2.13, б.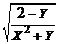 ;
;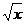 преобразует число 9 в число 3, число 5 - в число
преобразует число 9 в число 3, число 5 - в число 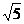 = 2,236... Аналогично, двуместная операция z = x ∙ y преобразует пару чисел (3, 5) в число 15, другая операция z = x + y сопоставляет той же паре число 8.
= 2,236... Аналогично, двуместная операция z = x ∙ y преобразует пару чисел (3, 5) в число 15, другая операция z = x + y сопоставляет той же паре число 8.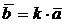 .
.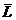 , L Í U.
, L Í U.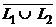 = [в силу закона де Моргана] =
= [в силу закона де Моргана] = 


