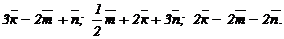Определение: Векторы, направления которых противоположны, называются противоположно направленными.
Определение: Векторы, направления которых противоположны, а длины равны, называются противоположными.
Замечание: Если 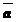 и
и 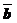 противоположные векторы, то пишут
противоположные векторы, то пишут 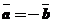 или
или 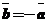 .
.
Рис. 1. Рис. 2.
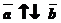
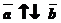 и |а | = |b |
и |а | = |b |
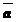 и
и 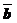
 и
и 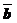
Противоположно направленные противоположные векторы
Векторы
- Действия над векторами на плоскости
2.1. 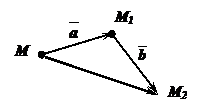 Сложение векторов.
Сложение векторов.
Пусть вектор  отображает точку М на точку М1; вектор
отображает точку М на точку М1; вектор 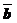 отображает точку М1 на точку М2 . Тогда существует вектор, отображающий точку М на точку М2.
отображает точку М1 на точку М2 . Тогда существует вектор, отображающий точку М на точку М2.
Определение: Пусть вектор  отображает точку М на точку М1; вектор
отображает точку М на точку М1; вектор 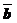 отображает точку М1 на точку М2 . Вектор, отображающий точку М на точку М2 , называется композицией векторов
отображает точку М1 на точку М2 . Вектор, отображающий точку М на точку М2 , называется композицией векторов 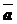 и
и 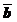 .
.
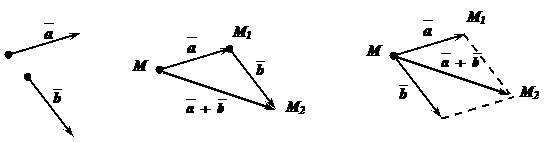 Определение: Суммой
Определение: Суммой 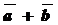 векторов
векторов 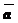 и
и 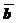 называется композиция этих векторов.
называется композиция этих векторов.
Рис. 1. Рис. 2.
«Правило треугольника»: Чтобы сложить 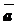 и
и 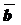 по «правилу треугольника», надо от произвольной точки плоскости отложить
по «правилу треугольника», надо от произвольной точки плоскости отложить  , от конца
, от конца 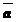 отложить
отложить 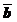 . Суммой векторов
. Суммой векторов  и
и 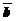 будет вектор
будет вектор 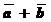 , начало которого совпадет с началом
, начало которого совпадет с началом  , конец - с концом
, конец - с концом 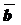 . (Рис. 1.)
. (Рис. 1.)
«Правило параллелограмма»: Чтобы сложить 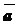 и
и 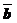 по «правилу параллелограмма», надо от произвольной точки на плоскости отложить
по «правилу параллелограмма», надо от произвольной точки на плоскости отложить  и
и 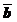 и на них, как на сторонах, построить параллелограмм. Суммой векторов
и на них, как на сторонах, построить параллелограмм. Суммой векторов  и
и 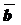 будет вектор
будет вектор 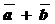 , изображаемый диагональю параллелограмма, идущей из их общего начала. (Рис. 2.)
, изображаемый диагональю параллелограмма, идущей из их общего начала. (Рис. 2.)
При сложении нескольких векторов пользуются правилом многоугольника.
«Правило многоугольника»:
Чтобы сложить несколько векторов по «правилу многоугольника», надо отложить от произвольной точки плоскости первый вектор, от конца первого вектора отложить второй вектор, от конца второго – третий и т.д. Вектором суммы будет вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего вектора.
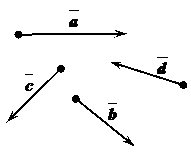 Пример:
Пример:
Дано: 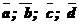
 Построить:
Построить: 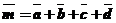
Вычитание векторов
Определение: Разностью 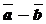 двух векторов
двух векторов 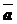 и
и 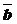 называется сумма вектора
называется сумма вектора 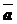 и вектора, противоположного вектору
и вектора, противоположного вектору 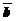 .
.
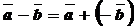
Правило: Разностью двух векторов является вектор, начало которого совпадает с концом вектора – вычитаемого, а конец – с концом вектора –уменьшаемого, если они отложены от одной точки.
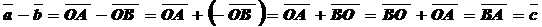
Умножение вектора на число
Определение: Произведением ненулевого вектора 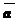 на число х, неравное нулю, называется вектор
на число х, неравное нулю, называется вектор 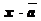 , длина которого равна
, длина которого равна 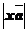 , а направление совпадает с направлением
, а направление совпадает с направлением  , если х > 0, и противоположно ему, если
, если х > 0, и противоположно ему, если
х < 0.
Замечание: Произведение нулевого вектора на любое число и произведение любого вектора на нуль по определению считается равным нулевому вектору.
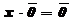 ;
; 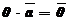 .
. 
Пример: Дано: 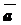 ; х1 = - 2; х2 = 3; х3 =
; х1 = - 2; х2 = 3; х3 = 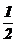 .
.
Построить: - 2 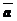 ; 3
; 3 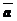 ;
; 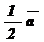 .
.
Упражнения:
1. По данным векторам 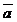 и
и 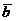 построить следующие векторы:
построить следующие векторы:
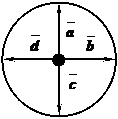

2. Найти сумму изображенных на рисунке векторов.
3. По данным векторам 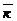 ,
, 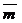 и
и 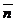 построить следующие векторы:
построить следующие векторы: 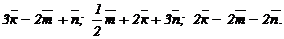
- Декартова система координат на плоскости





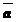 и
и 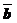 противоположные векторы, то пишут
противоположные векторы, то пишут 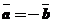 или
или 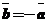 .
.
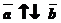
 и
и 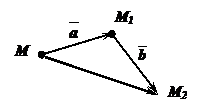 Сложение векторов.
Сложение векторов.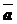 и
и 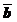 .
.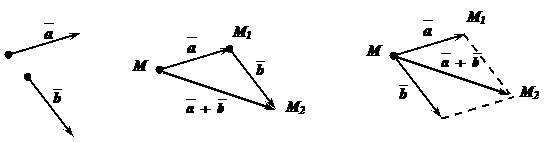 Определение: Суммой
Определение: Суммой 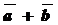 векторов
векторов 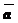 и
и 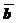 называется композиция этих векторов.
называется композиция этих векторов.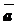 и
и 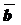 по «правилу треугольника», надо от произвольной точки плоскости отложить
по «правилу треугольника», надо от произвольной точки плоскости отложить 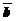 будет вектор
будет вектор 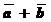 , начало которого совпадет с началом
, начало которого совпадет с началом 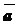 и
и 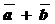 , изображаемый диагональю параллелограмма, идущей из их общего начала. (Рис. 2.)
, изображаемый диагональю параллелограмма, идущей из их общего начала. (Рис. 2.)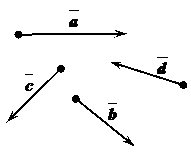 Пример:
Пример: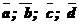
 Построить:
Построить: 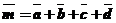
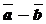 двух векторов
двух векторов 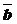 называется сумма вектора
называется сумма вектора 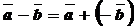
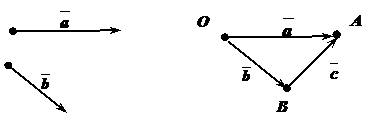
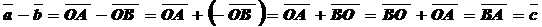
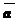 на число х, неравное нулю, называется вектор
на число х, неравное нулю, называется вектор 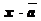 , длина которого равна
, длина которого равна 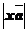 , а направление совпадает с направлением
, а направление совпадает с направлением 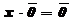 ;
; 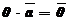 .
. 
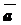 ; х1 = - 2; х2 = 3; х3 =
; х1 = - 2; х2 = 3; х3 = 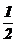 .
.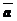 ; 3
; 3 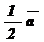 .
.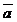 и
и 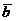 построить следующие векторы:
построить следующие векторы: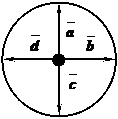

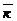 ,
, 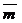 и
и 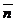 построить следующие векторы:
построить следующие векторы: