Определение: Базисом пространства называются три некомпланарных вектора, взятых в определенном порядке.
 - базис пространства.
- базис пространства.
 Определение: Декартовой системой координат в пространстве называется множество, состоящее из точки О и базиса пространства.
Определение: Декартовой системой координат в пространстве называется множество, состоящее из точки О и базиса пространства.
 - декартова система координат в пространстве.
- декартова система координат в пространстве.
О – начало координат;
Ох – ось абсцисс;
Оу – ось ординат;
Оz – ось аппликат.
Замечание: Любой вектор  может быть единственным образом разложен по базисным векторам
может быть единственным образом разложен по базисным векторам  :
:  . Числа х, у, z называются координатами вектора
. Числа х, у, z называются координатами вектора  в данной декартовой системе координат.
в данной декартовой системе координат.
 Определение: Декартова система координат в пространстве называется прямоугольной, если базисные векторы попарно взаимно перпендикулярны и единичны.
Определение: Декартова система координат в пространстве называется прямоугольной, если базисные векторы попарно взаимно перпендикулярны и единичны.
 – прямоугольная декартова система координат в пространстве.
– прямоугольная декартова система координат в пространстве.
 .
.
О – начало координат;
Ох – ось абсцисс;
Оу – ось ординат;
Оz – ось аппликат.
Замечание: 1. Базисные векторы  в прямоугольной декартовой системе координат называются ортами.
в прямоугольной декартовой системе координат называются ортами.
 2. Любой вектор
2. Любой вектор  может быть единственным образом разложен по ортам
может быть единственным образом разложен по ортам  :
:  . Числа х, у, z являются координатами вектора
. Числа х, у, z являются координатами вектора  в данной прямоугольной декартовой системе координат.
в данной прямоугольной декартовой системе координат.
Пример:
Дано: ABCDA1B1C1D1 – куб.
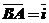 ;
;  ;
;  .
.
M – середина AD;
H – середина DC;
F – середина AA1;
N – середина A1 B1;
K – середина B1 C1;
L – середина D1 C1;
P – середина C1 C.
Разложить векторы  по векторам
по векторам  .
.
Решение:
Воспользуемся «правилом многоугольника» сложения нескольких векторов:
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Упражнения:
1. Дан куб ABCDA1B1C1D1. Являются ли компланарными следующие векторы:
а)  г)
г) 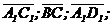
б)  д)
д) 
в)  е)
е) 
2. В кубе ABCDA1B1C1D1 за базис взяты векторы  ;
; 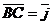 ;
;  ;
;
M – середина A1 B1; N – середина B1 C1; S – середина BC; Q – середина AD;
R – середина CD; T – середина BB1; P – середина AB. Разложить по базису  векторы
векторы  .
.
5. Построение точек плоскости (пространства), заданных координатами
Пример:
Построить в 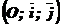 точки
точки
А(2; - 3);
В (- 1; 4);
С (- 3; - 2);
D(0; - 1).
 Пример: Построить в
Пример: Построить в  точки
точки
А(2; 3; 4);
В (- 1; - 3; 3);
С (0; 4; 2);
D(0; 0; 5);
Е(- 2; 0; 6).
6. Понятие радиус-вектора точки. Разложение радиус-вектора точки по ортам
Определение; Радиус-вектором точки называется вектор, начало которого совпадает с началом координат, а конец с данной точкой.
Вывод:
1. Каждой точке плоскости (пространства) соответствует свой радиус-вектор.
Координаты радиус-вектора точки совпадают с координатами самой точки.
Сумма произведений координат радиус-вектора точки М на соответствующие орты называется разложением радиус-вектора точки М по ортам.
Рис. 1. Рис. 2.
Рис. 1.
В  точка М (х; у) имеет радиус-вектор
точка М (х; у) имеет радиус-вектор  .
.
Рис. 2.
В  точка М (х; у; z) имеет радиус-вектор
точка М (х; у; z) имеет радиус-вектор  .
.
Упражнения:
1. Определить координаты орт в  и
и  .
.
2. Построить радиус-векторы точек А (2; - 1; 4); В (- 3; 2; - 5); С (0; 0; 4).
3. Разложить радиус-векторы точек А (- 1; 4; 0); В (2; - 2; 5); С (0; 3; - 2) по ортам.
4. Определить координаты радиус-векторов точек М, К, L, E, H если:
 .
.
7. Определение координат вектора на плоскости и в пространстве
Задача: Определить координаты 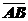 в
в  ,
,
если А (х1; у1) и В (х2; у2).
Дано:
 ;
;
А (х1; у1);
В (х2; у2).
Определить:
 .
.
Решение:
Построим радиус-векторы 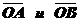 точек А и В.
точек А и В.
А (х1; у1)  - разложение
- разложение 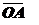 по ортам;
по ортам;
В (х2; у2)  - разложение
- разложение  по ортам;
по ортам;
По правилу вычитания двух векторов 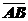 можно представить в виде разности
можно представить в виде разности 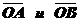 .
.

 - разложение
- разложение 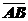 по ортам, где х = х2 - х1; у = у2 - у1.
по ортам, где х = х2 - х1; у = у2 - у1.

Вывод: Разложить вектор по ортам, значит представить его в виде суммы произведений координат вектора на соответствующие орты.

 .
. 
 .
.
Правило: Чтобы определить координаты любого вектора, надо из координат конца этого вектора вычесть одноименные координаты его начала.
 .
.
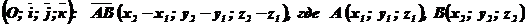 .
.
Пример: Определить координаты 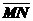 , если М (- 3; 0; 4) и N (1; - 5; - 3).
, если М (- 3; 0; 4) и N (1; - 5; - 3).
 Дано: Решение:
Дано: Решение:
 Воспользуемся правилом определения координат вектора:
Воспользуемся правилом определения координат вектора:






 - базис пространства.
- базис пространства. Определение: Декартовой системой координат в пространстве называется множество, состоящее из точки О и базиса пространства.
Определение: Декартовой системой координат в пространстве называется множество, состоящее из точки О и базиса пространства. - декартова система координат в пространстве.
- декартова система координат в пространстве. может быть единственным образом разложен по базисным векторам
может быть единственным образом разложен по базисным векторам  :
:  . Числа х, у, z называются координатами вектора
. Числа х, у, z называются координатами вектора  Определение: Декартова система координат в пространстве называется прямоугольной, если базисные векторы попарно взаимно перпендикулярны и единичны.
Определение: Декартова система координат в пространстве называется прямоугольной, если базисные векторы попарно взаимно перпендикулярны и единичны. – прямоугольная декартова система координат в пространстве.
– прямоугольная декартова система координат в пространстве. .
. в прямоугольной декартовой системе координат называются ортами.
в прямоугольной декартовой системе координат называются ортами. 2. Любой вектор
2. Любой вектор  :
:  . Числа х, у, z являются координатами вектора
. Числа х, у, z являются координатами вектора 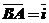 ;
;  ;
;  .
. по векторам
по векторам  ;
; ;
; ;
; ;
; .
. г)
г) 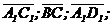
 д)
д) 
 е)
е) 
 ;
; 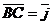 ;
;  ;
; векторы
векторы  .
.
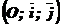 точки
точки Пример: Построить в
Пример: Построить в  точки
точки
 точка М (х; у) имеет радиус-вектор
точка М (х; у) имеет радиус-вектор  .
. .
. и
и  .
. .
.
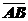 в
в  .
.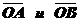 точек А и В.
точек А и В. - разложение
- разложение 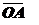 по ортам;
по ортам; - разложение
- разложение  по ортам;
по ортам;
 - разложение
- разложение 
 .
.  .
. .
.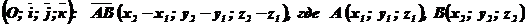 .
.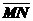 , если М (- 3; 0; 4) и N (1; - 5; - 3).
, если М (- 3; 0; 4) и N (1; - 5; - 3). Дано: Решение:
Дано: Решение:


