

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
Топ:
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Определение: Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными.
Замечание: Нулевой вектор считается коллинеарным любому вектору.
 |
 Þ
Þ 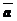 и
и 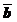 коллинеарные
коллинеарные 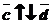 Þ
Þ  и
и  коллинеарные
коллинеарные
Векторы векторы
Вывод: Коллинеарные векторы лежат на одной прямой или на параллельных прямых.
Необходимый и достаточный признак коллинеарности двух векторов.
Теорема: Для того, чтобы вектор 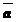 был коллинеарен ненулевому вектору
был коллинеарен ненулевому вектору 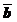 , необходимо и достаточно, чтобы существовало число к, удовлетворяющее условию
, необходимо и достаточно, чтобы существовало число к, удовлетворяющее условию  .
.
Разложение вектора на плоскости по двум неколлинеарным векторам
Теорема: Любой вектор 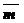 может быть представлен и, притом, единственным образом, в виде линейной комбинации двух любых неколлинеарных векторов
может быть представлен и, притом, единственным образом, в виде линейной комбинации двух любых неколлинеарных векторов 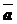 и
и 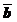 .
.
Дано: 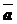 и
и 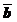 неколлинеарны;
неколлинеарны;
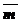 - произвольный вектор плоскости.
- произвольный вектор плоскости.
Доказать:
1.  существует;
существует;
2.  единственным образом .
единственным образом .
Доказательство:
1. Докажем, что разложение  существует.
существует.
 Пусть
Пусть  и
и 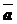 коллинеарны, следовательно, по признаку коллинеарности двух векторов
коллинеарны, следовательно, по признаку коллинеарности двух векторов  . Значит, верно равенство
. Значит, верно равенство  .
.
Пусть  и
и 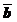 коллинеарны, следовательно, по признаку коллинеарности двух векторов
коллинеарны, следовательно, по признаку коллинеарности двух векторов  . Значит, верно равенство
. Значит, верно равенство  .
.

Пусть  неколлинеарен векторам
неколлинеарен векторам 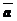 и
и  (
( ;
;  ).
).
Через конец вектора  проведем прямые, параллельные векторам
проведем прямые, параллельные векторам 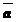 и
и 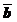 . Прямые, которым принадлежат векторы
. Прямые, которым принадлежат векторы 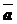 и
и 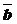 , продолжим до пересечения с построенными прямыми, достраивая параллелограмм ОАМВ.
, продолжим до пересечения с построенными прямыми, достраивая параллелограмм ОАМВ.
 ;
;
 и
и  коллинеарны, следовательно, по признаку коллинеарности двух векторов
коллинеарны, следовательно, по признаку коллинеарности двух векторов  .
.
 и
и 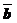 коллинеарны, следовательно, по признаку коллинеарности двух векторов
коллинеарны, следовательно, по признаку коллинеарности двух векторов  .
.
 ;
;  , что и требовалось доказать.
, что и требовалось доказать.
2. Единственность разложения  доказывается методом от противного.
доказывается методом от противного.
Замечание: Если  , то говорят, что вектор
, то говорят, что вектор 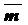 разложен по векторам
разложен по векторам 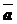 и
и 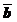 .
.
Базис плоскости. Декартова система координат на плоскости.
Прямоугольная декартова система координат на плоскости
 |
Определение: Базисом плоскости называется пара неколлинеарных векторов этой плоскости, взятых в определенном порядке.
 – базис плоскости, где
– базис плоскости, где  .
.
Определение: Декартовой системой координат на плоскости называется множество, состоящее из точки О и базиса плоскости.
 – декартова система координат на плоскости.
– декартова система координат на плоскости.

О – начало координат;
О х – ось абсцисс;
О у – ось ординат.
Замечание: Любой вектор 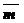 может быть единственным образом разложен по базисным векторам
может быть единственным образом разложен по базисным векторам  и
и  :
: 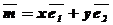 . Числа х и у называются координатами вектора
. Числа х и у называются координатами вектора 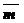 в данной декартовой системе координат.
в данной декартовой системе координат.
 Определение: Декартова система координат на плоскости называется прямоугольной, если базисные векторы взаимно перпендикулярны и единичны.
Определение: Декартова система координат на плоскости называется прямоугольной, если базисные векторы взаимно перпендикулярны и единичны.
|
|
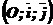 – прямоугольная декартова система координат на плоскости.
– прямоугольная декартова система координат на плоскости.
 .
.
О – начало координат;
Ох – ось абсцисс;
Оу – ось ординат.
Замечание:
1. Базисные векторы  в прямоугольной декартовой системе координат называются ортами.
в прямоугольной декартовой системе координат называются ортами.
2. Любой вектор 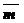 может быть единственным образом разложен по ортам
может быть единственным образом разложен по ортам  :
:  . Числа х и у являются координатами вектора
. Числа х и у являются координатами вектора 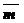 в данной прямоугольной декартовой системе координат.
в данной прямоугольной декартовой системе координат.
Упражнения:
1. Доказать, что  и
и  коллинеарны.
коллинеарны.
 2. В прямоугольнике АВСD проведены диагонали АС и ВD, пересекающиеся в точке О.
2. В прямоугольнике АВСD проведены диагонали АС и ВD, пересекающиеся в точке О. 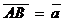 ,
,  . Выразить через
. Выразить через 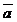 и
и 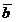 следующие векторы:
следующие векторы: 
4. Декартова система координат в пространстве
4. 1. Понятие компланарных векторов
Определение: Ненулевые вектора называются компланарными, если они параллельны одной и той же плоскости.
Замечание: Любые два вектора всегда компланарны, а три вектора могут и не быть компланарными.
Векторы  компланарны, а векторы
компланарны, а векторы  компланарными не являются.
компланарными не являются.
4. 2. Разложение вектора в пространстве по трем некомпланарным векторам
Теорема: Если даны три некомпланарных вектора 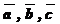 , то любой вектор
, то любой вектор  можно разложить по векторам
можно разложить по векторам 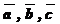 единственным образом.
единственным образом.
 |
Дано: 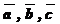 - некомпланарные векторы;
- некомпланарные векторы;
 - произвольный вектор пространства.
- произвольный вектор пространства.
Доказать: 1. 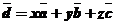 - существует;
- существует;
2. 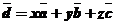 - единственное.
- единственное.
|
|
|

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!