1. Любая линейная комбинация собственных векторов, отвечающих одному и тому же собственному числу, является также собственным вектором с тем же собственным числом.
2. Если собственные векторы  отвечают попарно различным собственным числам λ1, λ2, …, λk, то система векторов
отвечают попарно различным собственным числам λ1, λ2, …, λk, то система векторов  линейно независима.
линейно независима.
3. Собственные числа линейного оператора А: V → W не изменяются при изменении базиса.
Пример:
Найти собственные значения и собственные векторы для матрицы

Решение: составим характеристическое уравнение
 .
.
Вычисляя этот определитель, получим (λ + 1)2(λ – 3) = 0, λ1 = –1, λ2 = 3.
Система для определения собственного вектора, соответствующего собственному значению λ2 = 3 имеет вид:

Третье уравнение равно разности второго и первого, поэтому его можно вычеркнуть из системы. Получим систему 
В качестве свободной неизвестной величины можно выбрать х3 и выразить через неё неизвестные х 1 и х 2. Получим

Полагая х 3 = 2, найдем собственный вектор 
Аналогично найдём собственный вектор, соответствующий собственному числу λ1 = –1, 
Заметим, что собственному числу λ1 = –1 кратности 2 соответствует лишь один с точностью до постоянного множителя собственный вектор, так как в рассматриваемом примере rang(A – λT) = 2 при λ = –1. Таким образом, матрица А имеет лишь два линейно независимых собственных вектора.
Задания для самостоятельной работы
1. Найти длину и направляющие косинусы вектора:
1.1.  . 1.2.
. 1.2.  .
.
2. Найти орт вектора:
2.1.  . 2.2.
. 2.2.  . 2.3.
. 2.3.  .
.
3. Образуют ли трапецию точки А (3;–1;2), В(1;2; –1), С(–1;1; –3), D (3; –5;3)?
4. Точки А, В, С, D – вершины параллелограмма. Точка О – точка пересечения его диагоналей (его центр). Найти разложение векторов  по векторам
по векторам  .
.
5. Вычислить скалярное произведение векторов:
5.1.  и
и  . 5.2.
. 5.2.  и
и  . 5.3.
. 5.3.  и
и  .
.
6. Найти пр  и пр
и пр  :
:
6.1.  ,
,  . 6.2.
. 6.2.  ,
,  . 6.3.
. 6.3.  ,
,  .
.
7. Вычислить векторное произведение векторов:
7.1.  и
и  . 7.2.
. 7.2. 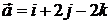 ,
, 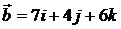 . 7.3.
. 7.3.  ,
,  .
.
8. Найти синус угла между векторами:
8.1.  и
и  . 8.2.
. 8.2.  и
и  . 8.3.
. 8.3.  и
и  .
.
9. Указать левой или правой тройкой являются векторы  :
:
9.1.  ,
,  ,
,  . 9.2.
. 9.2.  ,
,  ,
,  . 9.3.
. 9.3.  ,
,  ,
,  .
.
10. Компланарны ли векторы:
10.1.  ,
,  ,
,  . 10.2.
. 10.2.  ,
,  ,
,  .
.
11. Найти объём тетраэдра построенного на векторах  :
:
11.1.  ,
,  ,
,  . 11.2.
. 11.2.  ,
,  ,
,  .
.
12. Найти собственные числа и собственные векторы линейного оператора, заданного матрицей

13. Показать, что собственные векторы матрицы  ортогональны.
ортогональны.
Ответы
1.1. 1,66; 0,12; 0,24; 0,96. 1.2. 70; 2/7;3/7;-6/7. 2.1. 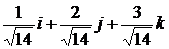 . 2.2.
. 2.2.  . 2.3. 0,27 i +0,53 j +0,80 k. 3. Да. 4.
. 2.3. 0,27 i +0,53 j +0,80 k. 3. Да. 4.  ;
;  ;
;  ;
;  . 5.1. –5. 5.2. 10. 5.3. 0. 6.1. пр
. 5.1. –5. 5.2. 10. 5.3. 0. 6.1. пр  , пр
, пр  . 6.2. пр
. 6.2. пр  , пр
, пр  . 6.3. пр
. 6.3. пр  , пр
, пр 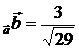 . 7.1. 6 i – 3j. 7.2. 20 i – 20 j – 10 k. 7.3. (3;4;-2). 8.1. 1. 13.2. (167/185)1/2. 8.3. (5/56)1/2. 9.1. Левая. 9.2. Правая. 9.3. Левая. 10.1. Нет. 10.2. Да. 11.1. 24 куб.ед. 11.2. 2 куб.ед. 12. λ1 = 1, λ2 = 2, λ3= 3.
. 7.1. 6 i – 3j. 7.2. 20 i – 20 j – 10 k. 7.3. (3;4;-2). 8.1. 1. 13.2. (167/185)1/2. 8.3. (5/56)1/2. 9.1. Левая. 9.2. Правая. 9.3. Левая. 10.1. Нет. 10.2. Да. 11.1. 24 куб.ед. 11.2. 2 куб.ед. 12. λ1 = 1, λ2 = 2, λ3= 3.  ,
, 
 13. λ1 = 9, λ2= 6, λ3 = 3.
13. λ1 = 9, λ2= 6, λ3 = 3.
Вопросы для самоподготовки
1. Векторы.
2. Линейные операции над векторами и их свойства.
3. Линейные пространства. Типы линейных пространств.
4. Чему равна проекция вектора на ось?
5. Координаты вектора в декартовой прямоугольной системе координат. Длина вектора.
6. Коллинеарные векторы. Условие коллинеарности векторов.
7. Скалярное произведение векторов, его свойства.
8. Угол между векторами. Условие перпендикулярности двух векторов.
9. Скалярное произведение векторов в координатной форме.
10. Геометрический и физический смысл скалярного произведения.
11. Евклидово пространство. Норма вектора.
12. Векторное произведение двух векторов.
13. Векторное произведение векторов в координатной форме.
14. Геометрический, физический и механический смысл векторного произведения.
15. Смешанное произведение трех векторов.
16. Смешанное произведение в координатной форме.
17. Геометрический смысл смешанного произведения.
18. Евклидово пространство. Неравенство Коши-Буняковского
19. Определение Линейного оператора.
20. Действия над линейными операторами.
21. Обратный оператор.
22. Собственные векторы и собственные числа.
23. Свойства собственных векторов.



 отвечают попарно различным собственным числам λ1, λ2, …, λk, то система векторов
отвечают попарно различным собственным числам λ1, λ2, …, λk, то система векторов 
 .
.




 . 1.2.
. 1.2.  .
. . 2.2.
. 2.2.  . 2.3.
. 2.3.  .
. по векторам
по векторам  .
. и
и  . 5.2.
. 5.2.  и
и  . 5.3.
. 5.3.  и
и  .
. и пр
и пр  :
: ,
,  . 6.2.
. 6.2.  ,
,  . 6.3.
. 6.3.  ,
,  .
. . 7.2.
. 7.2. 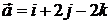 ,
, 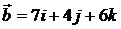 . 7.3.
. 7.3.  ,
,  .
. и
и  . 8.2.
. 8.2.  и
и  . 8.3.
. 8.3.  и
и  .
. :
: ,
,  ,
,  . 9.2.
. 9.2.  ,
,  ,
,  . 9.3.
. 9.3.  ,
,  ,
,  .
. ,
,  ,
,  . 10.2.
. 10.2.  ,
,  ,
,  .
. :
: ,
,  ,
,  . 11.2.
. 11.2.  ,
,  ,
,  .
.
 ортогональны.
ортогональны.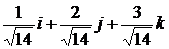 . 2.2.
. 2.2.  . 2.3. 0,27 i +0,53 j +0,80 k. 3. Да. 4.
. 2.3. 0,27 i +0,53 j +0,80 k. 3. Да. 4.  ;
;  ;
;  ;
;  . 5.1. –5. 5.2. 10. 5.3. 0. 6.1. пр
. 5.1. –5. 5.2. 10. 5.3. 0. 6.1. пр  , пр
, пр  . 6.2. пр
. 6.2. пр  , пр
, пр  . 6.3. пр
. 6.3. пр  , пр
, пр 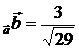 . 7.1. 6 i – 3j. 7.2. 20 i – 20 j – 10 k. 7.3. (3;4;-2). 8.1. 1. 13.2. (167/185)1/2. 8.3. (5/56)1/2. 9.1. Левая. 9.2. Правая. 9.3. Левая. 10.1. Нет. 10.2. Да. 11.1. 24 куб.ед. 11.2. 2 куб.ед. 12. λ1 = 1, λ2 = 2, λ3= 3.
. 7.1. 6 i – 3j. 7.2. 20 i – 20 j – 10 k. 7.3. (3;4;-2). 8.1. 1. 13.2. (167/185)1/2. 8.3. (5/56)1/2. 9.1. Левая. 9.2. Правая. 9.3. Левая. 10.1. Нет. 10.2. Да. 11.1. 24 куб.ед. 11.2. 2 куб.ед. 12. λ1 = 1, λ2 = 2, λ3= 3.  ,
, 
 13. λ1 = 9, λ2= 6, λ3 = 3.
13. λ1 = 9, λ2= 6, λ3 = 3.


