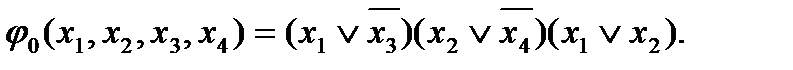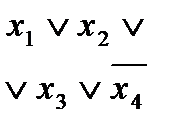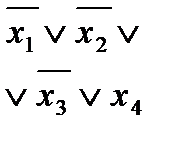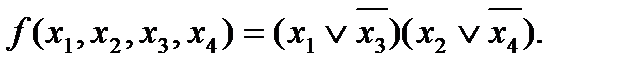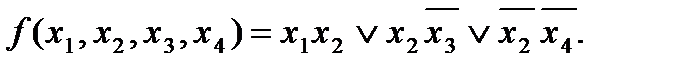В ЦВМ могут использоваться комбинационные схемы, закон функционирования которых определен неполностью. В таких схемах некоторые комбинации сигналов на ее входы не подаются и являются запрещенными. Для запрещенных входных комбинаций выходные сигналы не определены, т.е. могут принимать любые значения – нуль или единицу. Поэтому при синтезе схем с неполностью заданным законом функционирования можно произвольно задать значения выходных сигналов для запрещенных комбинаций входных сигналов; нормальная работа схемы при этом не нарушается. Поэтому выходным сигналам на запрещенных комбинациях придают такие значения, при которых можно построить наиболее простую схему.
Схемы с запрещенными комбинациями выходных сигналов описываются неполностью определенными переключательными функциями, т.е. функциями, значения которых определены не на всех наборах. Например, функция, заданная таблицей истинности и диаграммой Вейча,
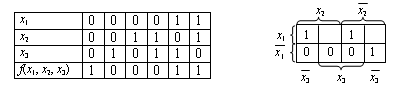
определена только на шести наборах. Клетки, соответствующие наборам 1,0,0; 1,1,1, остаются пустыми.
Форма представления функции f (x 1, x 2, x 3) существенно зависит от выбора ее значений на запрещенных наборах, Например, для заданной функции, выбирая ее запрещенные значения равными нулю, можно получить минимальную ДНФ в виде

Если значения функции на запрещенных наборах принять равными единице, то форма представления упрощается:
 .
.
Рассмотрим общую методику получения минимальных ДНФ неполностью определенных переключательных функций
Определение 2.3. Пусть переключательная функция f(x1, x2, …, xn) не определена на p наборах аргументов. Тогда полностью определенную функцию j(x1, x2, …, xn) будем называть эквивалентной функции f(x1, x2, …, xn), если ее значения совпадают со значениями функции f(x1, x2, …, xn) на тех наборах, на которых функция f определена.
Существует 2 p вариантов выбора значений функции на запрещенных наборах и, следовательно, 2 р различных переключательных функций, эквивалентных функции f (x 1, x 2, …, xn). Поэтому задача минимизации неполностью определенной функции f (x 1, x 2, …, xn) сводится к отысканию такой эквивалентной функции j (x 1, x 2, …, xn), которая имеет простейшую минимальную форму.
Введем эквивалентные функции j 0(x 1, x 2, …, xn) и j 1(x 1, x 2, …, xn), значения которых на всех запрещенных наборах функции f (x 1, x 2, …, xn) равны соответственно нулю и единице.
Теорема 2.3. Минимальная ДНФ неполностью определенной функции f(x1, x2, …, xn) совпадает с дизъюнкцией самых коротких импликант эквивалентной функции j1(x1, x2, …, xn), которые совместно поглощают все конституенты единицы функции j0(x1, x2, …, xn) и ни одна из которых не является лишней.
Для доказательства теоремы рассмотрим СДНФ некоторой эквивалентной функции ji (x 1, x 2, …, xn). Конституенты единицы, входящие в эту форму, обязательно войдут и в СДНФ функции j 1(x 1, x 2, …, xn). Поэтому любая простая импликанта функции ji (x 1, x 2, …, xn) будет совпадать с импликантой функции j 1(x 1, x 2, …, xn) или будет поглощаться ею. Другими словами, среди импликант функции j 1(x 1, x 2, …, xn) всегда найдется такая, которая поглощает любую импликанту любой эквивалентной функции ji (x 1, x 2, …, xn). Следовательно, самыми короткими произведениями, накрывающими единицы функции f (x 1, x 2, …, xn), будут импликанты j 1(x 1, x 2, …, xn).
Среди всех ПФ, эквивалентных заданной, функция j 0(x 1, x 2, …, xn) имеет минимальное количество конституент единицы. Следовательно, и количество простых импликант [из набора импликант функции j 1(x 1, x 2, …, xn)], необходимых для поглощения конституент функции j 0(x 1, x 2, …, xn), будет минимальным. Если составить дизъюнкции наиболее коротких импликант функции j 0(x 1, x 2, …, xn), которые совместно накрывают все конституенты единицы функции j 0(x 1, x 2, …, xn), то получим, очевидно, минимальную форму представления функции f (x 1, x 2, …, xn).
Ввиду того, что для накрытия единиц функции j 0(x 1, x 2, …, xn) выбираются импликанты другой функции, дизъюнкция этих импликант не равняется функции j 0(x 1, x 2, …, xn). Однако такая дизъюнкция обязательно равна одной из функций, эквивалентных функции f (x 1, x 2, …, xn).
Пример 2.11. Найти минимальную дизъюнктивную нормальную форму ПФ, заданной таблицей истинности (табл. 2.6).
Таблица 2.6
Таблица истинности неполностью определенной функции
| x 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x 4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| f (x 1, x 2, x 3, x 4)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагая, что пустые клетки заполнены нулями, найдем СДНФ эквивалентной функции j 0(x 1, x 2, x 3, x 4):
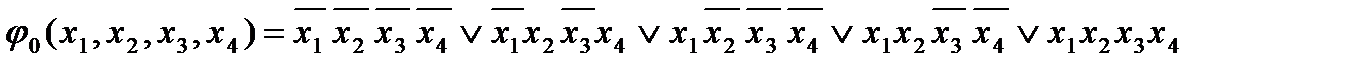 .
.
СНДФ функции j 1(x 1, x 2, …, xn), полученная после заполнения пустых клеток таблицы единицами, будет такой:

Выполнив операции неполного склеивания и поглощения, получим сокращенную ДНФ функции j 1(x 1, x 2, x 3, x 4), в которую войдут все ее простые импликанты:
 .
.
Составим импликантную матрицу, включив в нее конституенты единицы функции j 0(x 1, x 2, x 3, x 4) и импликанты функции j 1(x 1, x 2, x 3, x 4) (табл. 2.7).
Таблица 2.7
Импликантная матрица
| Импликанты
| Конституенты
|
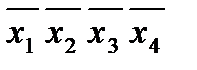
| 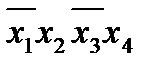
| 
| 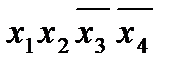
| x 1 x 2 x 3 x 4
|
| x 1 x 2
|
|
|
| x
| x
|

| x
|
|
|
|
|

|
|
| x
| x
|
|

| x
|
| x
|
|
|

|
| x
|
|
|
|

|
| x
|
|
|
|
Импликанта x 1 x 2 обязательно должна входить в минимальную ДНФ, так как только она поглощает конституенту x 1 x 2 x 3 x 4. Импликанты x 1 x 2 и  совместно накрывают все конституенты, кроме
совместно накрывают все конституенты, кроме  ; последняя может быть накрыта импликантами
; последняя может быть накрыта импликантами 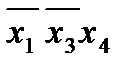 или
или  . Поэтому минимальные ДНФ функции f (x 1, x 2, x 3, x 4) будут:
. Поэтому минимальные ДНФ функции f (x 1, x 2, x 3, x 4) будут:


Пример 2.12. Найти минимальную ДНФ функции f (x 1, x 2, x 3, x 4), эквивалентная функция j 0(x 1, x 2, x 3, x 4) которой имеет вид

а комбинации  являются запрещенными.
являются запрещенными.
Эквивалентную функцию j 1(x 1, x 2, …, xn) можно получить, добавив к СДНФ функции j 1(x 1, x 2, …, xn) запрещенные комбинации переменных:

Проведя операции неполного склеивания и поглощения, найдем простые импликанты функции j 1(x 1, x 2, x 3, x 4): x 1 x 2 x 3, x 1 x 3 x 4,  ,
,  . Импликантная матрица функции f (x 1, x 2, x 3, x 4) имеет вид (табл. 2.8).
. Импликантная матрица функции f (x 1, x 2, x 3, x 4) имеет вид (табл. 2.8).
Таблица 2.8
Импликантная матрица
| Импликанты
| Конституенты
|

| 
| 
| 
| 
|

|
|
|
| x
| x
|

|
| х
| х
|
| х
|
| x1x2x3
| х
|
|
|
|
|
| x1x3x4
|
|
|
|
|
|
Функция f (x 1, x 2, x 3, x 4) имеет единственную минимальную ДНФ:

В нижней строке импликантной матрицы крестики отсутствуют и, следовательно, импликанта x 1 x 3 x 4 не поглощает ни одну из конституент единицы функции j 0(x 1, x 2, x 3, x 4). Это связано с тем, что данная импликанта образовалась в результате склеивания конституент функции j 1(x 1, x 2, x 3, x 4), которые в функцию j 0(x 1, x 2, x 3, x 4) не входят.
Чтобы найти простейшее представление неполностью определенной ПФ, кроме минимальных дизъюнктивных форм следует получить минимальные конъюнктивные нормальные формы и выбрать ту из них, которая содержит наименьшее число букв.
Алгоритм получения минимальных конъюнктивных форм подобен рассмотренному алгоритму получения минимальной ДНФ и заключается в следующем.
Пусть задана неполностью определенная функция f (x 1, x 2, …, xn). Тогда для получения минимальной КНФ достаточно найти сокращенную КНФ эквивалентной функции j 0(x 1, x 2, …, xn), а функцию j 1(x 1, x 2, …, xn) записать в СКНФ. Затем следует составить ипликантную матрицу, включив в нее все конституенты нуля функции j 1(x 1, x 2, …, xn) и все члены сокращенной конъюнктивной нормальной формы функции j 0(x 1, x 2, …, xn). По импликантной матрице рассмотренным выше способом можно получить минимальные КНФ функции f (x 1, x 2, …, xn).
Пример 2.13. Найти минимальную КНФ функции, заданной таблицей (табл. 2.9).
Таблица 2.9
Таблица истинности неполностью определенной ПФ
| x 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x 4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| f (x 1, x 2, x 3, x 4)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СКНФ эквивалентной функции j1(x 1, x 2, x 3, x 4):


СКНФ функции 


Сокращенная КНФ функции j 0(x 1, x 2, x 3, x 4):
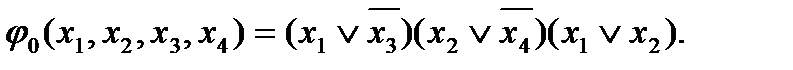
Импликантная матрица имеет вид (табл. 2.10).
Таблица 2.10
Импликантная матрица
| Импли-
канты
| 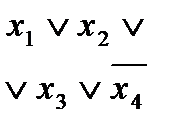
| 
| 
| 
| 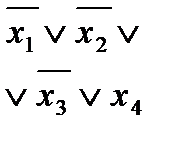
|
|
|
|
|
|
|

| х
| х
| х
|
|
|

| х
|
|
| х
| х
|

| х
|
|
|
|
|
Минимальная КНФ функции f (x 1, x 2, x 3, x 4):
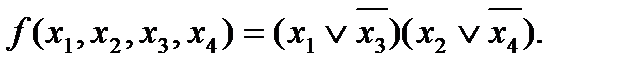
Рассмотренная функция имеет четыре минимальные ДНФ:

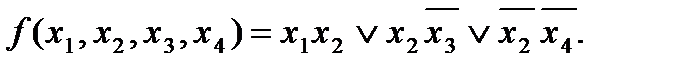


В этих формах больше букв, чем в минимальной КНФ.
ПРАКТИЧЕСКИЙ РАЗДЕЛ





 .
.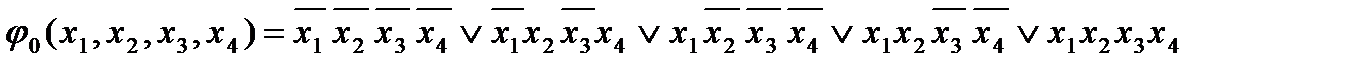 .
.
 .
.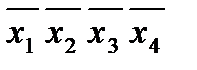
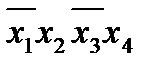

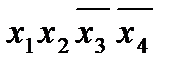





 совместно накрывают все конституенты, кроме
совместно накрывают все конституенты, кроме  ; последняя может быть накрыта импликантами
; последняя может быть накрыта импликантами 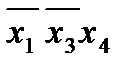 или
или  . Поэтому минимальные ДНФ функции f (x 1, x 2, x 3, x 4) будут:
. Поэтому минимальные ДНФ функции f (x 1, x 2, x 3, x 4) будут:


 являются запрещенными.
являются запрещенными.
 ,
,  . Импликантная матрица функции f (x 1, x 2, x 3, x 4) имеет вид (табл. 2.8).
. Импликантная матрица функции f (x 1, x 2, x 3, x 4) имеет вид (табл. 2.8).