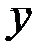Существует шестнадцать различных переключательных функций двух аргументов, каждая из которых определена на четырех наборах. Эти функции представлены в табл. 1.4.
В число шестнадцати переключательных функций входят функции, рассмотренные в п.1.2.1:
f0(x,y) = 0 — константа нуль;
f15(x,y) = 1 — константа единица;
f3(x,y) = x — переменная x;
f5(x,y) = y — переменная y;
f12(x,y) =  — инверсия x;
— инверсия x;
f10(x,y) =  — инверсия y;
— инверсия y;
Таблица 1.4
Переключательные функции двух аргументов
| x
|
|
|
|
| Название функции
| Обозначение
|
| y
|
|
|
|
|
| f0(x,y)
|
|
|
|
| Константа нуль
|
|
| f1(x,y)
|
|
|
|
| Произведение (конъюнкция)
| x∙y; xÙy;x&y
|
| f2(x,y)
|
|
|
|
| Функция запрета по y
| xDy
|
| f3(x,y)
|
|
|
|
| Переменная x
| x
|
| f4(x,y)
|
|
|
|
| Функция запрета по x
| yDx
|
| f5(x,y)
|
|
|
|
| Переменная y
| y
|
| f6(x,y)
|
|
|
|
| Сумма по модулю 2 (логическая неравнозначность)
| xÅy
|
| f7(x,y)
|
|
|
|
| Логическое сложение (дизъюнкция)
| x+y; xÚy
|
| f8(x,y)
|
|
|
|
| Операция Пирса (стрелка Пирса)
| x¯y
|
| f9(x,y)
|
|
|
|
| Эквивалентность (логическая равнозначность)
| x~y
|
| f10(x,y)
|
|
|
|
| Инверсия y
| 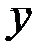
|
| f11(x,y)
|
|
|
|
| Импликация от y к x
| y®x
|
| f12(x,y)
|
|
|
|
| Инверсия x
| 
|
| f13(x,y)
|
|
|
|
| Импликация от x к y
| x®y
|
| f14(x,y)
|
|
|
|
| Операция Шеффера (штрих Шеффера)
| x½y
|
| f15(x,y)
|
|
|
|
| Константа единица
|
|
Рассмотрим некоторые переключательные функции двух аргументов.
Функция f1(x,y) называется конъюнкцией, или логическим умножением. Таблица истинности этой функции совпадает с таблицей умножения двух одноразрядных двоичных чисел. Можно ввести функцию n аргументов, соответствующую произведению n одноразрядных двоичных чисел. Такая переключательная функция равна единице тогда и только тогда, когда все ее аргументы равны единице. Для конъюнкции справедливы следующие соотношения:
x × 0 = 0;
x × 1 = x;
x × x = x;
x × y = y × x;
x ×  = 0.
= 0.
Функция f7(x,y) называется дизъюнкцией или логическим сложением. Эта функция равна нулю только в том случае, когда все ее аргументы равны нулю. Можно ввести функцию n аргументов, соответствующую логическому сложению n одноразрядных двоичных чисел. Такая переключательная функция равна нулю тогда и только тогда, когда все ее аргументы равны нулю. Для конъюнкции справедливы следующие соотношения:
x Ú 0 = x;
x Ú 1 = 1;
x Ú x = x;
x Ú y = y Ú x;
x Ú  = 1.
= 1.
Таблица истинности функции f6(x,y) совпадает с таблицей сложения двух одноразрядных двоичных чисел по модулю два. Можно ввести функцию n аргументов, соответствующую сумме по модулю два n одноразрядных двоичных чисел. Такая переключательная функция определяется следующим условием: она равна единице, если число аргументов, равных единице, нечетно, и равна нулю, если число таких аргументов четно. Приведем некоторые соотношения для суммы по модулю два:
x Å 0 = x;
x Å 1 =  ;
;
x Å x = 0;
x Å x Å x = x;
x Å y = y Å x.
Рассмотренные шестнадцать функций двух аргументов (будем называть их элементарными) позволяют строить новые переключательные функции следующим образом:
· путем перенумерации аргументов;
· путем подстановки в функцию новых функций вместо аргументов.
Функцию, полученную из функций f1, f2, …, fk путем применения (возможно многократного) этих двух правил, будем называть суперпозицией функций f1, f2, …, fk. Например, имея элементарные функции инверсии, конъюнкции, дизъюнкции, импликации, запрета, сложения по модулю два, можно составить новую переключательную функцию:
f (x,y,z) = ((  Úy)Dz)Å((y®z)×x).
Úy)Dz)Å((y®z)×x).
Используя таблицы, определяющие элементарные функции, можно задавать в виде таблицы любую переключательную функцию, являющуюся суперпозицией этих функций.
Пример 2.1. Представить в виде таблицы функцию
f (x,y,z) = ((  Úy)Dz)Å((y®z)×x).
Úy)Dz)Å((y®z)×x).
Решение. Функцию f (x,y,z) будем представлять последовательно, записывая в столбцы табл. 1.5 промежуточные результаты, получаемые после выполнения каждой операции:
Таблица 1.5
Таблица истинности функции f (x,y,z) = ((  Úy)Dz)Å((y®z)×x).
Úy)Dz)Å((y®z)×x).
| X
| y
| z
| 
|  Ú y Ú y
| (  Ú y)Dz Ú y)Dz
| y® z
| (y® z)×x
| ((  Ú y)Dz)Å
((y® z)×x) Ú y)Dz)Å
((y® z)×x)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|





 — инверсия x;
— инверсия x; — инверсия y;
— инверсия y;