Второй метод получения минимальных КНФ

 

Этот метод полностью опирается на преобразования дизъюнктивных форм переключательных функций. Алгоритм заключается в следующем.

1. Записывают дизъюнкцию всех конституент единицы, которые не входят в СДНФ заданной функции.

Если функция задана таблицей, то в эту форму войдут конституенты единицы, соответствующие наборам аргументов, на которых функция равна нулю. Если функция задана аналитически, то вначале находят ее совершенную ДНФ, а затем записывают дизъюнкцию всех конституент, которые не вошли в эту функцию. Можно показать, что полученная таким образом форма будет совершенной дизъюнктивной нормальной формой заданной функции, взятой с отрицанием.

2. Находят минимальные ДНФ по рассмотренным алгоритмам.

3. От полученных минимальных форм берут отрицания, и после пре­об­ра­зований по формулам де Моргана получают конъюнктивные формы, которые будут минимальными.

Для обоснования приведенного алгоритма получения минимальной КНФ доста­точно доказать два положения.

1. Дизъюнкция всех конституент единицы, не входящих в совершенную дизъюнктивную нормальную форму данной функции f (x ₁, x ₂, …, x_n), является отрицанием данной функции .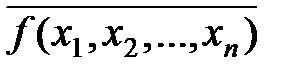

2. Преобразования по формулам де Моргана минимальной дизъ­юнк­тивной нормальной формы функции 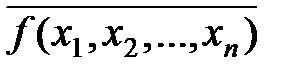приводят к получению минимальной конъюнктивной нормальной формы функции f (x ₁, x ₂, …, x_n).

Прежде всего заметим, что дизъюнкция всех конституент единицы тож­дественно равна единице. Действительно, для любого набора аргументов в такой дизъюнкции найдется конституента, равная на этом наборе единице. Но если одно логическое слагаемое ДНФ равно единице, то равна единице и вся дизъюнктивная форма. Поэтому справедливы такие, например, соот­но­шения:

,

.

В общем виде

, (2.5)

где n – число аргументов.

Рассмотрим некоторую ПФ, заданную в СДНФ:

, (2.6)

где m – число наборов, на которых ПФ равна единице.

Обозначим конституенты единицы, не входящие в последнее выра­же­ние, через , где p = 2 ⁿ – m – число наборов, на которых функция равна нулю. Тогда на основании соотношения (2.5)

.

Учитывая (2.6), получим

.

Сравнивая последнее соотношение с тождеством х ₁Ú = 1, которое можно записать в форме

,

получим

,

что и требовалось доказать.

Преобразования по формулам де Моргана не изменяют число букв в выражении для ПФ. Поэтому если взять отрицание от минимальной ДНФ функции , то полученная после преобразования по формулам де Моргана конъюнктивная форма также будет минимальной, но уже для функции .

Если предположить, что эта форма не является минимальной, то существует другая конъюнктивная форма, содержащая меньшее число букв. Тогда, взяв от нее отрицание и применив формулы де Моргана, получим дизъ­юнктивную форму с меньшим числом букв, чем в минимальной. Это противоречит определению минимальной формы и, следовательно, пред­по­ло­жение о том, что полученная конъюнктивная форма не является мини­мальной, не верно.

 

Пример 2.9. Найти минимальную конъюнктивную форму ПФ, заданной таблицей истинности (табл. 2.4).

 

Таблица 2.4.

Таблица истинности

Номер набора
x1
x 2
x 3
f (x 1, x 2, x 3)

 

1. Запишем дизъюнкцию кон­ституент единицы, соответ­ствующих набо­рам, на ко­торых функция равна нулю:

.

2. Выполним операции неполного склеивания и поглощения, после чего получим сокра­щен­ную ДНФ функции :

.

3. Испытывая импликанты, обнаружим, что вторую импликанту можно исключить (при x ₂ = 1, x ₃ = 0, выражение 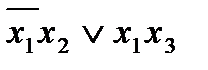º 1), т.е. минимальная ДНФ функции имеет вид

.

Использовав формулу де Моргана, получим минимальную КНФ заданной функции:

.

 

Пример 2.10. Найти минимальную конъюнктивную нормальную форму функции

.

1. Находим СДНФ:

.

2. Записав дизъюнкцию конституент единицы, не вошедших в преды­ду­щее выражение, получим СДНФ функции :

.

3. Сокращенная ДНФ имеет вид

.

4. Находим минимальные формы функции , построив импликантную матрицу (табл.2.5).

 

Таблица 2.5

Импликантная матрица

Импли- канта	Конституента
x 1 x 2 x 3	x 1 x 2 x 3	x 1 x 2 x 3	x 1 x 2 x 3	x 1 x 2 x 3
x 1 x 3	*	*
x 1 x 2		*	*
x 2 x 3			*		*
x 1 x 3				*	*

 

1) .

2)

Воспользовавшись формулой де Моргана, получим две мини­маль­ные КНФ:

f (x ₁, x ₂, x ₃) = (x ₁Ú x ₃)(x ₂Ú x ₃)(x ₁Ú x ₃).

f (x ₁, x ₂, x ₃) = (x ₁Ú x ₃)(x ₁Ú x ₂)(x ₁Ú x ₃).