Цель работы:Определение технологических показателей при разработкенефтяных месторождениях с использованием интеграла Дюамеля.
Интеграл Дюамеля имеет вид:
m t ¶ q
pкон ( t )= p ¥-2 p kh ×ò ¶ l зв f (1, t - l ) d l
Данный интеграл используется для расчета изменение давления на контуре при переменном во времени qзв = qзв( τ ) (рис.6).
q зв

qзв2
qзв1
qзв0
λ 1 λ2 λ3 λ
Рисунок 6. Схема изменения давления на контуре питания во времени
Задача 9. Внешний и внутренний контуры нефтеносности однопластового нефтя ого месторождения имеют форму, близкую к окружностям (рис. 14). Площадь месторождения можно представить в виде круга радиус м R = 2000 м. Нефтяная залежь окружена обширной водоносной областью, из к торой в нефтеносную часть пласта поступает вода при снижении пластового давления в процессе разработки месторождения.
Начальное пластовое давление р 0 =20 МПа, давление насыщения нефти газом рнас =9МПа,газосодержание Г 0=50м3/т.
По данным гидродинамических и лабораторных исследовании установлено, что средняя проницаемость как нефтеносной, так и водоносной частей пласта одинакова и составляет 0,5∙10-12 м2. Толщина пласта в среднем h =10м;средняя пористость т= 0,3;начальная нефтенасыщенностьsН0=0,95;насыщенность пласта связанной водой Sсв=0,05. Вязкости нефти и воды в пластовых условиях равны соответственно: µн= 2,0 мПа∙с, µв =1,0 мПа∙с. Плотность пластовой нефти ρн =0,85 т/м3, воды ρн=1,0 т/м3. Объемный
коэффициент нефти bн = 1,2. Коэффициент упругоемкости пласта β = 5∙10-10 Па-1.
Средний дебит жидкости одной скважины qж= 69,1 м3/сут.
Месторождение разбуривается по равномерной сетке.
Добыча жидкости из месторождения изменяется во времени следующим образом:
qж(t) = a 0 t при 0≤ t £ t *
qmax при t f t *
где t * — время ввода месторождения в разработку (t * = 3 года); a 0 = 0,667∙106 м3/год2. Коэффициент эксплуатации скважин λэ = 0,9.
Для рассматриваемого месторождения известны данные зависимости текущей обводненности продукции v от отношения Qн = Qн / Nн (Qн -

накопленная добыча нефти, Nн — извлекаемые запасы н фти). Считается, что эта зависимость будет справедливой в течение всего рассматриваемого срока разработки.
Требуется определить в условиях разработки месторождения при упругом режиме в законтурной области пласта:
1) изменение в процессе разработки за 15 ет (по годам) среднего пластового давления в пределах нефтяной залежи;
2) изменение добычи нефти, воды, текущей нефтеотдачи и обводненности продукции при заданной динамике до ычи жидкости в течение 15 лет.
Решение.
1. Определение запасов нефти и газа, числа скважин и темпа разработки. Геологические з п сы нефти определим объемным методом по формуле
Gн=Shm(1-Scв)
где S — площадь залежи, равновеликая площади круга с радиусом R( S=πR2=3,14∙22∙106= 12,56∙106м2).
Тогда запасы нефти
Gн=12,56∙106 ∙10∙0,3(1-0,05) =35,8∙106 м3
или в поверхностных условиях
Gн* =35,8∙106ρн/bн= 35,8∙106∙0,85/ 1,2 =25,4 млн. т.
Определим максимальный дебит жидкости, получаемый в конце периода разбуриваиия месторождения.
Имеем
qmax=α0t*=0,667∙106∙ 3 =2∙106 м3/год.
Число скважин, которые необходимо пробурить для отбора из месторождения qmax=2∙106 м3/год, определим с учетом коэффициента эксплуатации скважин, указанного в условиях задачи.
Получаем
| n =
| q max
| =
| 2×106
| = 88
|
|
| lэ 365 qж
| 0,9×365×69,1
|
|
Вычислим параметр плотности сетки скважин. Имеем
| Sс =
| S
| =
| 12,56×106
| = 14,27×104
| м 2
|
|
| n
|
|
| скв
|
|
|
|
|
|
|
2. Расчет изменения среднего пластового давления во времени.Аппроксимация решения Карслоу и Егера, Ван Эвердингена-Херста, сделанная Ю. П. Желтовым была применена при решении задачи 2.3, в которой рассматривался приток воды из законтурной области пласта к нефтяной залежи круговой формы с постоянным дебитом.
Однако по условию данной задачи в период разбуривания месторождения объемы воды, поступающей из законтурной области, и, следовательно, отбираемой жидкости из пласта — переменные во времени.
Поэтому для расчета давления на контуре нефтяного месторождения Pкон(t) необходимо использовать интеграл Дюамеля, согласно которому
|
| mв t
| dqж (q)
|
|
|
| Pкон(t)= р 0 -
|
| ò0
|
| f (t - q) dq
|
|
| 2 pkh
| dq
|
|
Для дальнейших расчетов удобно ввести в рассмотрение безразмерное время τ в виде
хt
τ= R 2

В этом случае интеграл Дюамеля запишется следующим образом:
|
| mв t
| dqж (l)
|
|
|
|
| Pкон(t)= р 0 -
|
| ò0
|
|
| f (t - l) dl
|
|
| 2 pkh
|
| dl
|
|
| В условии задачи qж з висит от физического времени t. В интеграл же
|
|
|
|
|
|
| dqж (l)
|
|
|
|
|
|
| Поэтому найдем зависимость qж = qж ( t ) или, что
|
|
| необходимо подставить
|
| dl
|
|
|
то же самое, qж = qж ( l ).Имеем
dqdtж = dqdtж - ddtt = dqdtж - Rx 2
О сюда
a = dqж - x = dqж - a 0 R 2 0 dt R 2 dt x
| р
|
| -
| m
| a
|
| R 2
|
|
|
| в
|
|
|
|
|
| 2 pkhx J(τ)
|
|
| Pкон(τ)=
|
|
|
| | | | | | | | | |
t
J(τ)= ò0 f ( t - l ) d l
Следовательно, для расчета давления на контуре Pкон(τ) в период
нарастающего отбора жидкости из месторождения, т.е при 0≤ t £ t *, необходимо определить интеграл J(τ).
Имеем
J(t) = ò0 t 0,5[1- (1+ (t - l)-3,81 ]+1,12log[1+ (t - l)] dl
Обозначим
| t
| dl
|
|
|
|
| J = ò0
| [1- ( t - l )3,81
| ] J = ò t ln[1+ (t - l)] dl
|
|
|
|
|
|
|
|
|
|
|
|
Вычисляя интегралы, получаем
J1=0,356[1- (1+ t)-2,81 ]
J2 = (1+ t)log(1+ t) - t
Таким образом, для J (t) имеем выражение J(τ)=0,5 t - 0,178[1- (1+ t)-2,81 ]+ 0,4871(1+ t) - t
За среднее пластовое давление в нефтяной залежи приним ем P=0,9Ркон Окончательно для расчета изменения среднего пластового давления в
нефтенасыщенной части месторождения получаем формулу
D p (t)=0,9[ р - р (t)]= 0,1432 mвa 0 R 2

0 кон khx
{0,5 t - 0,178[1- (1+ t)-2,81 ]+ 0,487[(1+ t)log(1+ t) - t ]}
хt
Эта формула справедлива только при 0≤ t £ t * (τ= R 2) Чтобы получить формулу для расчета D р ( t ) для периода постоянной добычи жидкости, т. е. при

τ f τ*, необходимо из данного выражен я вычесть такое же выражение, но зависящее не от τ, а от разности τ-τ*.
Таким образом, при τf τ *
| D р (t)=
| 0,1432 mвa 0 R 2
| × [J(τ)- J(τ- *)]
|
|
| khx
|
|


Рассчитаем изме е ие cреднего пластового давления для некоторых значений време и разработки месторождений.
Определим к эффициент пьезопроводности х. Имеем
|
| k
| =
|
| 0,5×10-12
| = 1 м 2 / с
|
|
| х= mв b
| 10-3 ×5×10-10
|
|
|
|
|
|
При t=1 год=0,31536∙108 с получаем следующее значение без-разм рного времени:
хt =1×0,31536×108=7,884
τ= R 2 4×106
При этом
D р =0,1432 mвa 0 R 2×
khx
J (7,884)= 0,5∙7,884 —0,178(1 —8,884-2,81) + 0,487 (8,884 In 8,884 - 7,884)=9,373.
Тогда D р (7,884) = 0,0768∙9,373 = 0,72 МПа.
Определим изменение среднего пластового давления в нефтяной залежи при τf τ*. Например, при t = 4 года τ=31,54. Для J (τ) получаем
J (31,54) =0,5∙31,54 – 0,178 + 0,487 (32,54 ln(32,54-31,54))= 55,41;J(τ-τ*)=J(7,884)=9,373
Тогда
D р (4) = 0,0768∙55,41-0,0768∙9,373 = 3,536 МПа.
В таблице показано изменение среднего пластового давления в нефтяной
залежи D р в различные моменты времени ее разработки. Из рис. 7 видно, что спустя 15 лет после начала разработки нефтяного месторождения пластовое давление хотя и снизилось примерно на 5 МПа, однако оно еще превышает давление насыщения (рнас = 9 МПа). Следовательно, разр ботка нефтяной залежи в течение указанного срока происходила при упругом режиме.

Рисунок 7. Графики изменен я параметров в процессе разработки залежи нефти
3. Расчет изменения добычи нефти и воды во времени при заданном отборе жидкости из пл ста.
По условию зад чи задана зависимость текущей обводненности ν продукции, получаемой из залежи, от относительной суммарной добычи нефти
или относительн й выработки извлекаемых запасов нефти Qн Если, как указано

в условии задачи, эта зависимость не будет изменяться в процессе разработки нефтяного место ождения, то можно использовать метод расчета показателей разрабо и, аналогичный известному методу — «по характеристикам выт сн ния нефти водой».
Относительная суммарная добыча нефти Qн есть частное от деления накопленной к моменту t времени разработки добычи нефти на количество извлекаемых запасов, т. е.

Qн = Qн
Nн
где
Qн =ò0 t qн (l)d l
Текущая обводненность продукции скважин определяется следующим соотношением:
где qв — дебит воды, добываемой одновременно с нефтью из всех скважин; qн — дебит нефти.
| Понятно, что
| qн = qж (1- n )Так как кривая на рис. 15выражает
|
|
| зависимость ν= ν(
| Qн
|
| ) то Q н=
| Qн
| (ν)
|
|
| Поскольку
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ò0 t qж (1- n) dl
|
|
|
| Q
|
|
|
| N
|
|
|
| н =
|
|
| н
|
|
|
|
|
|
|
|
|
| Получим
|
|
|
|
|
|
|
|
|
|
| dQн
|
| =
| qн (t)
| =
|
|
|
| qж (t)(1- n)
|
|
|
| dt
|
| Nн
|
|
|
|
|
|
|
| Nн
|
|
|
|
|
|
|
| | | | | | | | | | | | | | | | | |
Из предыдущего равенства имеем
dQн dn = 1 q (t)(1- n)
dn dt Nн ж
Разделим переменные в предыдущем равенстве:
Qн ¢( n ) dn = 1 qж (t) dt
1- n Nн
Интегрируя обе части полученного уравнения в пределах изменения обводненности до заданного значения и соответствующего времени разработки, получим
| n
|
|
| (x)
|
|
|
|
|
|
| Qн ¢
| dx =
| t
| qж (l) dl
|
|
| ò0 1- x
| N
| ò0
|
|
|
|
|
|
Интеграль е соотношение позволяет получить искомую зависимость обводненности т времени разработки. Это можно сделать путем аппроксимации данных на рис. 15 некоторой функцией.
В ачестве аппроксимирующей функции используем выражение, получ нное на основании квадратичной аппроксимации функции Баклея—
Л вер тта:
|
|
|
|
|
| a
| n
|
|
|
|
|
|
| Qн ¢
| (n) =
|
|
|
|
|
|
|
|
|
| mв
|
|
|
|
|
|
|
| a n +
|
|
|
|
|
|
|
|
|
| mн
|
|
|
|
|
|
|
|
| 1- n
|
|
|
|



Теория вытеснения нефти водой, развитая Баклеем и Левереттом, изложена, например, в [2].
Перепишем, введя обозначение
m = mв 1
mн a
где а — некоторый постоянный коэффициент, зависящий от свойств коллектора.
Qн ¢( n )=1+ m 11- n


n
Коэффициент а определим по известным величинам  и Qн ¢ из выражения Выберем три точки с координатами ν- Qн
и Qн ¢ из выражения Выберем три точки с координатами ν- Qн
1) ν1=0,3
2) ν2=0,5
3) ν3=0,8
4) Qн =0,58
5) Qн 2=0,68
6) Qн 3=0,82
Вычислим коэффициенты:
|
|
|
|
|
| 1- 0,3
|
|
|
|
|
|
|
| a =
|
|
|
|
|
| 0,3
|
|
|
| = 1,0547
|
|
|
|
|
|
|
|
|
| -1)
|
|
| 2(
|
|
|
|
|
|
|
|
| 0,58 н
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1- 0,5
|
|
|
|
|
|
|
| a =
|
|
|
|
|
| 0,5
|
|
|
|
| = 1,0625
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2(
|
|
|
| -1)
|
|
|
|
|
| 0,68 н
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1- 0,8
|
|
|
|
|
|
|
| a =
|
|
|
|
|
| 0,8
|
|
|
| = 1,1389
|
|
|
|
|
|
|
|
|
| -1)
|
|
| 2(
|
|
|
|
|
|
|
|
| 0,82 н
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Определим среднее значение:
|
|
|
|
| Тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| m =
|
|
|
|
| = 0,46
|
|
|
|
|
| 2 ×1,0854
|
|
| | | | | | | | | | | | | | | | |



Формула зависимости суммарной относительной добычи нефти от текущей обводненности для заданных условий имеет вид

Произведем вычисления по полученной зависимости, результаты которых сведем в таблице. По результатам построена кривая. Видно, что расчетная зависимость хорошо описывает исходные данные.
Рассмотрим интеграл в левой части данного соотношения. Представим его как
| ò0 n
|
|
| (х) dx
|
|
|
|
| Qн ¢
| = ò0 n
| f ¢(x) f (x) dx
|
|
|
| 1 - x
|
|
|
|
|
|
|
|
где
f ¢(x) = Qн ¢(x); f (x) = 1-1 x
Таблица Расчётные данные
| ν
|
|
|
| u*
|
|
|
|
|
|
|
| v**
| J(ν)
| J(t)
| t, год
|
|
|
|
|
|
|
|
| Qн
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,01
|
|
|
|
|
|
| 0,179
| 0,574
| 0,18
|
| 1,6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,05
|
|
|
|
|
|
| 0,333
| 2,005
| 0,237
| 0,237
| 3,8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,1
|
|
|
|
|
|
| 0,42
| 1,38
| 0,412
| 0,412
| 5,6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,2
|
|
|
|
|
|
| 0,521
| 0,92
| 0,55
| 0,55
| 6,9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,3
|
|
|
| 2,33
|
|
| 0,587
| 0,702
| 0,639
| 0,64
| 7,8
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,4
|
|
|
| 1,5
|
|
| 0,61
| 0,563
| 0,719
| 0,72
| 8,6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,5
|
|
|
| 1,0
|
|
| 0,685
| 0,46
| 0,801
| 0,8
| 9,5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,6
|
|
|
| 0,667
|
|
| 0,727
| 0,376
| 0,89
| 0,9
| 10,4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,7
|
|
|
| 0,429
|
|
| 0,769
| 0,301
| 1,016
| 1,02
| 11,6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,8
|
|
|
| 0,25
|
|
| 0,813
| 0,23
| 1,196
| 1,2
| 13,5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,9
|
|
|
| 0,111
|
|
| 0,867
| 0,153
| 1,581
| 1,6
| 17,4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,96
|
|
|
| 0,053
|
|
| 0,904
| 0,106
| 2,101
| 2,1
| 22,6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,98
|
|
|
| 0,02
|
|
| 0,938
| 0,065
| 3,214
| 3,214
| 33,9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0,99
|
|
|
| 0,01
|
|
| 0,956
| —
| —
| —
| —
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| * u =
| 1- n
| ** s =
|
|
|
| 1- n
|
|
|
|
|
|
| m
|
|
|
|
|
|
|
| n
|
|
|
| n
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Используем правило интегрирования но частям. Выполним необходимые вычисления:
df (x)= dx

(1- x)2
f (x) = Qн ¢(n);

Так как
ò0 n f ¢(x) f (x) dx = f ¢(x) f (x)ò0 n -ò0 n f ¢(x) f (x) dx;
получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n Q
| ¢
| (х)
|
|
|
|
|
| dx
| n
|
|
|
|
| dx
|
|
| ò0
|
| н
|
| dx =
|
|
|
|
|
|
| - ò0
|
|
|
|
|
|
|
|
|
|
| 1- x
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1- n
|
|
|
|
|
|
| 1- x
|
| )(1- x 2)
|
|
|
| (1+
| m
|
|
|
| )(1- n)
| (1
| +
| m
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n
|
|
|
|
|
|
| x
|
|
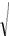
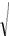
Интеграл в правой части равенства легко приводится к табличному вид у с помощью подстановок:
|
|
| u =
| 1- n
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n
|
|
|
| ; l =
|
| u
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n
|
|
|
|
|
|
|
|
|
| dx
|
|
|
|
|
|
|
|
|
|
|
|
|
| n
|
|
|
|
| dl
|
|
|
|
|
|
|
|
|
|
|
|
|
| ò0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| = -2ò0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

































 и Qн ¢ из выражения Выберем три точки с координатами ν- Qн
и Qн ¢ из выражения Выберем три точки с координатами ν- Qн