Р. И. МАКАРОВ
Модели и методы планирования
Экспериментов,
Обработки экспериментальных данных
Курс лекций по дисциплине «Модели и методы планирования экспериментов, обработки экспериментальных данных»
для магистрантов по направлениям:
09.04.02- Информационные системы и технологии, программа
подготовки - Информационные системы и технологии;
09.04.04 - Программная инженерия, программа подготовки
Разработка программно-информационных систем
Учебное электронное издание
Владимир – 2016 г.
Курс лекций по дисциплине «Модели и методы планирования экспериментов, обработки экспериментальных данных» предназначен для подготовки магистров по дисциплинам общенаучного цикла, вариативной части, направления 09.04.02- Информационные системы и технологии, программа подготовки - Информационные системы и технологии; 09.04.04 - Программная инженерия, программа подготовки - Разработка программно-информационных систем.
Курс знакомит магистрантов с моделями и методами планирования экспериментов и обработки экспериментальных данных.
Конспект лекций позволяет освоить методы планирования экспериментов, сбора статистических данных с объектов моделирования, методы построения моделей сложных систем и нахождения экстремальных условий функционирования объектов, методы уменьшения размерности разрабатываемых моделей, методы анализа временных рядов и их прогнозирования.
Содержание
Лекция 1 Место планирования экспериментов в исследовании систем 3
Лекция 2. Полный факторный эксперимент. Дробные реплики 12
Лекция 3 Крутое восхождение по поверхности отклика 24
Лекция 4 Ротатабельное планирование второго порядка 32
Лекция 5 Исследование почти стационарной области 39
Лекция 6 Множественный регрессионный анализ 51
Лекции 7 Особенности планирования промышленного эксперимента 63
Лекция 8 Рекуррентные алгоритмы построения математического описания дрейфующих объектов. Метод текущего регрессионного анализа 74
Лекция 9 Методы анализа больших систем. Компонентный и факторный анализы 79
Лекция 10 Системы линейных уравнений 93
Лекция 11 Дисперсионный анализ 105
Лекция 12 Модели временных рядов и статистические оценки взаимосвязи временных рядов 115
Лекция 13 Прогнозирование временных рядов 134
Список используемой литературы 145
Лекция 1 Место планирования экспериментов в исследовании систем
1. Основы теории планирования эксперимента
Можно выделить два основных направления в теории планирования эксперимента [1]:
1) Планирование экстремальных экспериментов;
2) Планирование эксперимента по выяснению механизма явлений.
Первый тип применяется для поиска условий, при которых прогресс удовлетворяет некоторому критерию поиска оптимальности (разработка новых процессов).
Второй тип находи функцию, определяющую связь между выходной переменной объекта и величинами, влияющими на ход изучаемого процесса входными переменными. Т.е. ставится задача нахождения математической модели данного процесса. В данном курсе мы уделим значительное внимание довольно тщательно изученному планированию экстремальных экспериментов по поиску математических моделей, описывающих исследуемый объект (Н.П. Клепиков, С.И. Соколов Анализ и планирование экспериментов методом максимума правдоподобия. Физматгиз 1964; В.В, Федоров. Теория оптимального эксперимента, Наука, 1971 год).
Задача экспериментатора по поиску математической модели заключается в отыскании связи между измеряемыми переменными. Так как результаты наблюдений – величины случайные, то имеет смысл говорить о связи средних значений исследуемых величин с контролируемыми переменными:
 (1)
(1)
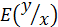 – среднее значение исследуемой величины «у» при значениях контролируемых переменных, определяемых компонентами вектора Х.
– среднее значение исследуемой величины «у» при значениях контролируемых переменных, определяемых компонентами вектора Х.
 – зависит от неизвестных параметров в 1, в 2, в m эта функция называется поверхностью отклика.
– зависит от неизвестных параметров в 1, в 2, в m эта функция называется поверхностью отклика.
Приступая к поиску математической модели (1) экспериментатор обладает априорной информацией:
1) Случай 1. Вид функции  известен, требуется определить и уточнить неизвестные параметры функции
известен, требуется определить и уточнить неизвестные параметры функции
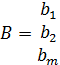 (2)
(2)
2) Случай 2. Известно, что функция  совпадает с одной из функций
совпадает с одной из функций
 (3)
(3)
Требуется определить, какая из функций является истинной, и найти неизвестный параметр B.
3) Случай 3. Вид функции  не известен. Известно, лишь, что
не известен. Известно, лишь, что  в интересующей области может достаточно хорошо аппроксимирована конечным рядом по некоторой системе наперед заданных функций. Требуется найти наилучшее описание функции
в интересующей области может достаточно хорошо аппроксимирована конечным рядом по некоторой системе наперед заданных функций. Требуется найти наилучшее описание функции  .
.
Математический аппарат планирования эксперимента при априорных сведениях (случай 1) достаточно полно разработан. Развиты эффективные методы планирования эксперимента статистического (всего эксперимента в целом) и последовательного.
Статистическое планирование заключается в использовании готовых таблиц, описывающих характеристики оптимальных планов.
Планирование по поиску истинных моделей (случай 2) появилось в последнее время, несомненно, будет совершенствоваться как с идейной, так и вычислительной точки зрения. Большинство имеющихся методов по своей природе являются последовательными.
Наиболее трудной является задача планирования эксперимента, когда функция  совершенно неизвестна (случай 3). Имеется разработки последовательного процесса поиска математической модели.
совершенно неизвестна (случай 3). Имеется разработки последовательного процесса поиска математической модели.
Рассмотрим общие требования предъявляемые к оценкам
 (4)
(4)
Целью анализа экспериментальных данных является определение оценок неизвестных параметров «В». Результаты наблюдений являются случайными величинами.
 , (5)
, (5)
где е – помеха.
Опираясь на «у» мы, вообще говоря, не можем получить истинных значений В ист для неизвестных параметров. Приходиться использовать случайные величины В, которые некоторым образом зависят от результатов наблюдений.
 (6)
(6)
Эксперименты, цель которых – поиск оценок неизвестных параметров  или неизвестной поверхности
или неизвестной поверхности  в предложении справедливости (4) мы будем называть регрессионными. Процедура поиска оценок называется регрессионным анализом.
в предложении справедливости (4) мы будем называть регрессионными. Процедура поиска оценок называется регрессионным анализом.
Чтобы оценка  имела практическую ценность, она должна обладать свойствами несмещённости, состоятельности, эффективности.
имела практическую ценность, она должна обладать свойствами несмещённости, состоятельности, эффективности.
Несмещенность. Оценки  – несмещенные, если их математические ожидания равны истинным значениям параметров:
– несмещенные, если их математические ожидания равны истинным значениям параметров:
 (7)
(7)
Состоятельность. Оценки  состоятельные, если они сходятся по вероятности к истинным значениям параметров:
состоятельные, если они сходятся по вероятности к истинным значениям параметров:
 (8)
(8)
где N – число измерений,  – любое наперед заданное положительное число.
– любое наперед заданное положительное число.
Эффективность. Несмещенные оценки  - эффективны, если имеет место неравенство:
- эффективны, если имеет место неравенство:
 (9)
(9)
где D () – дисперсионная матрица оценок  , любых других несмещенных оценок
, любых других несмещенных оценок 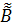 .
.
Для каждой функции  и каждого закона распределения результатов наблюдений р (у/х) – плотность функции распределения, имеются в общем случае свои «наилучшие» оценки
и каждого закона распределения результатов наблюдений р (у/х) – плотность функции распределения, имеются в общем случае свои «наилучшие» оценки  . Эта зависимость крайне неудобна на практике, т.к. требует для каждой экспериментальной ситуации свой алгоритм анализа и планирования эксперимента. Поэтому не выдерживают точного выполнения какого-либо из указанных свойств и вычисляют оценки по одному и тому же алгоритму для любого вида
. Эта зависимость крайне неудобна на практике, т.к. требует для каждой экспериментальной ситуации свой алгоритм анализа и планирования эксперимента. Поэтому не выдерживают точного выполнения какого-либо из указанных свойств и вычисляют оценки по одному и тому же алгоритму для любого вида  и р (у/х). (Распространен метод анализа экспериментов, опирающийся на вторые моменты и не использующий вид функции р (у/х). Это важно на практике, т.к. зачастую неизвестен закон распределения результатов наблюдений.
и р (у/х). (Распространен метод анализа экспериментов, опирающийся на вторые моменты и не использующий вид функции р (у/х). Это важно на практике, т.к. зачастую неизвестен закон распределения результатов наблюдений.
Движение по градиенту
Наиболее короткий путь к оптимуму – направление градиента функции отклика. Градиент непрерывной однозначной функции  есть вектор
есть вектор
 ,
,
где  – обозначение градиента,
– обозначение градиента,  – частная производная функции по i -му фактору, i, j, k – единичные векторы в направлении координатных осей.
– частная производная функции по i -му фактору, i, j, k – единичные векторы в направлении координатных осей.
Следовательно, составляющие градиента суть частные производные функции отклика, оценками которых являются, коэффициенты регрессии. Поэтому процедура движения к почти стационарной области называется крутым восхождением.
Величины составляющих градиента определяются формой поверхности отклика и теми решениями, которые были приняты при выборе параметра оптимизации, нулевой точки и интервалов варьирования. Знак составляющих градиента зависит только от формы поверхности отклика и положения нулевой точки.
Выбор шага движения по градиенту имеет значение при поиске оптимума. Небольшой шаг потребует значительного числа опытов при движении к оптимуму, большой шаг увеличивает вероятность проскока области оптимума.
Движение по градиенту начинается из нулевой точки, центра плана. Движение проводится только по значимым факторам. Функция, величины коэффициентов которой различаются не существенно, называется симметричной относительно коэффициентов. Движение по градиенту для симметричной функции наиболее эффективно. Удачным выбором интервалов варьирования можно сделать симметричной любую линейную функцию для значимых факторов. Если функция резко асимметрична (коэффициенты различаются на порядок), то выгоднее вновь поставить эксперимент, изменив интервалы варьирования, а не двигаться по градиенту.
Рассчитав составляющие градиента, получают условия мысленных опытов. Число мысленных опытов ограничивается сверху границей области определения по одному из факторов. Обычно рассчитывается 5–10 мысленных опытов.
Существует две стратегии реализации мысленных опытов. Все намеченные к реализации опыты ставятся одновременно либо последовательно по некоторой программе. Последовательный принцип заключается в том, что вначале ставятся два-три опыта, анализируются результаты и принимается решение о постановке новых опытов.
Крутое восхождение считается эффективным, если хотя бы один из реализованных опытов даст лучший результат по сравнению с наилучшим опытом серии.
Иногда приходится считаться с возможностью временного дрейфа. Между исходной серией опытов и движением по градиенту может пройти значительное время. Здесь можно рекомендовать систематическое повторение нулевых точек исходного плана, рандомизированных с точками крутого восхождения. Это дает возможность проверить гипотезу о наличии дрейфа. Чтобы исключить влияние систематических ошибок, вызванных внешними условиями (переменой температуры, сырья, лаборанта и т.д.), рекомендуется случайная последовательность при постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать во времени. Термин «рандомизация» происходит от английского слова random – случайный.
Поверхностей отклика
На практике часто приходится отыскивать условный экстремум функции отклика  при ограничениях, накладываемых другой функцией y2=φ2=(x1, x2,..xk) [2].
при ограничениях, накладываемых другой функцией y2=φ2=(x1, x2,..xk) [2].
При большом числе независимых переменных задача решается методом неопределенных множителей Лагранжа.
Метод неопределенных множеств Лагранжа сводится к решению системы уравнений:


… (9)


относительно переменных х 1, х 2,.. xk, λ при некотором фиксированном значении y 2.
Пример 3.
Для выхода реакции y 1 и чистоты продукта y 2 получены уравнения регрессии [2]:

где  – давление,
– давление, 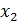 – температура химического процесса.
– температура химического процесса.
Задавшись частотой продукта у 2=90%, находим условный экстремум для функции, определяющий выход реакции у 1.
Метод неопределенных множеств Лагранжа приводит к системе уравнений:

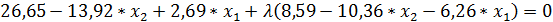
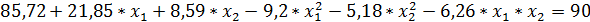
Методом скорейшего спуска были найдены три решения (табл. 2).
Анализ табличных данных показывает, что чистота продукта у 2 может быть достигнута за счет уменьшения выхода реакции у 1.
Таблица 2 – Результаты решения задачи на условный экстремум [2]
| Варианты решений
|
|
|
|

| 83,66
| 86,73
| 88,68
|

| 94,87
| 92,47
| 89,99
|

| 0,965
| 1,005
| 1,075
|

| 1,088
| 1,316
| 1,479
|
| λ
| 1,612
| 0,973
| 0,665
|
В ряде случаев при решении подобных задач сталкиваются со специфическими вычислительными трудностями, связанными с тем, что матрицы оказываются плохо обусловленными (определитель матрицы (X т X) близок к нулю). Результаты вычислений при этом становятся неустойчивыми. Имеются ряд приемов, позволяющие преодолеть эти трудности [2].
Контрольные вопросы
1. Когда возникает задача поиска оптимальных условий протекания процесса?
2. При решении задачи используется математическая модель объекта исследования. Каким свойствам должна удовлетворять математическая модель?
3. Что является параметром оптимизации, требования, предъявляемые к параметру оптимизации?
4. Что определяет поведение исследуемой системы. Требования, предъявляемые к факторным переменным?
5. В каких точках для предсказания результатов опытов используется нелинейная (квадратичная) модель?
6. Какими методами может осуществляться поиск оптимума по полученному полиному?
7. Как осуществляется поиск оптимума методом нелинейного программирования?
8. Для чего приводятся уравнения регрессии к канонической форме?
9. Как проводится анализ уравнений в канонической форме?
10. Какие виды поверхностей отклика существуют и особенности их анализа?
11. Как отыскивается условный экстремум при наличии нескольких поверхностей отклика?
12. В чем сущность метода неопределенных множеств Лагранжа?
Эксперимента
Промышленный объект исследования можно представить нижеприведенной схемой (рис.1) [4]. Независимые (факторные) переменные x 10, x 20,.. x k0 регистрируются с погрешностью измерений ei, i =1, 2,.. k. Зависимая переменная «y» «зашумлена» под влиянием неучтенных возмущающих воздействий d 1, d 2,.. d s. Эквивалентный шум, приведенный к выходной переменной, представляет случайную величину, обозначен переменной «е».
Рисунок 1 – Схема промышленного эксперимента по статистическому
описанию объекта в режиме нормального функционирования
Таким образом, при разработке модели регрессии, экспериментатор использует не точную информацию. Ниже рассматривается влияние погрешностей измерения входных и выходных переменных на точность коэффициентов регрессии и качество модели. Полагаем, что объект описывается линейной регрессионной моделью.
Допущения:
1) xi, i= 1, 2,.. k – нормально распределенный стационарный случайный процесс, обладает свойством эргодичности;
2) d 1- ds – возмущающие воздействия, независимые случайные процессы с нулевым математическим ожиданием, среди которых нет доминирующих. Не коррелированны с входными переменными;
3) Объект исследования стационарный.
Выбор степени полинома возможно:
- с использованием априорной информации об объекте;
- выбор полинома 2-го и 3-го порядка и последовательный отсев незначимых коэффициентов.
Анализа
При построении математического описания промышленных объектов приходится встречаться с фактом неконтролируемого изменения характеристик объекта во времени. Объекты, обладающие такими свойствами, называются нестационарными (дрейфующими). Причиной являются наличие неконтролируемых воздействий, значения которых не могут учитываться при построении модели объекта. Дрейф характеристик может возникать из-за изменения активности катализатора, износа огнеупоров тепловых агрегатов, изменения условий работы, влияние времен года и др. Как правило, изменение дрейфующих параметров происходит значительно медленнее процесса изменения контролируемых переменных.
В предыдущих лекциях при построении математического описания по выборке оценивались математические ожидания коэффициентов модели в предположении отсутствия дрейфа. Будем рассматривать случай, когда действительные значения коэффициентов изменяются во времени. Для этого выбирается адаптивный путь решения задачи, в котором по выборке необходимо получить помимо математического ожидания коэффициентов оценки рядя параметров, значения которых определяются неизвестными априори свойствами дрейфа [4].
При решении задачи построения математического описания дрейфующего объекта возможны ситуации двух типов:
1) по выборке наблюдений за входом и выходом объекта на некотором интервале времени от t 0 до t > t 0 необходимо найти оценки вектора коэффициентов модели, близкие к действительным значениям коэффициентов в момент t + α, где α ≥0;
2) осуществляется непрерывное слежение за изменением коэффициентов модели. В любой момент времени t требуется найти наилучшее приближение к действительным значениям коэффициентов в момент t + α.
Вторая ситуация аналогична первой при стремлении длины интервала наблюдений к бесконечности.
Компонентный анализ
Компонентный анализ является методом определения структурной зависимости между случайными переменными [5]. Идея метода заключается в замене сильно коррелированных переменных новыми переменными (главными компонентами), между которыми корреляция отсутствует. В результате его использования получается сжатое описание малого объема, несущее почти всю информацию, содержащуюся в исходных данных. Главные компоненты получаются из исходных переменных путем целенаправленного вращения, т.е. как линейные комбинации исходных переменных. Вращение производится таким образом, чтобы главные компоненты были ортогональны и имели максимальную дисперсию среди возможных линейных комбинаций исходных переменных. При этом переменные не коррелированны между собой и упорядочены по убыванию дисперсии (первая компонента имеет наибольшую дисперсию). Кроме того, общая дисперсия после преобразования остается без изменений.
Ход рассуждений при выполнении поиска главных компонент заключается в следующем. Мы предполагаем наличие некоррелированных переменных Zj (j =1… k), каждая из которых представляется нам комбинацией основных переменных (суммирование по i =1… k):
Zj = S Aj i ·X i
и, кроме того, обладает дисперсией, такой что
D (Z 1) ³ D (Z 2) ³ … ³ D (Zk).
Поиск коэффициентов Aj i (их называют весом j- й компоненты в содержании i- й переменной) сводится к решению матричных уравнений и не представляет особой сложности при использовании компьютерных программ. Но суть метода весьма интересна и на ней стоит задержаться.
Как известно из векторной алгебры, диагональная матрица [2·2] может рассматриваться как описание 2-х точек (точнее — вектора) в двумерном пространстве, а такая же матрица размером [ k·k ] — как описание k точек k -мерного пространства.
Так вот, замена реальных, хотя и нормированных переменных Xi на точно такое же количество переменных Z j означает не что иное, как поворот k осей многомерного пространства.
“Перебирая” поочередно оси, мы находим вначале ту из них, где дисперсия вдоль оси наибольшая. Затемделаем пересчет дисперсий для оставшихся k -1осей и снова находим “ось-чемпион” по дисперсии и т.д.
Образно говоря, мы заглядываем в куб (3-х мерное пространство) по очереди по трем осям и вначале ищем то направление, где видим наибольший “туман” (наибольшая дисперсия говорит о наибольшем влиянии чего-то постороннего); затем “усредняем” картинку по оставшимся двум осям и сравниваем разброс данных по каждой из них — находим “середнячка” и “аутсайдера”. Теперь остается решить систему уравнений — в нашем примере для 9 переменных, чтобы отыскать матрицу коэффициентов (весов) A [ k·k ].
Если коэффициенты Aj i найдены, то можно вернуться к основным переменным, поскольку доказано, что они однозначно выражаются в виде (суммирование по j =1… k)
X i = S Aji·Z j.
Отыскание матрицы весов A [ k·k ]требует использования ковариационной матрицы и корреляционной матрицы.
Таким образом, метод главных компонент отличается прежде все тем, что дает всегда единственное решение задачи. Правда, трактовка этого решения своеобразна.
1) Мы решаем задачу о наличии ровно стольких факторов, сколько у нас наблюдаемых переменных, т.е. вопрос о нашем согласии на меньшее число латентных факторов невозможно поставить;
2) В результате решения, теоретически всегда единственного, а практически связанного с громадными вычислительными трудностями при разных физических размерностях основных величин, мы получим ответ примерно такого вида — фактор такой-то (например, привлекательность продавцов при анализе дневной выручки магазинов) занимает третье место по степени влияния на основные переменные.
Этот ответ обоснован — дисперсия этого фактора оказалась третьей по крупности среди всех прочих. Больше ничего получить в этом случае нельзя. Другое дело, что этот вывод оказался нам полезным или мы его игнорируем — это наше право решать, как использовать системный подход.
Пример. Имеются данные, описывающие зависимость результирующей переменной «y» от факторных переменных x 1 – x 3 (таблица 5).
Требуется выделить главные компоненты и построить уравнение регрессии на главных компонентах.
Перед тем как проводить компонентный анализ, проводится анализ независимости исходных признаков. Проверяется значимость матрицы парных корреляций с помощью критерия Уилкса.
Выдвигается гипотеза: Н 0: 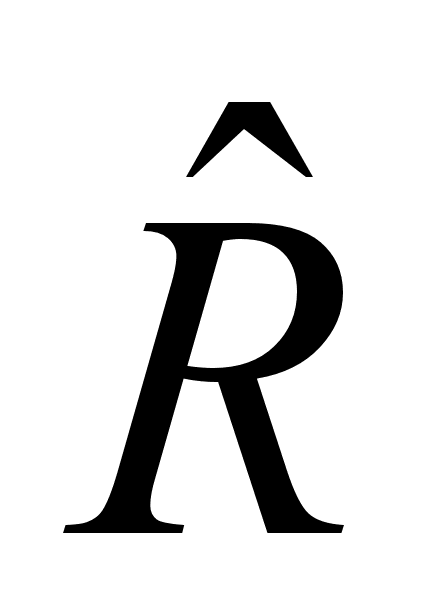 незначима и альтернативная Н 1:
незначима и альтернативная Н 1: 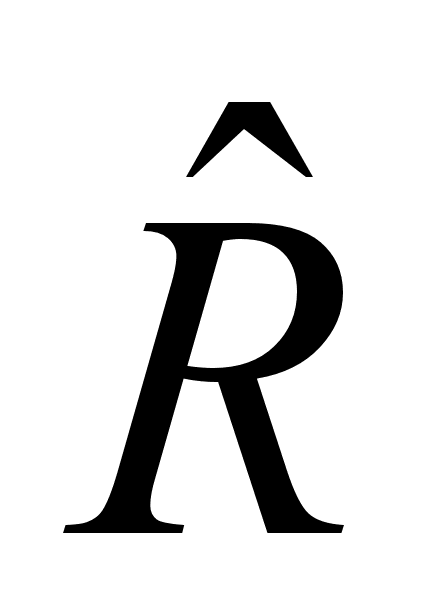 значима.
значима.
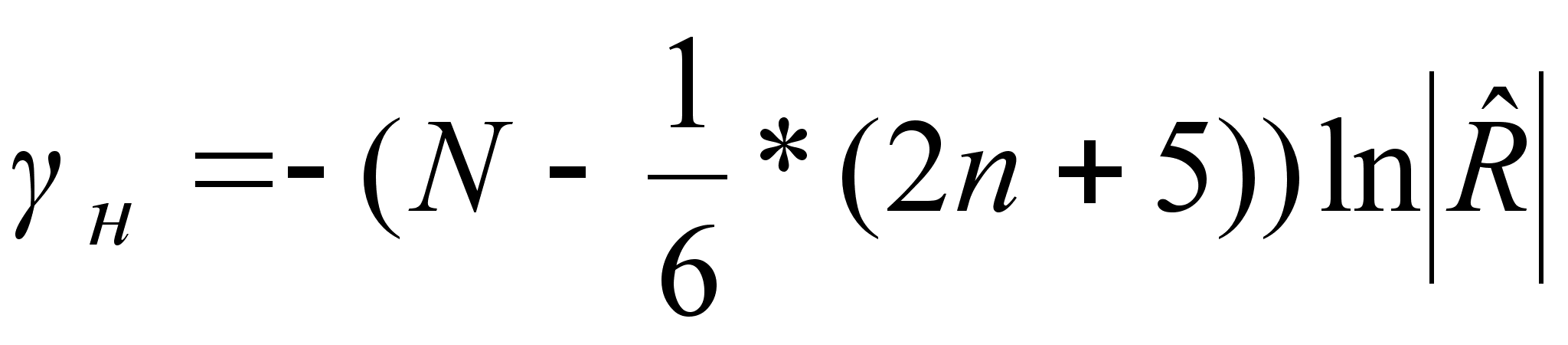
Рассчитывается статистика, которая распределена по закону 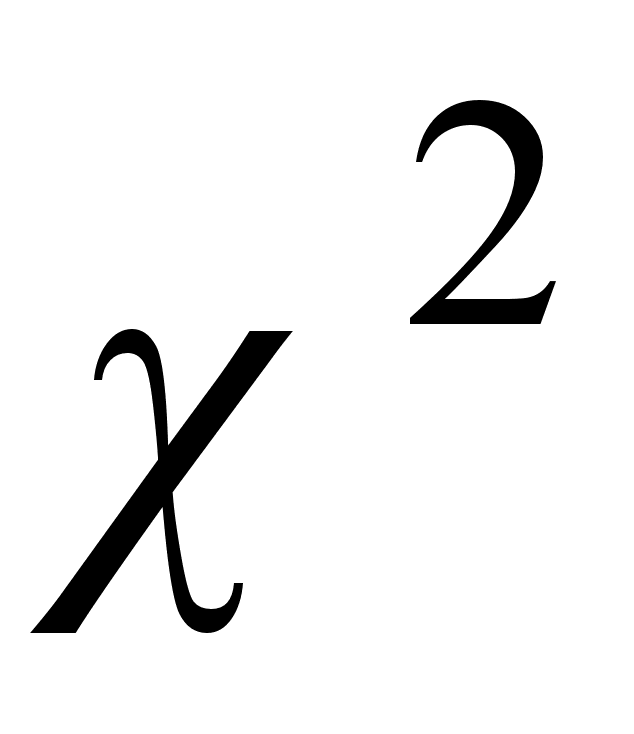 с
с 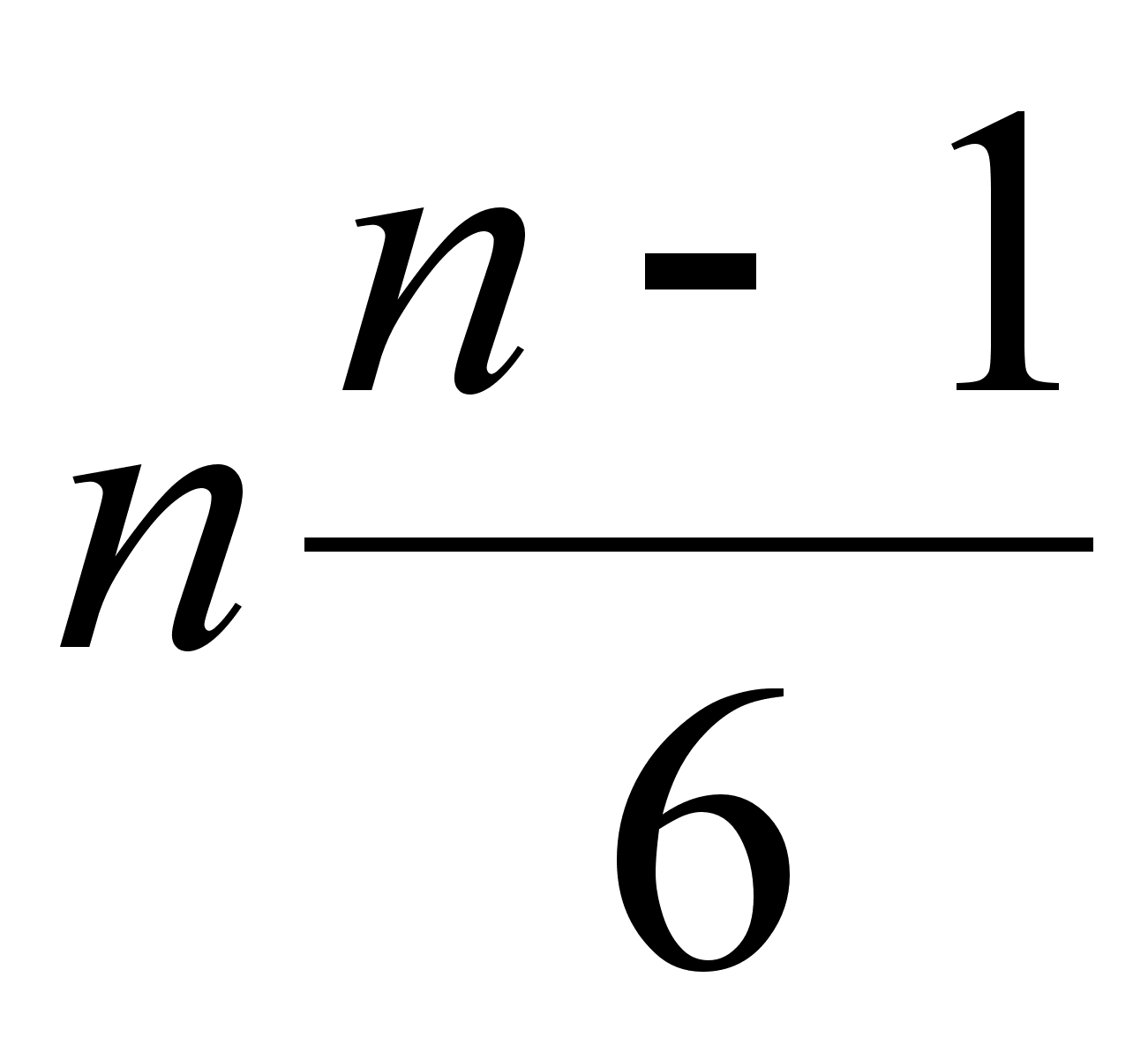 - степенями свободы. Сравнивается расчетное значение с табличным значением
- степенями свободы. Сравнивается расчетное значение с табличным значением 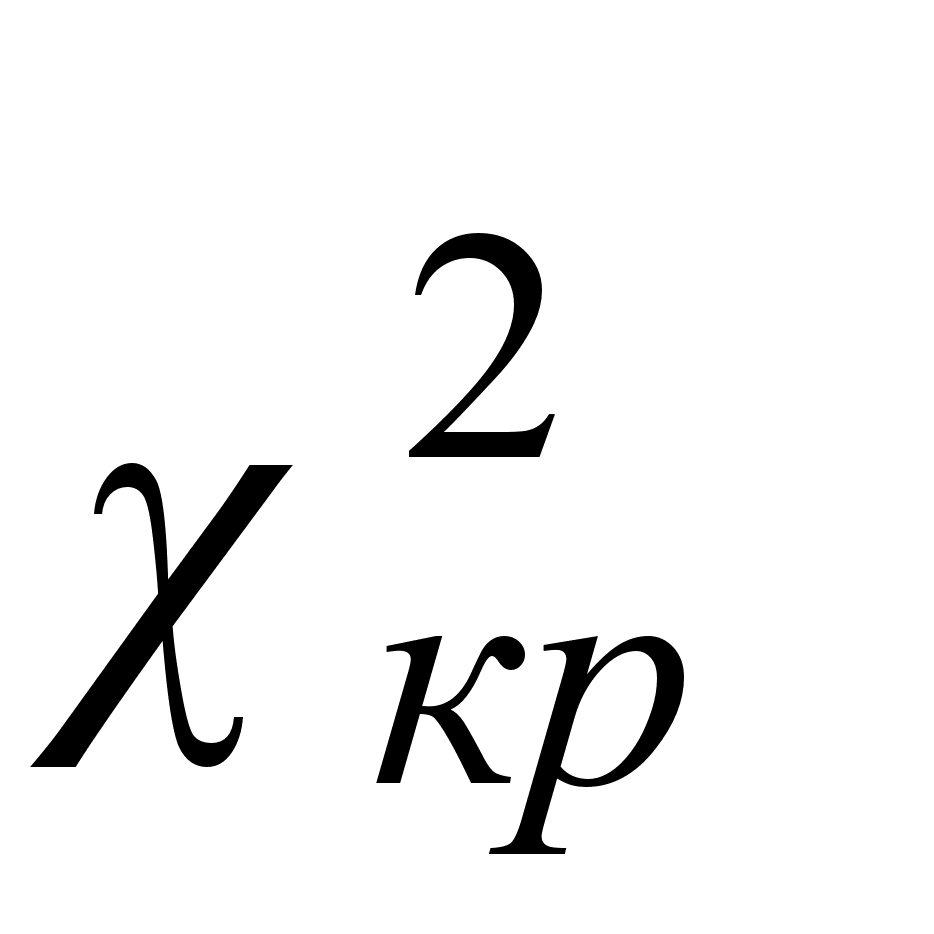 для уровня значимости α = 0,05.
для уровня значимости α = 0,05.
Таблица 5- Зависимость результирующей переменной
от факторных переменных
| х 1
| х 2
| х 3
| у
|
| 1,1
| 1,1
| 1,2
| 26,2
|
| 1,4
| 1,5
| 1,1
| 25,9
|
| 1,7
| 1,8
|
| 32,5
|
| 1,7
| 1,7
| 1,8
| 31,7
|
| 1,8
| 1,9
| 1,8
| 31,7
|
| 1,8
| 1,8
| 1,9
| 33,6
|
| 1,9
| 1,8
|
| 34,2
|
|
| 2,1
| 2,1
| 34,4
|
| 2,3
| 2,4
| 2,5
| 35,5
|
| 2,5
| 2,5
| 2,4
| 36,5
|
Если расчетное значения критерия будет больше табличного значения
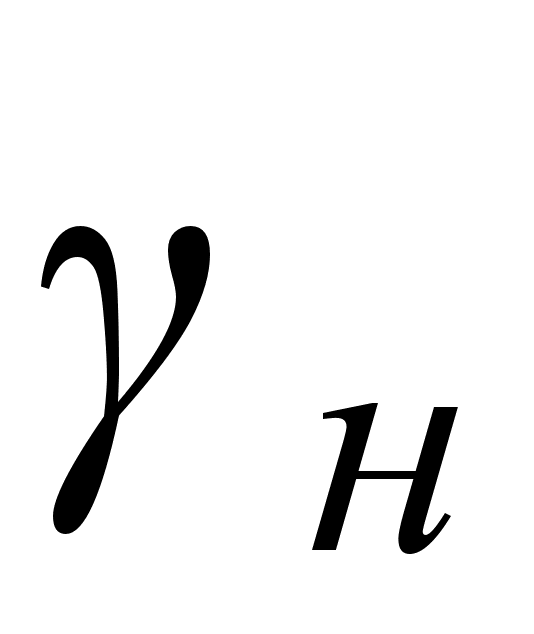 >
> 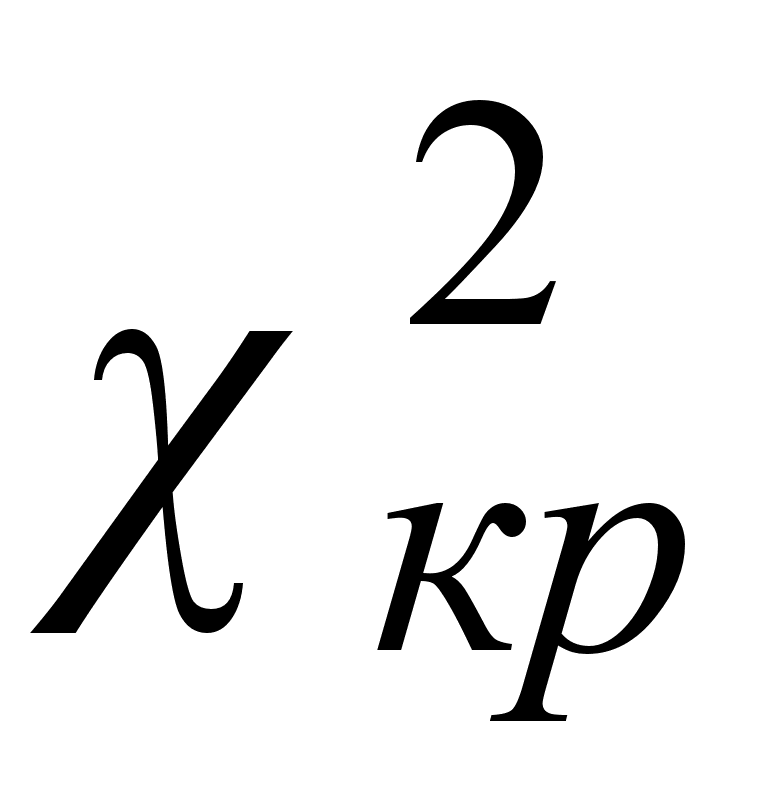 , то гипотеза Н 0 отвергается и принимается альтернативная Н 1:
, то гипотеза Н 0 отвергается и принимается альтернативная Н 1: 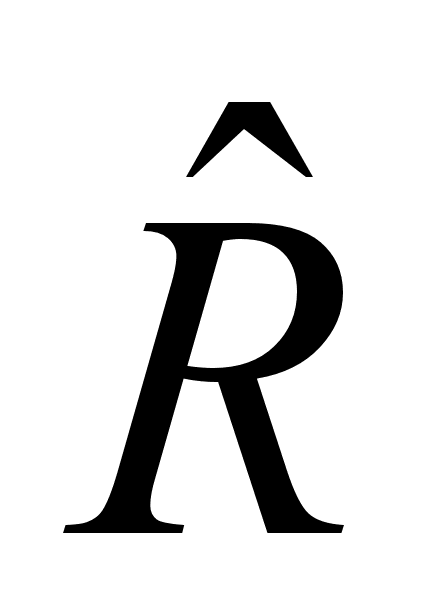 значима, следовательно, имеет смысл проводить компонентный анализ.
значима, следовательно, имеет смысл проводить компонентный анализ.
Затем поверяется гипотеза о диагональности ковариационной матрицы.
Выдвигается нулевая гипотеза:
Н 0: соv 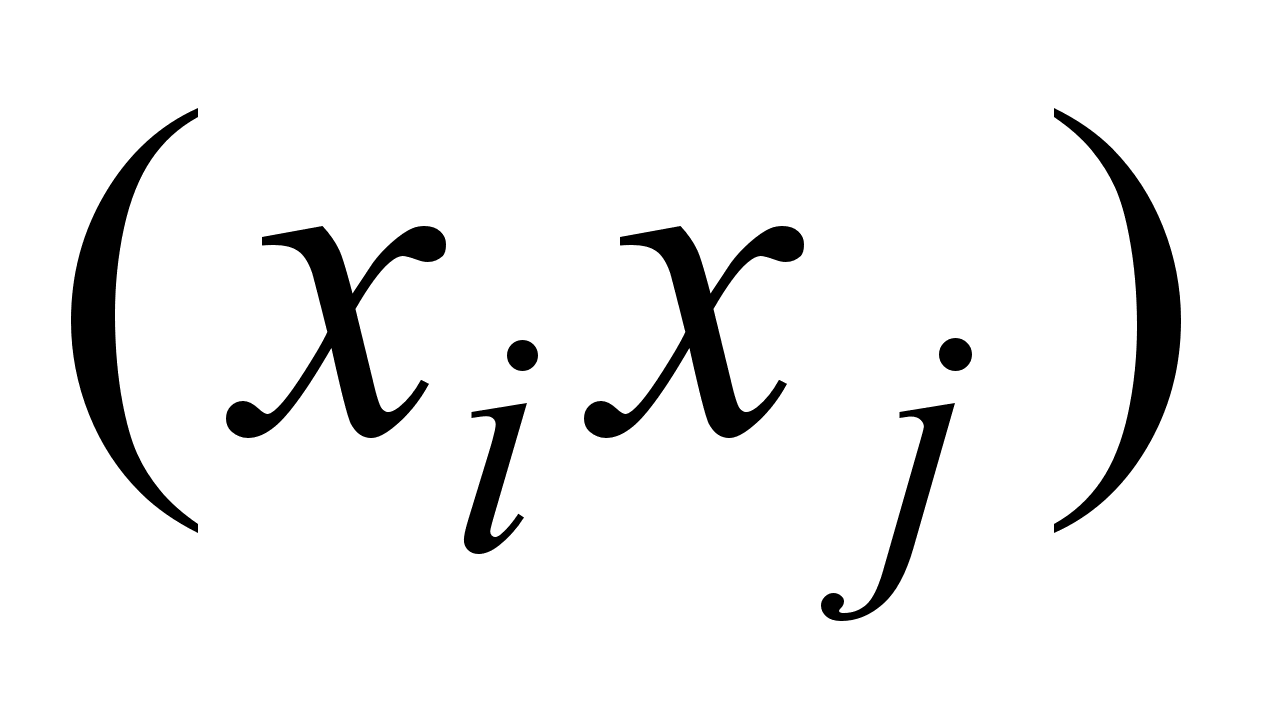 =0,
=0, 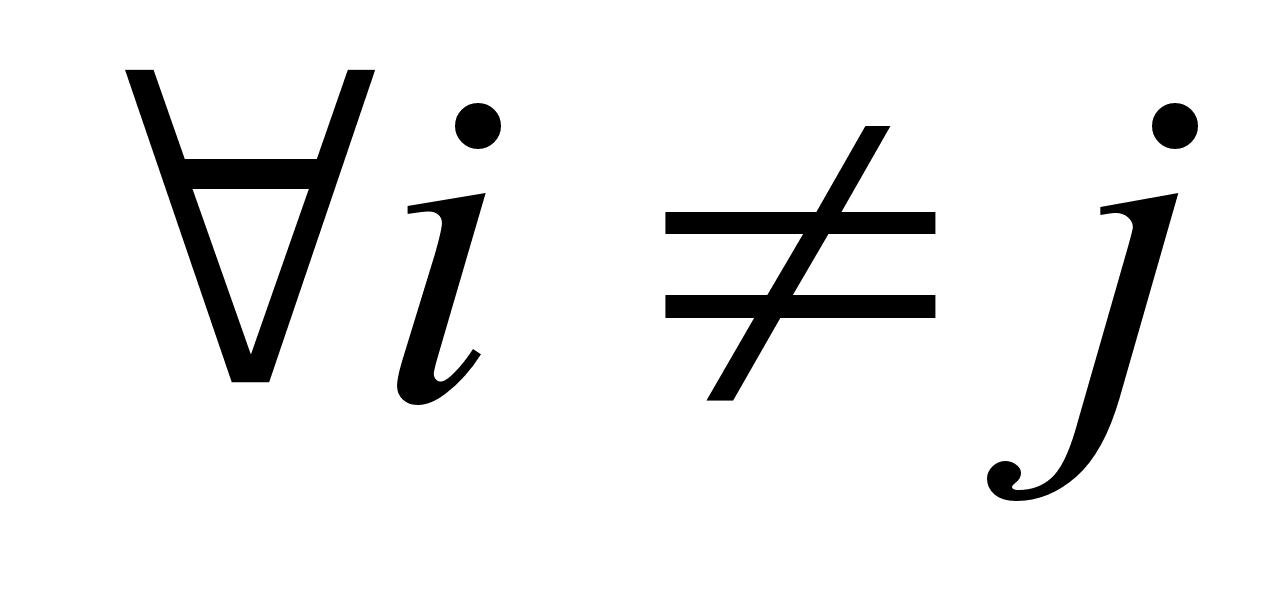 и альтернативная Н 1: соv
и альтернативная Н 1: соv 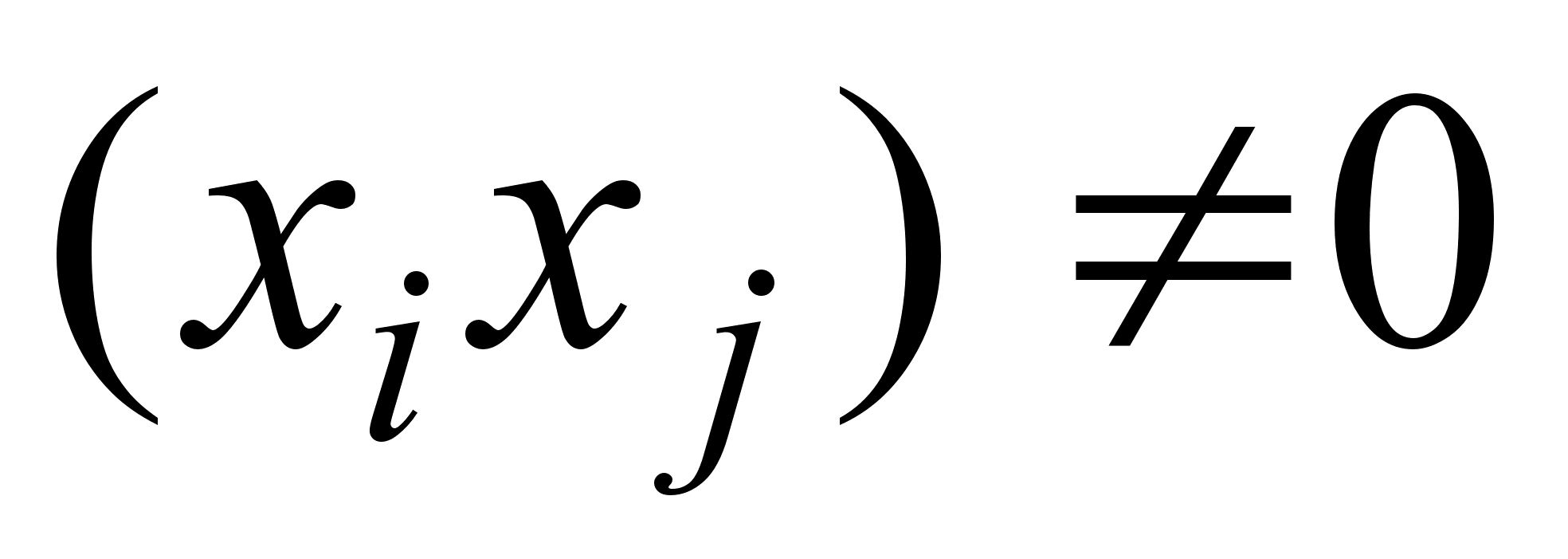 .
.
Рассчитывается статистика 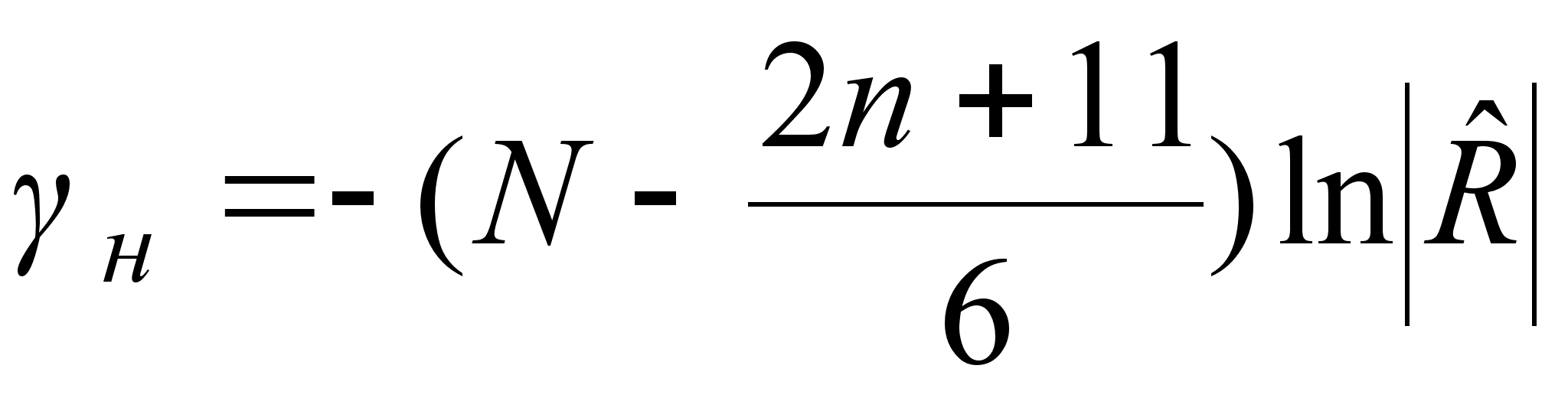 , которая распределяется по закону
, которая распределяется по закону 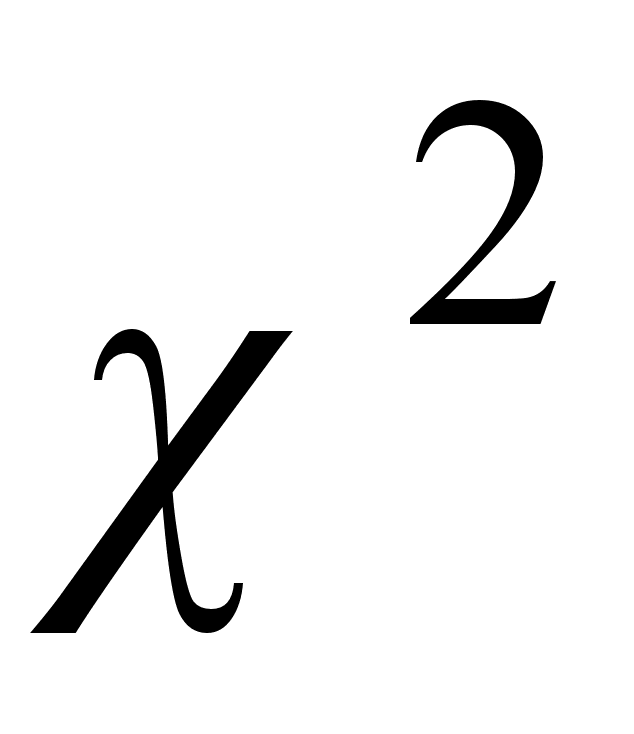 с
с 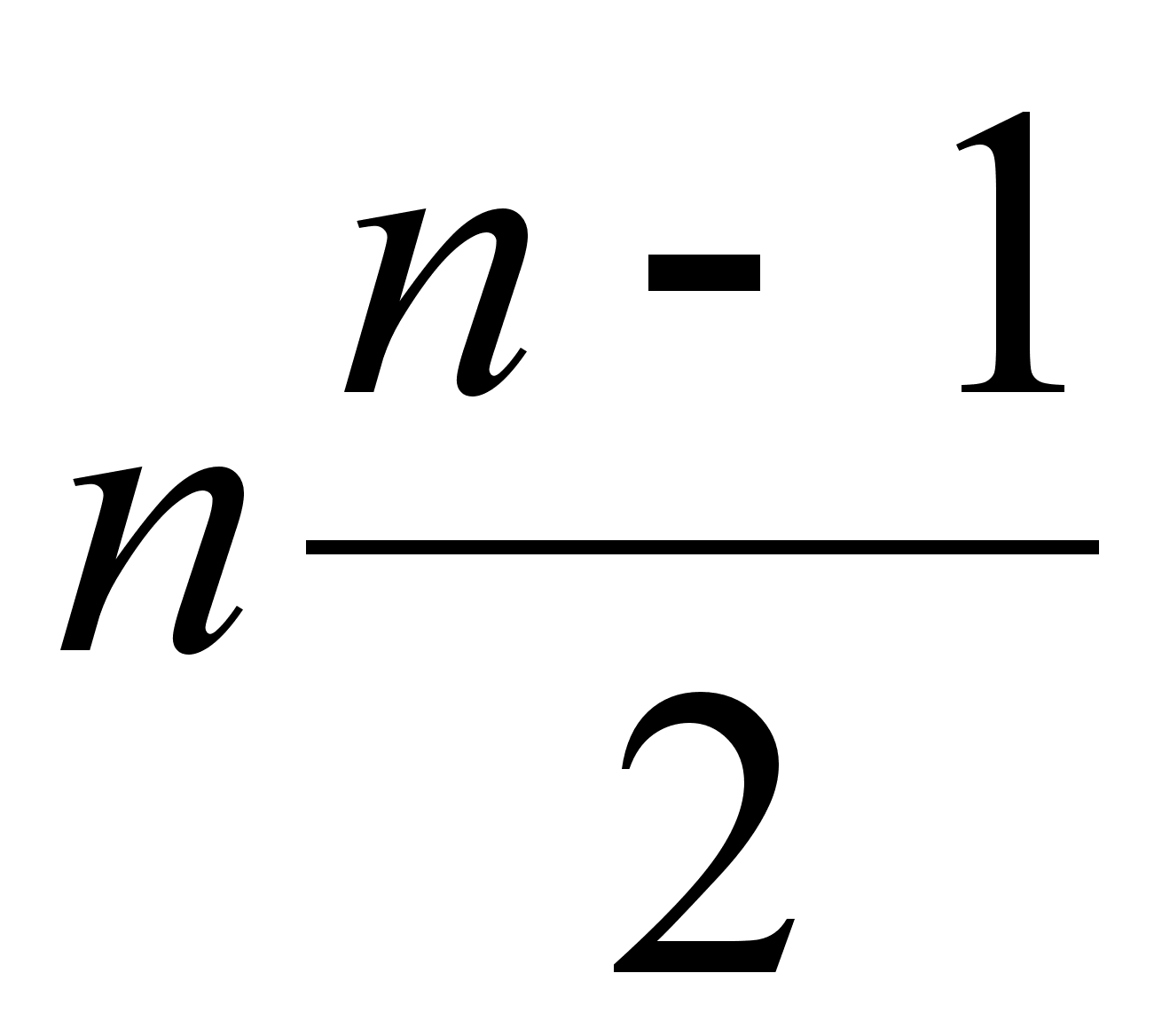 степенями свободы.
степенями свободы.
Если расчетное значения критерия будет больше табличного значения
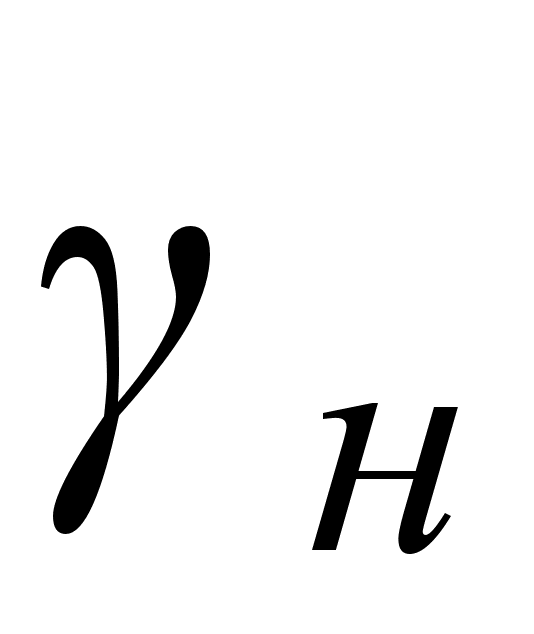 >
> 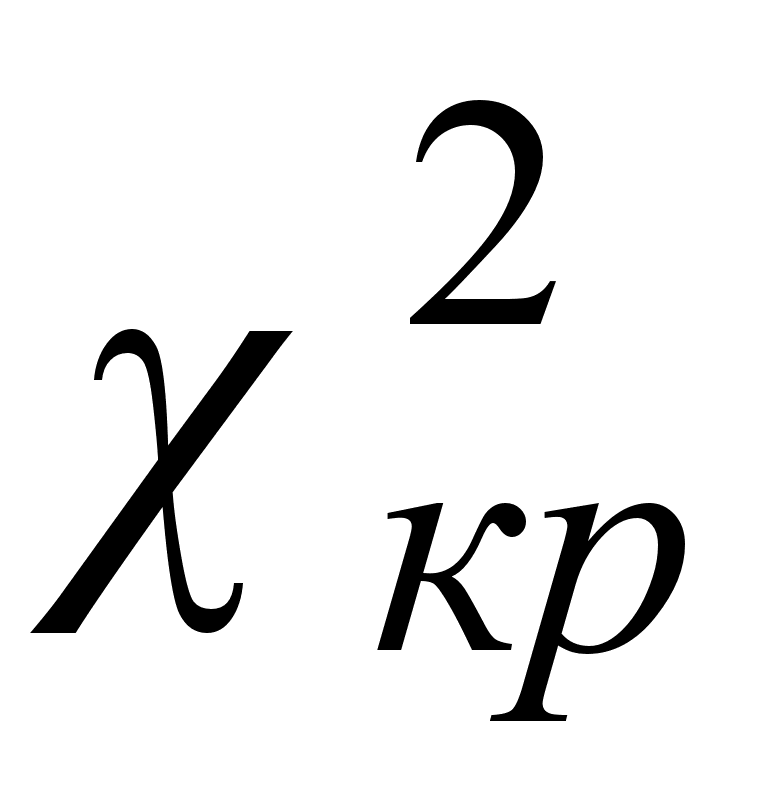 , то гипотеза Н 0 отвергается и принимается альтернативная Н 1:
, то гипотеза Н 0 отвергается и принимается альтернативная Н 1: 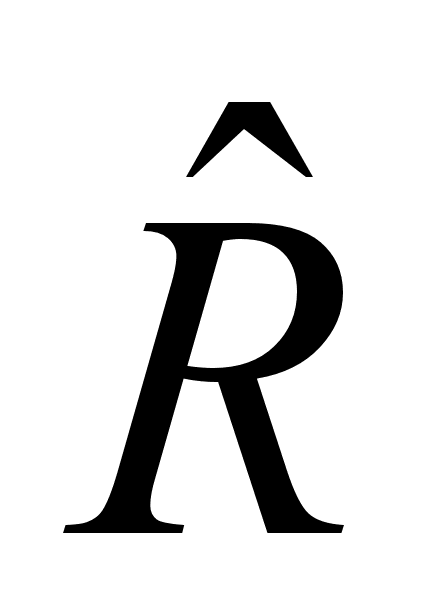 значима, что подтверждает мультиколлениарность данных, следовательно имеет смысл проводить компонентный анализ.
значима, что подтверждает мультиколлениарность данных, следовательно имеет смысл проводить компонентный анализ.
Анализ данных (табл.5) выявил значимую коррелированность переменных x 1 – x 3, что подтверждает целесообразность проведения компонентного анализа.
Компонентный анализ проводим с использованием ППП Statgraphics Plus. Для получения данных компонентного анализа вызываем подменю Tabular options ипомечаем окно Analysis Summaru. Результаты анализа приведены в таблице 6.
| Principal Components Analysis
--------------------------------------------------
Component Percent of Cumulative
Number Eigenvalue Variance Percentage
1 2,888 96,26 96,26
2 0,0985 3,28 99,54
3 0,0137 0,45 100,00
--------------------------------------------------
|
Таблица 6- Главные компоненты
На уровне информативности 95% и выше выделяется одна главная компонента. Она имеет наибольшую дисперсию, равную 96,26%. Использование второй главной компоненты не приводит к существенному увеличению дисперсии (всего на 3,28%).
Программа рассчитывает значения главных компонент для всех опытных данных. Используя значения главных компонент строим регрессионное уравнение:
Первая главная компонента z 1 адекватно описывает зависимую переменную y. Коэффициент детерминации равен R 2 = 89,34%, статистически значим при уровне значимости 0,05. Стандартная ошибка модели равна 1,25.
Факторный анализ
Факторный анализ служит для выявления и обоснования действия различных признаков и их комбинаций на исследуемый процесс путем снижения их размерности [5]. Такая задача решается, как правило, путем "сжатия" исходной информации и выделения из нее наиболее "существенной" информации. Объект описывается меньшим числом обобщенных признаков, называемых факторами.
При использовании методов факторного анализа решаются следующие задачи:
- отыскание скрытых, но объективно существующих закономерностей исследуемого процесса, определяемых воздействием внутренних и внешних причин;
- описание изучаемого процесса значительно меньшим числом факторов по сравнению с первоначально взятым количеством признаков;
- выявление первоначальных признаков, наиболее тесно связанных с основными факторами;
- прогнозирование процесса на основе уравнения регрессии, построенного по полученным факторам.
Несколько иначе осуществляется исследование латентных переменных в случае применения факторного анализа. Здесь каждая реальная переменная рассматривается также как линейная комбинация ряда факторов Fj, но в несколько необычной форме:
X i = S B ji · Fj + D i.
причем суммирование ведется по j =1… m, т.е. по каждому фактору.
Здесь коэффициент Bji принято называть нагрузкой на j- й фактор со стороны i -й переменной, а последнее слагаемое D i рассматривать как помеху, случайное отклонение для Xi. Число факторов m вполне может быть меньше числа реальных переменных n и ситуации, когда мы хотим оценить влияние всего одного фактора (ту же вежливость продавцов), здесь вполне допустимы.
Обратим внимание на само понятие “латентный”, скрытый, непосредственно не измеримый фактор. Конечно же, нет прибора и нет эталона вежливости, образованности, выносливости и т.п. Но это не мешает нам самим “измерить” их — применив соответствующую шкалу для таких признаков, разработав тесты для оценки таких свойств по этой шкале и применив эти тесты к тем же продавцам.
Так в чем же тогда “ненаблюдаемость”? А в том, что в процессе эксперимента (обязательно) массового мы не можем непрерывно сравнивать все эти признаки с эталонами. Нам приходится брать предварительные, усредненные, полученные совсем не в “рабочих” условиях данные.
Можно отойти от экономики и обратиться к спорту. Кто будет спорить, что результат спортсмена при прыжках в высоту зависит от фактора — “сила толчковой ноги”. Да, это фактор можно измерить и в обычных физических единицах (ньютонах или бытовых килограммах), но когда?! Не во время же прыжка на соревнованиях!
А ведь именно в это, рабочее время фиксируются статистические данные, накапливается материал для исходной матрицы.
Несколько более сложно объяснить сущность самих процедур факторного анализа простыми, элементарными понятиями (по мнению некоторых специалистов в области факторного анализа — вообще невозможно). Поэтому постараемся разобраться в этом, используя достаточно сложный, но, к счастью, доведенный в практическом смысле до полного совершенства, аппарат векторной или матричной алгебры.
До того как станет понятной необходимость в таком аппарате, рассмотрим так называемую основную теорему факторного анализа. Суть ее основана на представлении модели факторного анализа в матричном виде:
X [ k ·1] = B [ k·m ] · F [ m· 1] + D [ k· 1]
и на последующем доказательстве истинности выражения
R [ k·k ] = B [ k·m ] · B т[ m·k ],
для “идеального” случая, когда невязки Dпренебрежимо малы.
Здесь B т[ m·k ]это та же матрица B [ k·m ], но преобразованная особым образом (транспонированная).
Трудность задачи отыскания матрицы нагрузок на факторы очевидна — еще в школьной алгебре указывается на бесчисленное множество решений системы уравнений, если число уравнений больше числа неизвестных. Грубый подсчет говорит, что нам понадобится найти k·m неизвестных элементов матрицы нагрузок, в то время как известно около k 2 / 2 коэффициентов корреляции. Некоторую “помощь” оказывает доказанное в теории факторного анализа соотношение между данным коэффициентом парной корреляции (например, R 12) и набором соответствующих нагрузок факторов:
R 12 = B 11 · B 21 + B 12 · B 22 + … + B 1 m · B 2 m .
Таким образом, нет ничего удивительного в том утверждении, что факторный анализ (а, значит, и системный анализ в современных условиях) — больше искусство, чем наука. Здесь менее важно владеть “навыками” и крайне важно понимать как мощность, так и ограниченные возможности этого метода.
Есть и еще одно обстоятельство, затрудняющее профессиональную подготовку в области факторного анализа — необходимость быть профессионалом в “технологическом” плане, в нашем случае в предметной области.
Но, с другой стороны, стать профессионалом высокого уровня вряд ли возможно, не имея хотя бы представлений о возможностях анализировать и эффективно управлять системами на базе решений, найденных с помощью факторного анализа.
Не следует обольщаться обещаниями популяризаторов факторного анализа, не следует верить мифам о его всемогущности и универсальности. Этот метод “на вершине” только по одному показателю — своей сложности, как по сущности, так и по сложности практической реализации даже при “повальном” использовании компьютерных программ.
Контрольные вопросы
1. Какие подходы Вы знаете к решению задач, в которых используются статистические данные?
2. Что показывает матрица ковариации и в каком анализе она используется?
3. Что показывает матрица корреляции и в каком анализе она используется?
4. В чем заключается идея метода компонентного анализа?
5. Когда имеет смысл проводить компонентный анализ?
6. Для чего служит факторный анализ?
7. В чем заключается идея метода факторного анализа?
Модели временных рядов
Модели, построенные по данным, характеризующим функционирование системы или процесс за ряд последовательных равноотстоящих моментов времени, называются моделями временных рядов, в дальнейшем-временными рядами. Простейшей является модель аддитивного случайного процесса, имеющая вид:
Yt = Ut + Vt + et, (1)
где Ut - трендовая компонента;
Vt – сезонная компонента;
et – случайная компонента.
t – уровни наблюдения, t =1, 2, 3,….
Для построения модели (1) необходимо получить оценки каждой компоненты. Для выделения составляющих компонент пользуются процедурами фильтрации, регрессионного и корреляционного анализов.
Относительно трендовой составляющей Ut предполагают, что она представляет некоторую гладкую функцию, описываемую полиномом небольшой степени. Для этого чаще всего ис



 (1)
(1)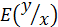 – среднее значение исследуемой величины «у» при значениях контролируемых переменных, определяемых компонентами вектора Х.
– среднее значение исследуемой величины «у» при значениях контролируемых переменных, определяемых компонентами вектора Х. – зависит от неизвестных параметров в 1, в 2, в m эта функция называется поверхностью отклика.
– зависит от неизвестных параметров в 1, в 2, в m эта функция называется поверхностью отклика.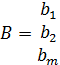 (2)
(2) (3)
(3) (4)
(4) , (5)
, (5) (6)
(6) или неизвестной поверхности
или неизвестной поверхности  в предложении справедливости (4) мы будем называть регрессионными. Процедура поиска оценок называется регрессионным анализом.
в предложении справедливости (4) мы будем называть регрессионными. Процедура поиска оценок называется регрессионным анализом. (7)
(7) состоятельные, если они сходятся по вероятности к истинным значениям параметров:
состоятельные, если они сходятся по вероятности к истинным значениям параметров: (8)
(8) – любое наперед заданное положительное число.
– любое наперед заданное положительное число. - эффективны, если имеет место неравенство:
- эффективны, если имеет место неравенство: (9)
(9)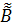 .
. есть вектор
есть вектор ,
, – обозначение градиента,
– обозначение градиента,  – частная производная функции по i -му фактору, i, j, k – единичные векторы в направлении координатных осей.
– частная производная функции по i -му фактору, i, j, k – единичные векторы в направлении координатных осей. при ограничениях, накладываемых другой функцией y2=φ2=(x1, x2,..xk) [2].
при ограничениях, накладываемых другой функцией y2=φ2=(x1, x2,..xk) [2].




 – давление,
– давление, 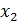 – температура химического процесса.
– температура химического процесса.
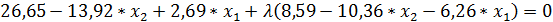
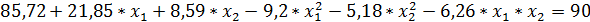




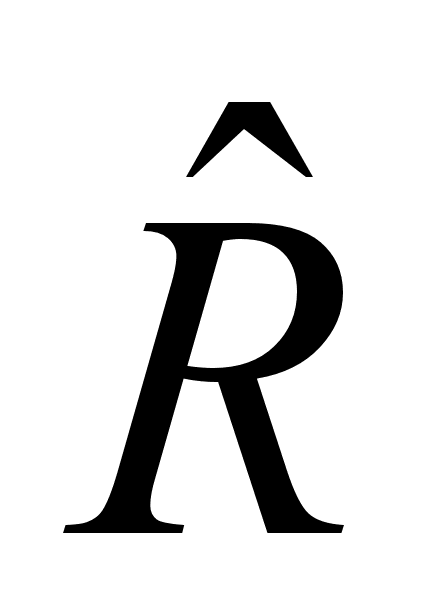 незначима и альтернативная Н 1:
незначима и альтернативная Н 1: 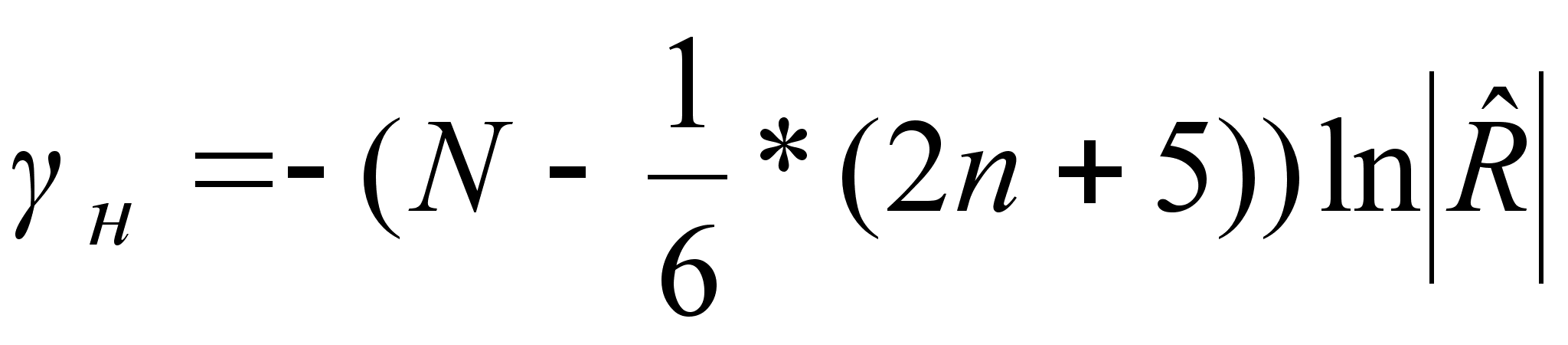
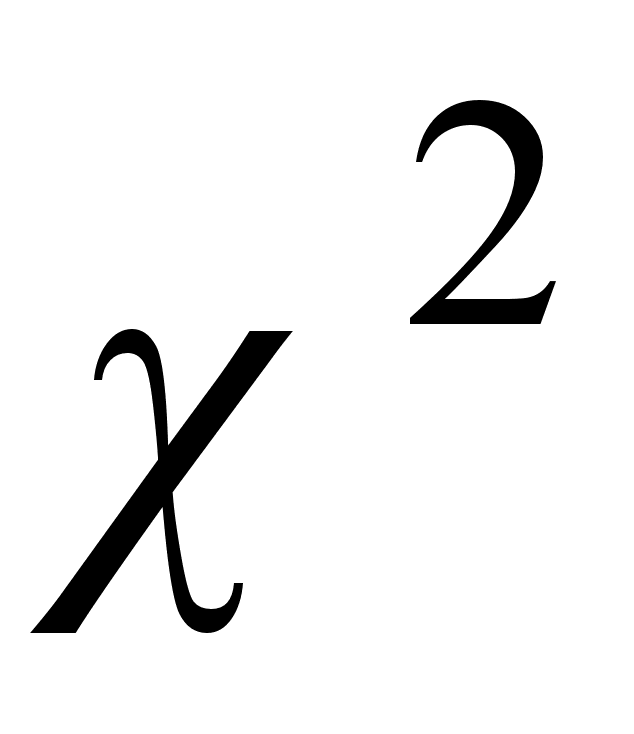 с
с 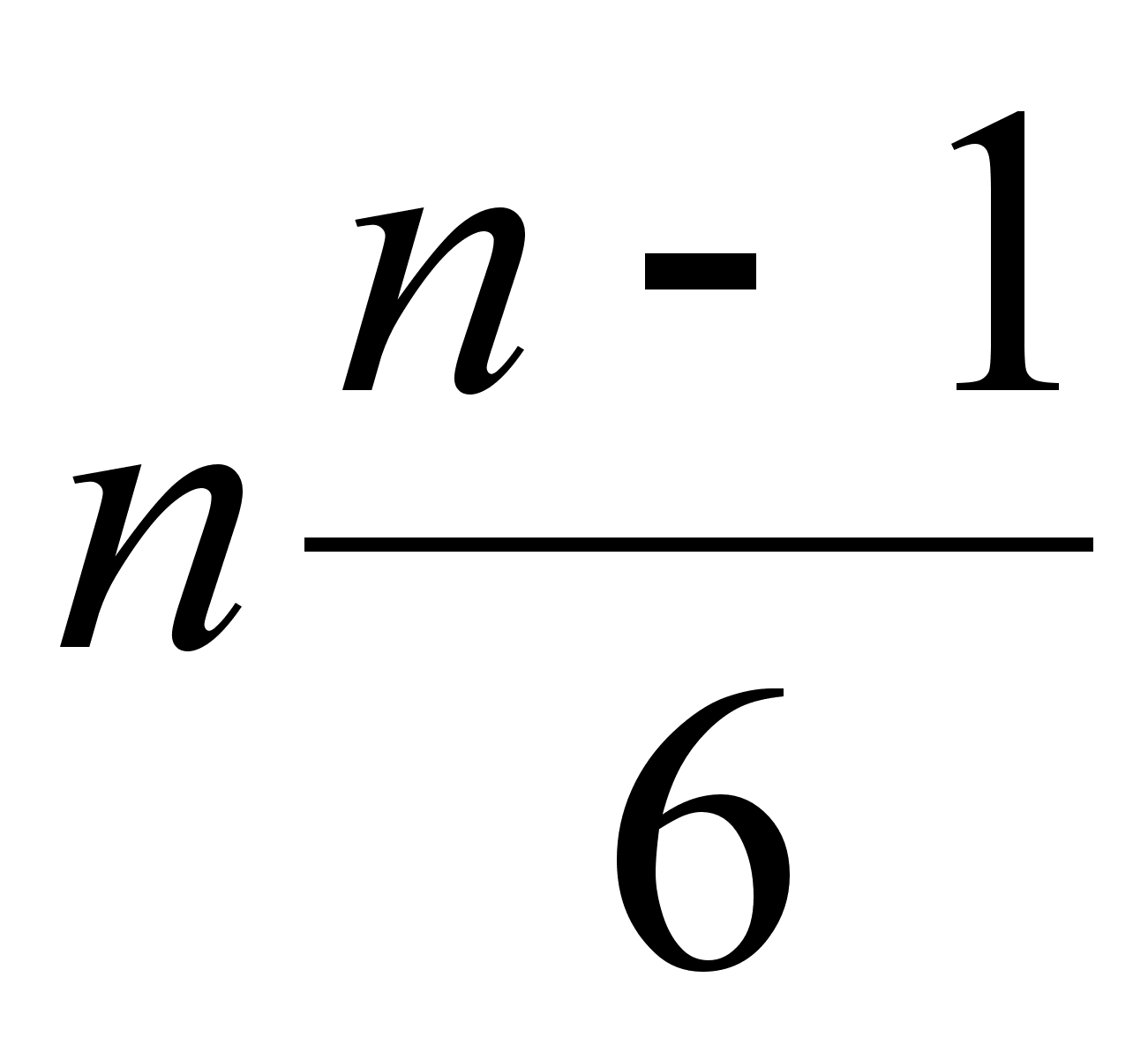 - степенями свободы. Сравнивается расчетное значение с табличным значением
- степенями свободы. Сравнивается расчетное значение с табличным значением 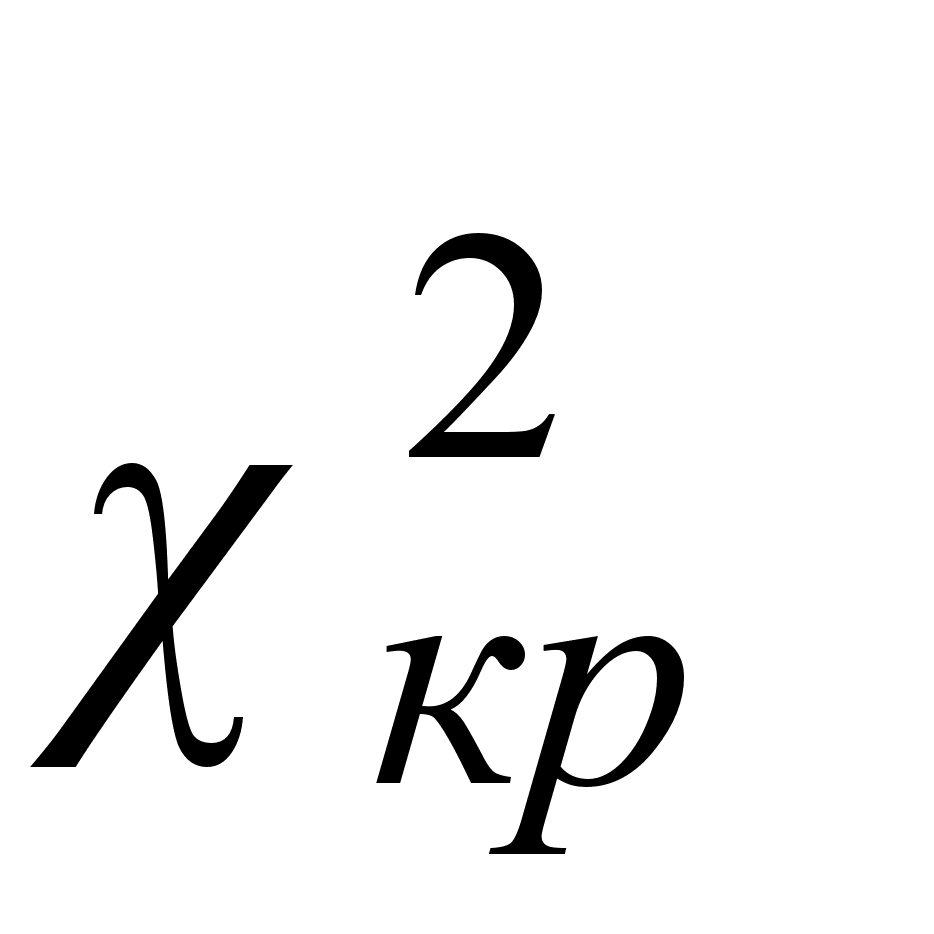 для уровня значимости α = 0,05.
для уровня значимости α = 0,05.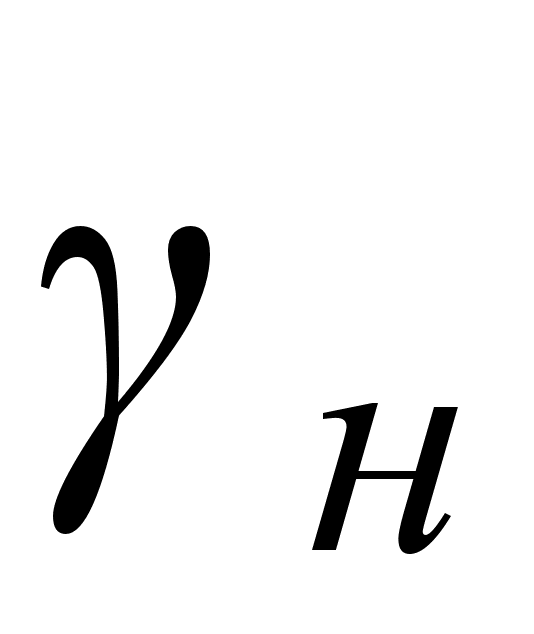 >
> 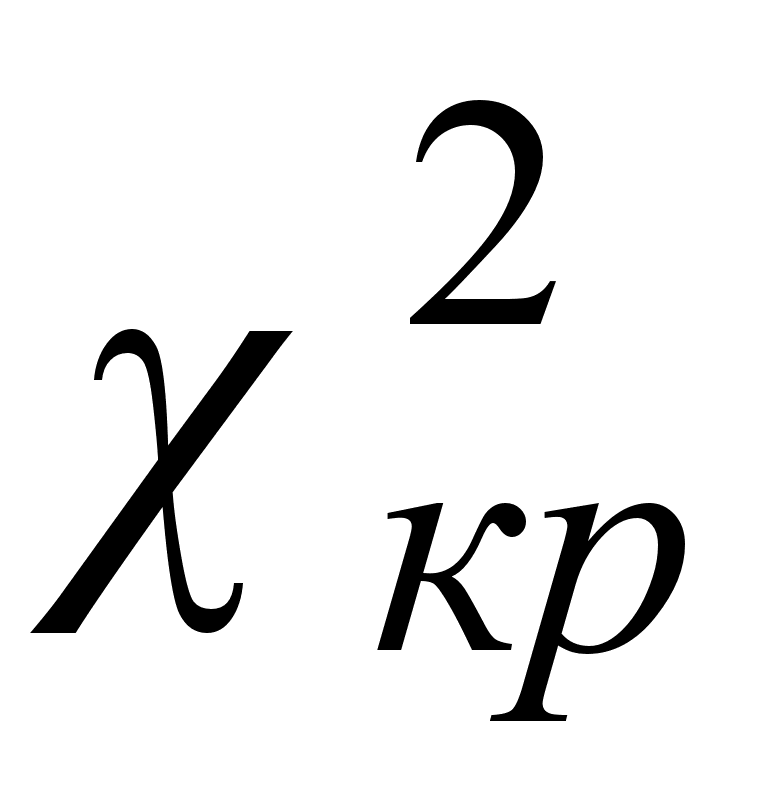 , то гипотеза Н 0 отвергается и принимается альтернативная Н 1:
, то гипотеза Н 0 отвергается и принимается альтернативная Н 1: 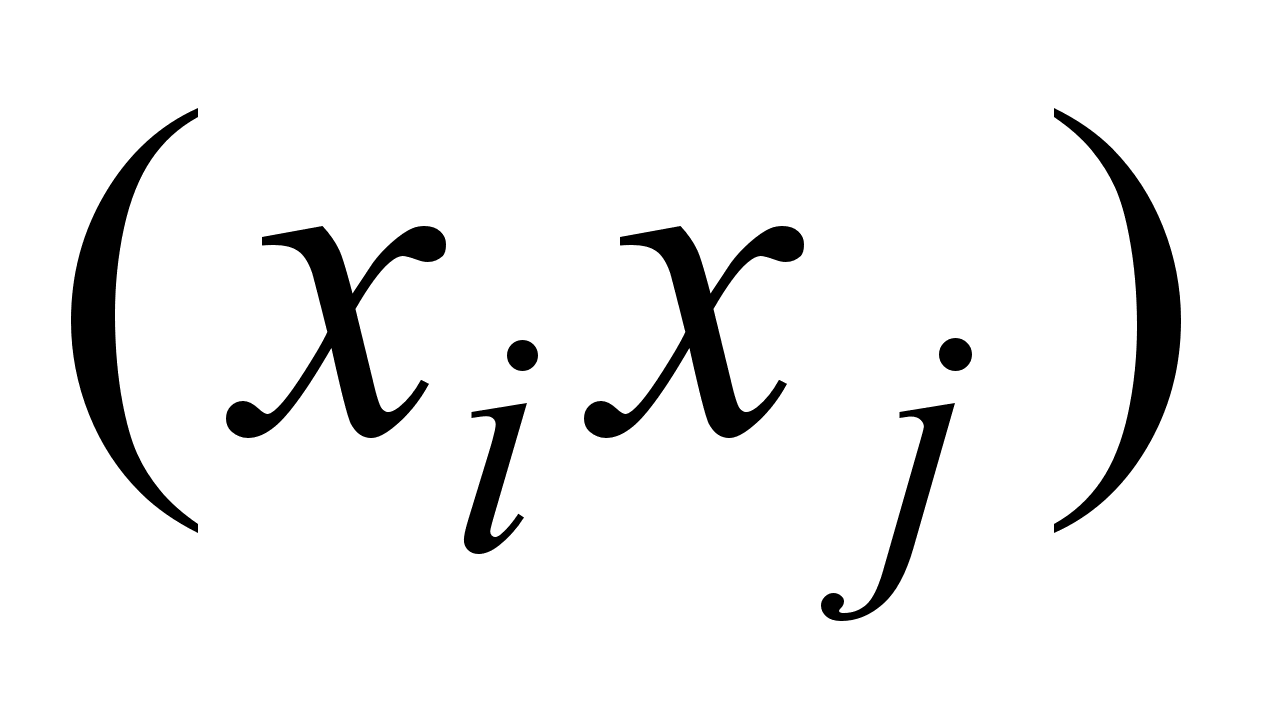 =0,
=0, 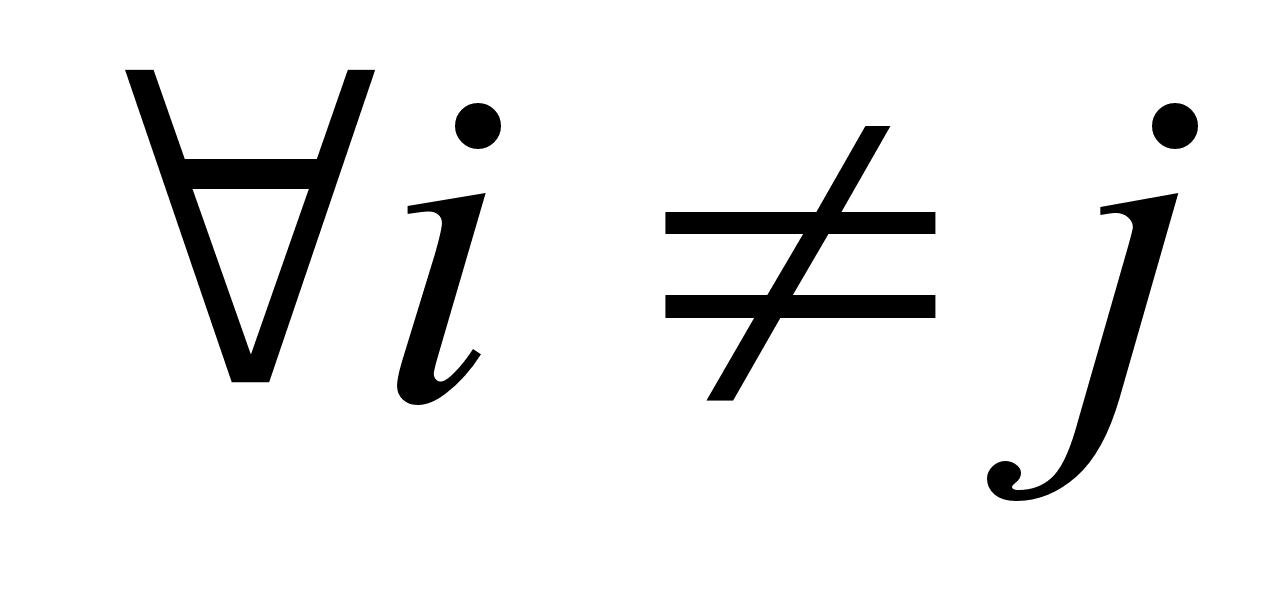 и альтернативная Н 1: соv
и альтернативная Н 1: соv 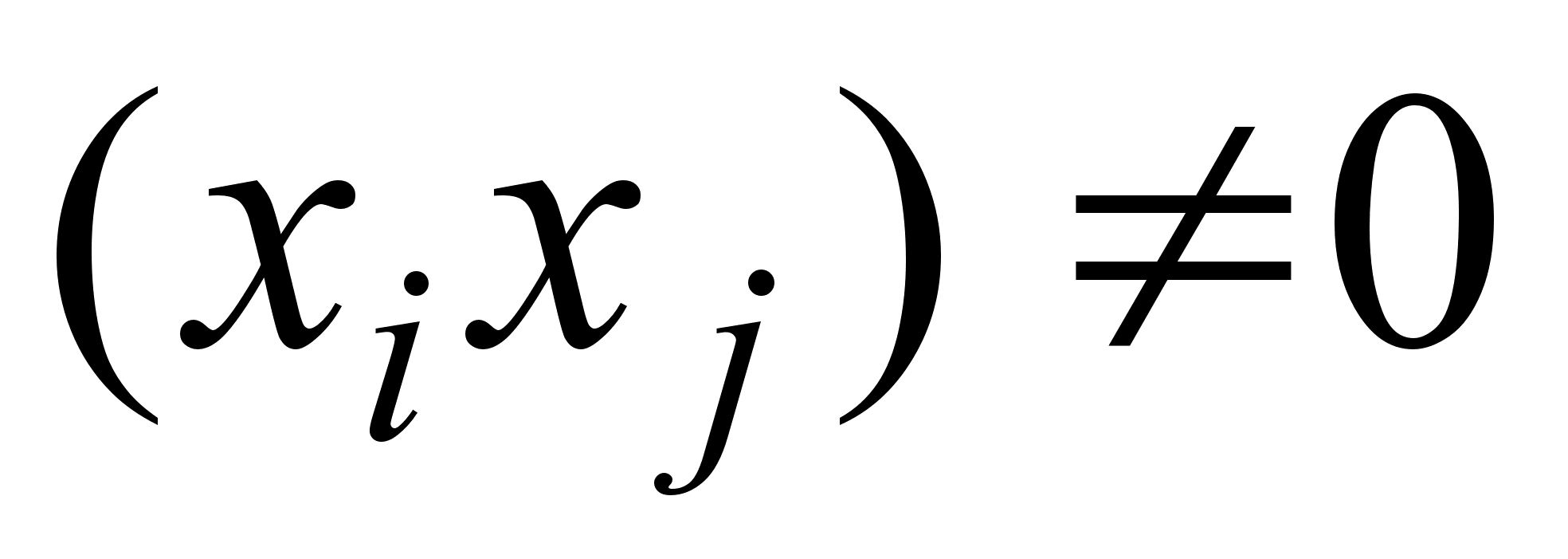 .
.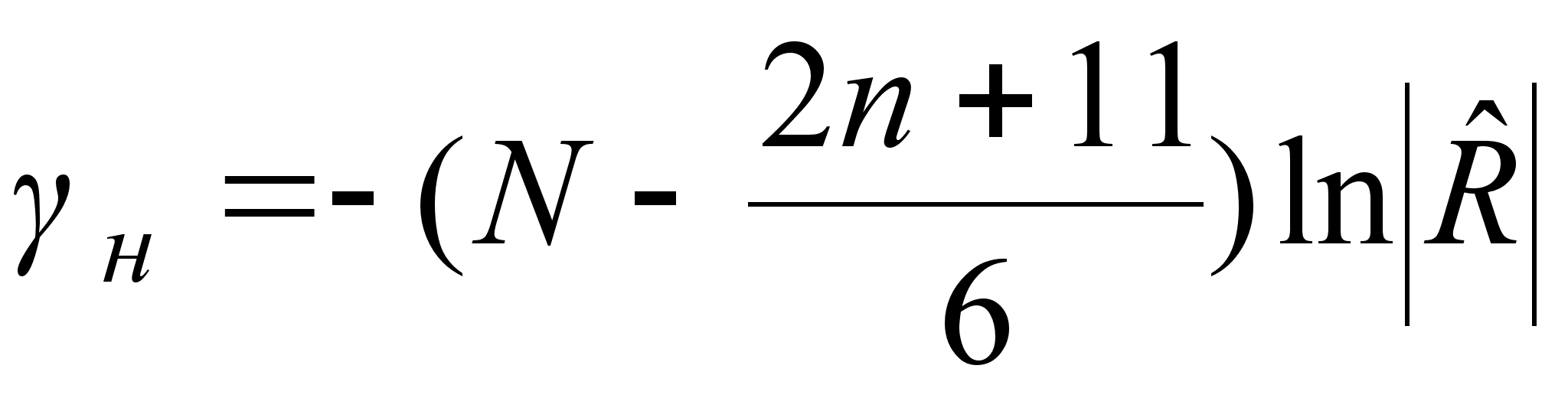 , которая распределяется по закону
, которая распределяется по закону 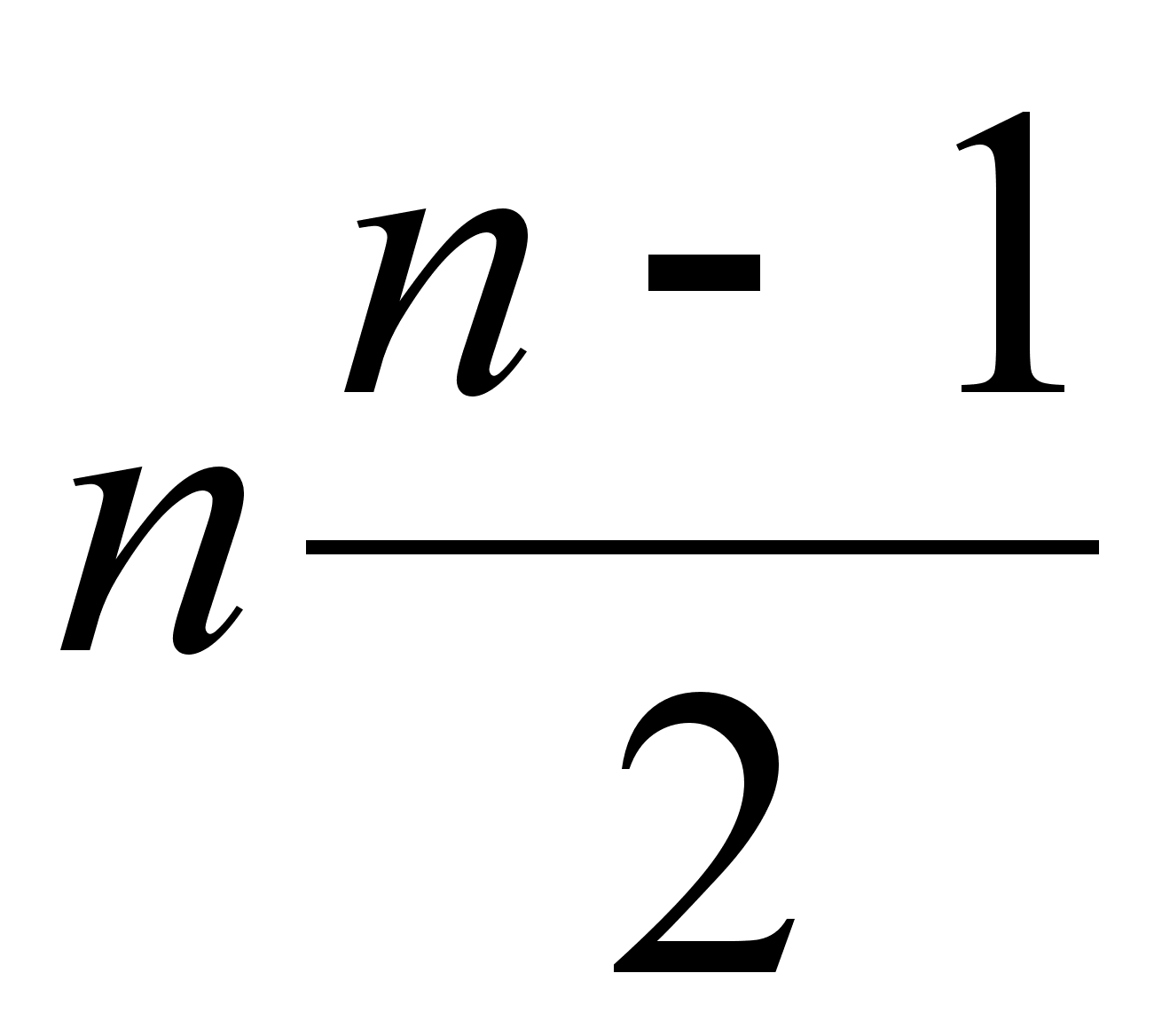 степенями свободы.
степенями свободы.


