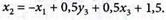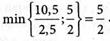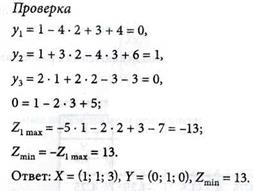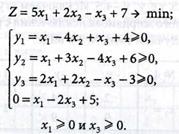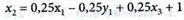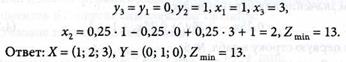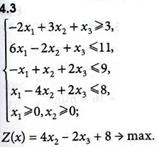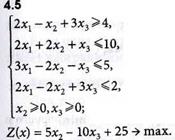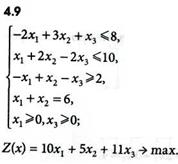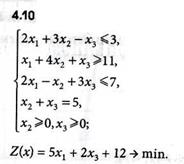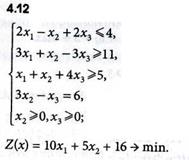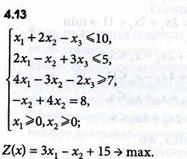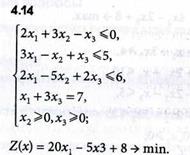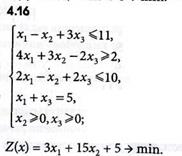Задачу о минимизации целевой функции можно решать двумя способами: 1. Задачу линейного программирования по определению минимального
значения целевой функции сводим к задаче максимизации заменой

при неизменных ограничениях, затем после решения задачи переходим к функции Zmin = -Zx max.
2. Непосредственное решение задачи минимизации целевой функции симплексным методом, при этом признаком оптимальности является условие отсутствия положительных коэффициентов в Z-строке и величина Zmin равна значению свободного члена в симплекс-таблице. Разрешающий элемент теперь следует брать в столбце над положительным коэффициентом Z-строки, а разрешающая строка выбирается из условия минимального отношения свободных членов к соответствующим коэффициентам этого столбца.
Пример 4.11
Определить минимальное значение целевой функции
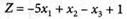 (4.60)
(4.60)
при линейных ограничениях-неравенствах
 (4.61)
(4.61)
и условиях
(4.62)
Решение
1. Целевую функцию (4.60) заменой Z1 = -Z сведем к определению максимального значения, т.е.

(4.63)
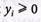 2. Введем зависимые переменные согласно условиям и запишем ограничения (4.61) в виде:
2. Введем зависимые переменные согласно условиям и запишем ограничения (4.61) в виде:
 (4.64)
(4.64)
3. Составим симплексную табл. № 1, включая в нее независимые хк, зависимые переменные уi (4.64) и целевую функцию Z1 (4.64), т.е. условие исходной задачи запишем в табл. № 1:
Первоначальный план (решение) при
х1=, х2 = х3 = 0 имеет значение
y1 = 8, y2 = 3, у3 = 5, y4 = 4 и
Z1 = -1 не является опорным, так как
y2 = -3<0.
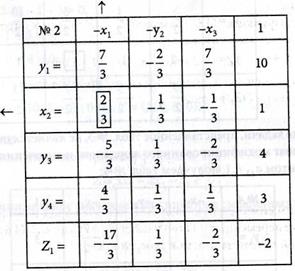
4. Определяем опорное решение задачи, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а22 = -3. В качестве разрешающего столбца выбираем столбец с переменной х2 (во второй строке с отрицательным свободным членом равным -3 отыскиваем отрицательный наибольший по модулю коэффициент, равный -3). Разрешающую строку определяем из условия:
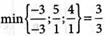
В табл. № 2 все свободные члены положительны, кроме свободного члена Z1 -строки. Следовательно, решение задачи является опорным.
5. Определяем оптимальное решение задачи, т.е. находим максимальное значение функции Z1 Так как в Z1 -строке имеется два отрицательных коэффициента -17/3 и -5/3, то в качестве разрешающего принимаем первый столбец с коэффициентом равным -17/3 (больший отрицательный по абсолютной величине). Разрешающую строку определяем из условия:
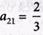

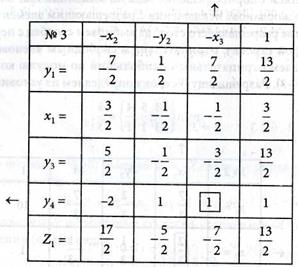
После шага модифицированного жорданова исключения с разрешающим элементом получаем табл. № 3:
Решение задачи, представленное табл. № 3, не является оптимальным. Выполняя шаг модифицированного жорданова исключения с разрешающим элементом а43 = 1, получаем табл. № 4:
Табл. № 4 заполняем в такой последовательности: выписываем разрешающие строку и столбец, а затем вычисляем значения свободных членов (столбец под 1) и коэффициентов
Z1 -строки. Так как условия опорности и оптимальности выполняются для рассматриваемой задачи, то нет необходимости в определении остальных элементов табл. № 4.
Выписываем решение задачи из табл. № 4:
Проверка

Пример 4.12
Для заданной линейной целевой функции
(4.65)
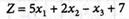
определить минимальное значение при линейных смешанных ограничениях:
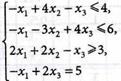 (4.66)
(4.66)
и условиях:
 (4.67)
(4.67)
Решение
1. Вводим зависимые переменные 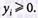 Запишем условие задачи, сведя ее к задаче максимизации, в виде:
Запишем условие задачи, сведя ее к задаче максимизации, в виде:

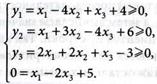 (4.68)
(4.68)
2. Составляем симплексную табл. № 1, включая в нее зависимые, независимые переменные и целевую функцию. Получаем табл. № 1 в виде:
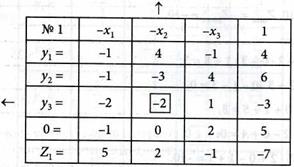
3. Исключаем свободную переменную х2, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а32 = -2. Получаем табл. № 2 в виде:

Выпишем значение для переменной х2 из табл. № 2:
(4.69)
Вычеркнем третью строку в этой таблице.
4. Исключаем 0-строку, выбирая в качестве разрешающего, столбец с положительным коэффициентом, равным 2, в этой строке, а разрешающую строку определим из условия:
После шага модифицированного жорданова исключения с разрешающим элементом
a43 = 2 получим табл. № 3:

5. В табл. № 3 вычеркиваем 0-столбец. Полученное решение не является опорным, так как в столбце свободных членов имеется отрицательное число, равное -4,5, т.е. у1 = -4,5. Исключаем эту величину, сделав шаг модифицированного жорданова исключения с разрешающим элементом а11 = -4,5. Получаем табл. № 4 в виде:
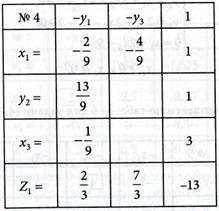
Из табл. № 4 выписываем решение задачи, а значение х2 вычисляем на основании (4.69):

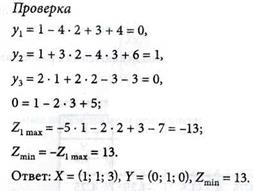
6. Решим задачу минимизации непосредственно (на примере 4.12), определяя значение целевой функции методом модифицированных жордановых исключений. Условием оптимальности при минимизации целевой функции является отсутствие положительных коэффициентов в Z-строке симплексной таблицы. Условие задачи запишем в виде:
(4.70)
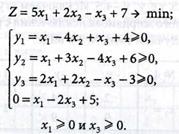
(4.71)
Решение
7. Составляем симплексную табл. № 5 для задачи (4.70) и (4.71) в виде:

8. Исключаем свободную переменную х2 в табл. № 5, сделав шаг модифицированного жорданова исключения с разрешающим элементом а12 = 4. Получим табл. № 6 в виде:
(4.72)
Выпишем значение для переменной
х2
и вычеркнем первую строку в табл. № 6.
9. Исключаем 0-строку, выполнив шаг модифицированного жорданова исключения с разрешающим элементом а43 = 2. Получим табл. № 7 в виде:

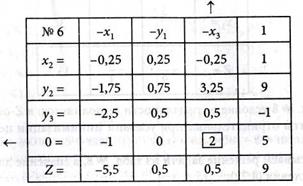
10. В табл. № 7 вычеркиваем 0-столбец и исключаем отрицательный свободный член, т.е. определяем опорное решение, с разрешающим элементом a21 = -2,25, Получаем табл. № 8 в виде:


В табл. № 8 условие оптимальности выполняется: в Z-строке все коэффициенты отрицательные при условии минимизации целевой функции Z.
Выписываем решение задачи из табл. № 8, а значение для х2 определяем из условия (4.72):
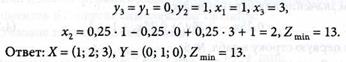
Контрольные вопросы
1. В чем заключается сущность симплексного метода решения задач линейного программирования?
2. Как составляются симплексные таблицы?
3. Решение задач линейного программирования способом модифицированных жордановых исключений.
4. Сформулируйте признаки опорности и оптимальности решения задач линейного программирования.
5. Как определяются разрешающие элементы при определении опорного и оптимального решений задачи линейного программирования?
6. Укажите последовательность решения задач линейного программирования при смешанных ограничениях и наличии свободных независимых переменных.
7. Какими способами решаются задачи линейного программирования при минимизации целевой функции?
8. Назовите условие несовместности системы ограничений и признак неограниченности целевой функции в задачах линейного программирования.
9. По какому правилу выбираются разрешающие элементы при исключении свободных независимых переменных и 0-строк в симплексных таблицах?
Задачи 4.1-4.16


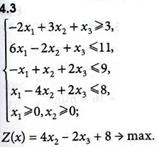


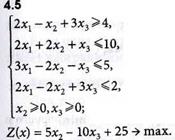


Определить оптимальные решения задач линейного программирования симплексным методом
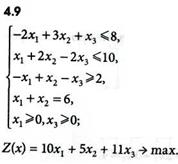
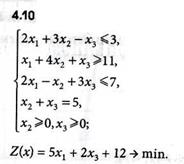

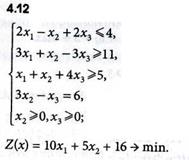
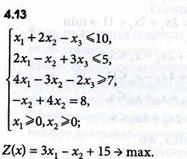
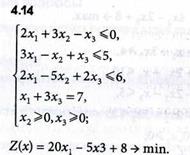
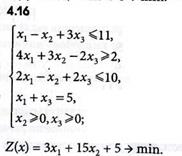






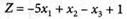 (4.60)
(4.60) (4.61)
(4.61)

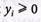 2. Введем зависимые переменные согласно условиям и запишем ограничения (4.61) в виде:
2. Введем зависимые переменные согласно условиям и запишем ограничения (4.61) в виде: (4.64)
(4.64)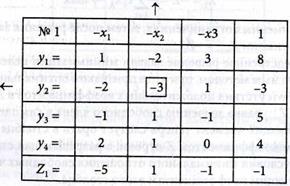
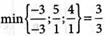
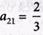




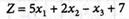
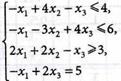 (4.66)
(4.66) (4.67)
(4.67)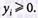 Запишем условие задачи, сведя ее к задаче максимизации, в виде:
Запишем условие задачи, сведя ее к задаче максимизации, в виде:
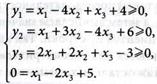 (4.68)
(4.68)