Понятие площади является широко известным в математике, которое также часто используют в практике. С древних времен площадь является неопределяемым понятием. Вычисляя площадь, математики не задумывались, что данное понятие нуждается в четком определении. Но часто на уроках по геометрии говорят, что площадь  фигуры
фигуры 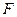 есть число, которое показывает, из скольких единиц площади составляет фигура. Данное утверждение не является определением, это всего лишь описание того, что такое площадь. Но чтобы при вычислении площади получалось определенное число, нужно основываться на каких-нибудь принципах, и такие принципы в математике существуют. Они сформулированы следующим образом:
есть число, которое показывает, из скольких единиц площади составляет фигура. Данное утверждение не является определением, это всего лишь описание того, что такое площадь. Но чтобы при вычислении площади получалось определенное число, нужно основываться на каких-нибудь принципах, и такие принципы в математике существуют. Они сформулированы следующим образом:
1. Положительность. Площадь фигуры есть неотрицательное число.
2. Аддитивность. Площадь фигуры, составленной из нескольких фигур без общих внутренних точек, равна сумме площадей этих фигур.
3. Инвариантность. Равные фигуры имеют равные площади.
4. Нормированность. Площадь единичного квадрата равна единице.
Данные свойства были не единственными, которыми математики пользовались при вычислении площади фигур. Остальные свойства оказались следствиями этих четырех. Например, следствием положительности и аддитивности площадей является монотонность: площадь части фигуры не превышает площади всей фигуры.
Пусть F - фигура, площадь которой нужно вычислить. Обозначим площадь фигуры через S. Рассмотрим всевозможные многоугольные фигуры, содержащиеся в F и всевозможные многоугольные фигуры, содержащие F. Фигуры, содержащиеся в F, называются входящими в F, а содержащие F – объемлющими. В силу монотонности площади, для любой входящей многоугольной фигуры Р и любой объемлющей фигуры Q справедливо неравенство (1.1)
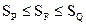 (1.1)
(1.1)
Площади фигур Р и Q есть приближенные значения площади фигуры F с недостатком и с избытком. Погрешности обоих приближений, т.е. разности  и
и  , не превышают разности
, не превышают разности 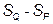 . Допустим, что путем надлежащего выбора многоугольных фигур P и Q можно сделать последнюю разность сколь угодно малой. Значит и погрешности приближений могут быть сделаны сколь угодно малыми. Это значит, что площадь фигуры F может быть вычислена с произвольной степенью точности.
. Допустим, что путем надлежащего выбора многоугольных фигур P и Q можно сделать последнюю разность сколь угодно малой. Значит и погрешности приближений могут быть сделаны сколь угодно малыми. Это значит, что площадь фигуры F может быть вычислена с произвольной степенью точности.
Данный метод применим только к фигурам F, для которых существуют входящие многоугольные фигуры P и объемлющие многоугольные фигуры Q, со сколь угодно малыми разностями 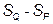 . Такие фигуры называются квадрируемыми.
. Такие фигуры называются квадрируемыми.
Из вышесказанного следуют три положения:
1) Каждой квадрируемой фигуре отвечает определенное число – ее площадь.
2) Данные числа - площади обладают свойствами 1-4.
3) Площадь любой квадрируемой фигуры можно вычислить с произвольной степенью точности на основании свойств 1-4.
Таким образом, площадь может быть определена как функция квадрируемой фигуры, обладающая свойствами 1-4.
Чтобы дать полное определение площади, необходимо определить площадь на классе многоугольных фигур с помощью тех же условий 1 - 4. Таким образом, полная формулировка определения площади состоит из трех частей:
1) площадь определяется как функция со свойствами 1 - 4 на классе многоугольных фигур;
2) определяется класс квадрируемых фигур;
3) площадь определяется как функция со свойствами 1- 4 на классе квадрируемых фигур
Данное определение называется аксиоматическим определением площади.
Ломаной линией называется конечная последовательность отрезков, такая, что один из концов первого отрезка служит концом второго, другой конец служит концом третьего и т.д., при этом соседние отрезки не лежат на одной прямой. На рис. 1.1 представлен пример ломаной.

Рис. 1.1. Ломаная

Простая замкнутая ломаная вместе с частью плоскости, ограниченной ею, называется многоугольником. Простой многоугольной фигурой называется конечная часть плоскости, ограниченная многоугольником, который дан на рис. 1.2.
Рис. 1.2. Многоугольник
Величина части плоскости, заключенной внутри многоугольника, называется площадью многоугольника. Соотношение между площадями фигур и числами, их измеряющими, должно удовлетворять следующим условиям:
1.Числа, измеряющие площади двух равных фигур, должны быть равны между собой;
2. Если данная фигура разбита на несколько частей, составляющих каждая замкнутую фигуру, то число, измеряющее площадь всей фигуры, должно быть равно сумме чисел, измеряющих площади отдельных ее частей.
3. Площадь квадрата, со стороной, равной единице измерения, равна единице.
Фигуры, которые имеют равные площади, называют равновеликими. Равные фигуры (которые совмещаются при наложении) всегда являются равновеликими, однако равновеликие фигуры могут быть неравными (рис. 1.3)

Рис. 1.3. Неравные равновеликие фигуры
4. Фигуры также являются равновеликими, если они могут быть дополнены равными (или равновеликими) фигурами так, что образуются одинаковые суммы, или суммы, равные между собой.
 Рассмотрим параллелограммы ABCD и AEFD, которые представлены на рис. 1.4.
Рассмотрим параллелограммы ABCD и AEFD, которые представлены на рис. 1.4.
Рис. 1.4. Параллелограммы
Данные параллелограммы построены на одном основании AD и имеют одинаковые высоты. Дополним параллелограмм ABCD треугольником DCF, а параллелограмм AEFD – треугольником АВЕ. Получим одну и ту же сумму – трапецию ABFD. Дополняющие треугольники равны между собой и после дополнения получилась одна и та же сумма, следовательно, параллелограммы ABCD и AEFD являются равновеликими.
5.Площадь одной фигуры считается меньше площади другой фигуры, если первая окажется равновеликой какой-нибудь части другой.

Площадь треугольника АВС, который представлен на рис. 1.5,состоящего из двух прямоугольных треугольников 1 и 2, меньше площади трапеции DEFG, состоящей из двух таких же треугольников и из третьего треугольника.
Рис. 1.5. Сравнение площадей треугольника АВС и трапеции DEFG
Равновеликость, указанная в условии 2 называют равновеликостью по разложению, а равновеликость, указанную в условии 4 – равновеликостью по дополнению.
Равновеликость второго рода всегда может быть сведена на равновеликость первого рода, т.е. всякие две фигуры, равновеликие по дополнению, могут быть разложены на одинаковое число частей, соответственно совмещающихся.
Для измерения площади фигуры выбирают некоторый многоугольник, площадь которого принимают за единицу площади; мерой какой-либо площади будет отношение этой площади к единице площади.
Единицей измерения площади принято считать площадь квадрата, сторона которого равна линейной единице (1 метр, 1 сантиметр и т.д.). Для простейших фигур меру площади можно получить следующим образом: накладываем единицу площади на измеряемую фигуру столько раз, сколько это возможно. Допустим, что на фигуру, площадь которой надо измерить, наложена сеть квадратов. Если контур данной фигуры есть ломаная, стороны которой совпадают с частями прямых линий, образующих сеть квадратов, то число квадратов, лежащих внутри фигуры, составит точную меру измеряемой площади (рис. 1.6)

Рис. 1.6. Наложение единицы площади на измеряемую фигуру
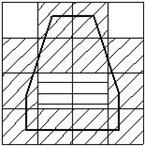
Практически площадь многоугольника можно измерить следующим образом: расчертим лист бумаги на квадраты со стороной, равной единице измерения отрезков, и наложим на него данный многоугольник. Пусть m – число квадратов, покрытых многоугольником, а n – число квадратов, покрытых многоугольником лишь частично. Данный способ представлен на рис. 1.7.
Рис.1.7.Практическое измерение площади многоугольника
Число S, выражающее площадь многоугольника, заключено между числами  :
:
 (1.2)
(1.2)
Каждое из чисел s1 и S1 может рассматриваться как приближенное значение числа S. Чтобы более точно измерить площадь данного многоугольника, разобьем каждый из n частично покрытых квадратов на 100 квадратов меньшего размера. Сторона каждого из этих квадратов равна  , площадь каждого из них равна
, площадь каждого из них равна 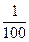 . Пусть m1 - число квадратов, полностью покрытых многоугольником, n1 – число частично покрытых квадратов. Число S заключено между числами
. Пусть m1 - число квадратов, полностью покрытых многоугольником, n1 – число частично покрытых квадратов. Число S заключено между числами  и
и  , т.е.
, т.е.
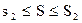 (1.3)
(1.3)
При этом очевидно
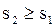 (1.4)
(1.4)
С другой стороны,
 (1.5)
(1.5)
поскольку фигура с площадью S1 содержит все квадраты меньшего размера, на которые разбиты n квадратов, а фигура с площадью S2 – только те из квадратов меньшего размера, которые полностью или частично покрыты данным многоугольником. Таким образом
 (1.6)
(1.6)
Разобьем теперь каждый из n1 частично покрытых квадратов меньшего размера на 100 еще меньших равных квадратов со стороной  и повторим рассуждения. Получим новые неравенства
и повторим рассуждения. Получим новые неравенства
 (1.7)
(1.7)
Снова повторим аналогичные рассуждения и т.д. Для любого натурально числа k получаются неравенства
 (1.8)
(1.8)
 причем разность Sk - sk при неограниченном увеличении k будет стремиться к нулю, т.к. разность Sk - sk равна площади фигуры, составленной из квадратов со стороной
причем разность Sk - sk при неограниченном увеличении k будет стремиться к нулю, т.к. разность Sk - sk равна площади фигуры, составленной из квадратов со стороной  и покрывающих ломаную, ограничивающую многоугольник (рис. 1.8.)
и покрывающих ломаную, ограничивающую многоугольник (рис. 1.8.)
Рис.1.8. Вычисление площади фигуры, составленной из квадратов
С увеличением k данная фигура все ближе и ближе «сжимается» к ломаной, и поэтому ее площадь стремится к нулю. Значит и числа sk и Sk будут стремиться к S. В этом и состоит процесс измерения площади многоугольника, который позволяет найти приближенное значение S с произвольной точностью



 фигуры
фигуры 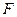 есть число, которое показывает, из скольких единиц площади составляет фигура. Данное утверждение не является определением, это всего лишь описание того, что такое площадь. Но чтобы при вычислении площади получалось определенное число, нужно основываться на каких-нибудь принципах, и такие принципы в математике существуют. Они сформулированы следующим образом:
есть число, которое показывает, из скольких единиц площади составляет фигура. Данное утверждение не является определением, это всего лишь описание того, что такое площадь. Но чтобы при вычислении площади получалось определенное число, нужно основываться на каких-нибудь принципах, и такие принципы в математике существуют. Они сформулированы следующим образом: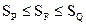 (1.1)
(1.1) и
и  , не превышают разности
, не превышают разности 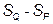 . Допустим, что путем надлежащего выбора многоугольных фигур P и Q можно сделать последнюю разность сколь угодно малой. Значит и погрешности приближений могут быть сделаны сколь угодно малыми. Это значит, что площадь фигуры F может быть вычислена с произвольной степенью точности.
. Допустим, что путем надлежащего выбора многоугольных фигур P и Q можно сделать последнюю разность сколь угодно малой. Значит и погрешности приближений могут быть сделаны сколь угодно малыми. Это значит, что площадь фигуры F может быть вычислена с произвольной степенью точности.


 Рассмотрим параллелограммы ABCD и AEFD, которые представлены на рис. 1.4.
Рассмотрим параллелограммы ABCD и AEFD, которые представлены на рис. 1.4.


 :
: (1.2)
(1.2) , площадь каждого из них равна
, площадь каждого из них равна 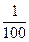 . Пусть m1 - число квадратов, полностью покрытых многоугольником, n1 – число частично покрытых квадратов. Число S заключено между числами
. Пусть m1 - число квадратов, полностью покрытых многоугольником, n1 – число частично покрытых квадратов. Число S заключено между числами  и
и  , т.е.
, т.е.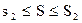 (1.3)
(1.3)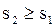 (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6) и повторим рассуждения. Получим новые неравенства
и повторим рассуждения. Получим новые неравенства (1.7)
(1.7) (1.8)
(1.8) причем разность Sk - sk при неограниченном увеличении k будет стремиться к нулю, т.к. разность Sk - sk равна площади фигуры, составленной из квадратов со стороной
причем разность Sk - sk при неограниченном увеличении k будет стремиться к нулю, т.к. разность Sk - sk равна площади фигуры, составленной из квадратов со стороной  и покрывающих ломаную, ограничивающую многоугольник (рис. 1.8.)
и покрывающих ломаную, ограничивающую многоугольник (рис. 1.8.)


