Теорема 1. Если стороны прямоугольника равны a и b, то его площадь равна произведению ab
 (1.9)
(1.9)
Доказательство:
При доказательстве возможны два случая:
1. a и b – рациональные числа;
2. a и b – произвольные.
1.Рассмотрим первый случай, когда a и b – рациональные числа.
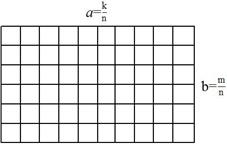
Пусть 
 (рис. 1.9.)
(рис. 1.9.)
Рис. 1.9 К доказательству теоремы 1
Разделим сторону a рассматриваемого прямоугольника на k равных частей, а сторону b – на m равных частей. Через точки деления проведем прямые, параллельные сторонам прямоугольника. Тогда весь прямоугольник окажется разделенным на km квадратов со стороной  , площади которых равны
, площади которых равны  . Таким образом, площадь прямоугольника равна
. Таким образом, площадь прямоугольника равна
 . (1.10)
. (1.10)
2. Рассмотрим случай, когда a и b – произвольные. Возьмем произвольное натуральное число n и подберем натуральные числа k и m такие, что выполняются двойные неравенства
 (1.11)
(1.11)

Рассмотрим три прямоугольника: первый – со сторонами  и
и 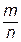 ; второй – со сторонами a и b; третий – со сторонами
; второй – со сторонами a и b; третий – со сторонами  и
и  . Их можно расположить так, что первый прямоугольник не выходит за пределы второго, а третий содержит второй. Это изображено на рис. 1.10.
. Их можно расположить так, что первый прямоугольник не выходит за пределы второго, а третий содержит второй. Это изображено на рис. 1.10.
Рис. 1.10. Иллюстрация расположения прямоугольников
Из свойств площади следует, что площадь второго прямоугольника меньше площади третьего и не меньше площади первого.
Площадь первого прямоугольника равна  , а площадь третьего составляет
, а площадь третьего составляет  .
.
Пусть S – площадь второго прямоугольника. Тогда
 (1.12)
(1.12)
Но из двойных неравенств
 (1.13)
(1.13)
следует то, что
 (1.14)
(1.14)
В левой части двойного неравенства для S заменим k и m меньшими величинами, а в правой – большими. Получим
 . (1.15)
. (1.15)
После раскрытия скобок
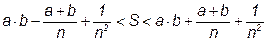 (1.16)
(1.16)
и
 . (1.17)
. (1.17)
Вычитая из всех частей неравенства  , получаем
, получаем
 , (1.18)
, (1.18)
т.е.
 (1.19)
(1.19)
Последнее неравенство верно при любом n. Но в его левой части стоит неотрицательное число, не зависящее от n. Если предположить, что  , то это число будет положительным. Выбирая теперь n достаточно большим, можно сделать правую часть неравенства меньше любого положительного числа, а значит, меньше левой его части, если
, то это число будет положительным. Выбирая теперь n достаточно большим, можно сделать правую часть неравенства меньше любого положительного числа, а значит, меньше левой его части, если  .
.
Таким образом, каковы бы ни были числа a и b  .
.
Лемма 1. Площадь прямоугольного треугольника равна половине произведения его катетов.
Доказательство.
Пусть дан прямоугольный треугольник Т с катетами a и b, который представлен на рис. 1.11.
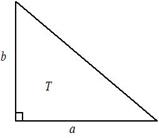
Рис. 1.11 Прямоугольный треугольник

Достроим его до прямоугольника Р со сторонами a и b, проведя через вершины его острых углов прямые, перпендикулярные катетам, как на рис. 1.12.
Рис. 1.12 Треугольник, достроенный до прямоугольника
Гипотенуза треугольника Т разбивает прямоугольник Р на два равных треугольника: треугольник Т и равный ему треугольник Т1. Поэтому
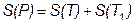
(1.20)
и
 . (1.21)
. (1.21)
Значит,
 (1.22)
(1.22)
Так как
 , (1.23)
, (1.23)
то
 (1.24)
(1.24)
Теорема 2. Площадь треугольника равна половине произведения любой из его сторон и проведенной к ней высоты.
Доказательство.
Рассмотрим треугольник АВС. Обозначим его Т. Сторону треугольника Т, противоположную вершине С, обозначим с, а опущенную из вершины С высоту обозначим hс. Докажем, что
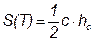 (1.25)
(1.25)
Возможны три случая расположения точки Н на АВ.
1) Точка Н совпадает с одним из концов основания с, например, с точкой А.
В этом случае высота hc совпадает со стороной СА, так что треугольник Т прямоугольный. Его катеты – отрезки СА=hс и ВА=с. По лемме 1 получаем, что
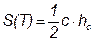 , (1.26)
, (1.26)
т.е. выполняется равенство (1.25)
2) Точка Н лежит на основании с. Это представлено на рис. 1.13.
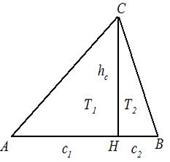
Тогда высота СН разбивает треугольник Т на два прямоугольных треугольника Т1 и Т2 с катетами с1 и с2 и общим катетом hc.
Рис.1.13. Точка Н лежит на основании треугольника
Площади треугольников Т1 и Т2 вычисляются по формулам

(1.27)
и
 . (1.28)
. (1.28)
Так как
 , (1.29)
, (1.29)
то
 , (1.30)
, (1.30)
т.е. формула (1.25) выполняется и во втором случае.
3) Точка Н лежит вне основания с, например, так, что точка В лежит между А и Н
Тогда прямоугольный треугольник  разбивается отрезком СВ на треугольник Т и прямоугольный треугольник
разбивается отрезком СВ на треугольник Т и прямоугольный треугольник  . Поэтому
. Поэтому
 . (1.31)
. (1.31)
Следовательно
 . (1.32)
. (1.32)
Поскольку
 , (1.33)
, (1.33)
и
 (1.34)
(1.34)
 (1.35)
(1.35)
то
 . (1.36)
. (1.36)
Утверждение теоремы доказано во всех случаях.
Если ввести ранее формулу площади параллелограмма, формулу площади треугольника можно вывести следующим образом.
Пусть в треугольнике АВС сторона ВС равна а, а высота, опущенная на нее, равна h. Достроим треугольник АВС до параллелограмма ABCD, как представлено на рис. 1.14.

Рис.1.14. К выводу формулы площади треугольника
Площадь параллелограмма равна:
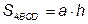 (1.37)
(1.37)
Площадь треугольника АВС равна половине площади параллелограмма, т.к.  . Следовательно,
. Следовательно,

(1.38)
Теорема3. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Доказательство.
Пусть в треугольнике ABC  S – площадь данного треугольника. Докажем, что
S – площадь данного треугольника. Докажем, что

 (1.39)
(1.39)
Введем систему координат с началом в точке С так, чтобы точка В лежала на положительной полуоси Cx, а точка А имела положительную ординату (рис.1.15). Площадь данного треугольника можно вычислить по формуле
 , (1.40)
, (1.40)
где h – высота треугольника. Но h равна ординате точки A, т.е.
 . (1.41)
. (1.41)
Поэтому
 . (1.42)
. (1.42)
Теорема 5. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к ней.
Доказательство.
Пусть дан параллелограмм
ABCD, который изображен на рис. 1.16.
Рис.1.16. К доказательству теоремы 5
Построим прямоугольник FECD со стороной CD и высотой DF. Параллелограмм ABCD составлен из трапеции FBCD и треугольника AFD. Прямоугольник FECD такжесоставлен из трапеции FBCD и треугольника ВЕС, равного треугольнику AFD (по гипотенузе и катету). Отсюда следует, что площадь параллелограмма ABCD равна площади прямоугольника FECD, т.е. равна произведению стороны на высоту, проведенную к ней.
Таким образом, площадь параллелограмма со стороной а и высотой h равна
 (1.43)
(1.43)
Следствие. Площадь параллелограмма равна произведению двух его сторон на синус угла между ними.
Доказательство.
Рассмотрим параллелограмм ABCD (рисунок 22). Высота DF данного параллелограмма равна
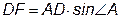 . (1.44)
. (1.44)
Пусть
 . (1.45)
. (1.45)
Тогда площадь S параллелограмма ABCD выражается формулой
 . (1.46)
. (1.46)
Теорема 6. Площадь трапеции равна произведению полусуммы оснований и высоты.
 , (1.47)
, (1.47)
где AD, BC – основания трапеции, H - высота, S – площадь трапеции.
Доказательство.
Рассмотрим трапецию ABCD с основаниями  и высотой ВН. Проведем диагональ BD. Диагональ BD разделяет трапецию на два треугольника ABD и BCD.
и высотой ВН. Проведем диагональ BD. Диагональ BD разделяет трапецию на два треугольника ABD и BCD.
 . (1.48)
. (1.48)
 Примем отрезки AD и ВН за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда
Примем отрезки AD и ВН за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда
(1.49)
Так как
ВН= DH1, (1.50)
то
 . (1.51)
. (1.51)
Тогда
 . (1.52)
. (1.52)
Теорема доказана.
Следствие. Если MN – средняя линия трапеции (рис. 1.17), то

 (1.53)
(1.53)
Рис.1.17 Чертеж к следствию из теоремы 6
Поэтому
 (1.54)
(1.54)
т.е. площадь трапеции равна произведению средней линии на высоту.
Площадь круга
Кругом (рис.1.18) называется фигура, которая состоит из всех точек плоскости, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром круга, а данное расстояние радиусом круга.
Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла.
Круговым сегментом называется общая часть круга и полуплоскости, граница которой содержит хорду этого круга.
Площадь круга равна половине произведения длины ограничивающей его окружности на радиусе:

(1.55)
 Площадь кругового сектора вычисляется по формуле:
Площадь кругового сектора вычисляется по формуле:
(1.56)
 где R – радиус круга,
где R – радиус круга,  - градусная мера соответствующего центрального угла. Если центральный угол
- градусная мера соответствующего центрального угла. Если центральный угол  задан в радианах, то:
задан в радианах, то:
(1.57)

Рис.1.18 Круг
2 Обзор учебно-методического комплекта по геометрии 7-9 классов



 (1.9)
(1.9)

 (рис. 1.9.)
(рис. 1.9.) , площади которых равны
, площади которых равны  . Таким образом, площадь прямоугольника равна
. Таким образом, площадь прямоугольника равна . (1.10)
. (1.10) (1.11)
(1.11)
 и
и 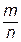 ; второй – со сторонами a и b; третий – со сторонами
; второй – со сторонами a и b; третий – со сторонами  и
и  . Их можно расположить так, что первый прямоугольник не выходит за пределы второго, а третий содержит второй. Это изображено на рис. 1.10.
. Их можно расположить так, что первый прямоугольник не выходит за пределы второго, а третий содержит второй. Это изображено на рис. 1.10. , а площадь третьего составляет
, а площадь третьего составляет  .
. (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14) . (1.15)
. (1.15)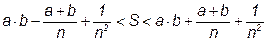 (1.16)
(1.16) . (1.17)
. (1.17) , получаем
, получаем , (1.18)
, (1.18) (1.19)
(1.19) , то это число будет положительным. Выбирая теперь n достаточно большим, можно сделать правую часть неравенства меньше любого положительного числа, а значит, меньше левой его части, если
, то это число будет положительным. Выбирая теперь n достаточно большим, можно сделать правую часть неравенства меньше любого положительного числа, а значит, меньше левой его части, если 

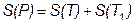
 . (1.21)
. (1.21) (1.22)
(1.22) , (1.23)
, (1.23) (1.24)
(1.24)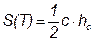 (1.25)
(1.25)

 . (1.28)
. (1.28) , (1.29)
, (1.29) , (1.30)
, (1.30) разбивается отрезком СВ на треугольник Т и прямоугольный треугольник
разбивается отрезком СВ на треугольник Т и прямоугольный треугольник  . Поэтому
. Поэтому . (1.31)
. (1.31) . (1.32)
. (1.32) , (1.33)
, (1.33) (1.35)
(1.35) . (1.36)
. (1.36)
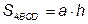 (1.37)
(1.37) . Следовательно,
. Следовательно,
 S – площадь данного треугольника. Докажем, что
S – площадь данного треугольника. Докажем, что
 , (1.40)
, (1.40) . (1.41)
. (1.41)

 (1.43)
(1.43)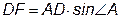 . (1.44)
. (1.44) . (1.45)
. (1.45) . (1.46)
. (1.46) , (1.47)
, (1.47) и высотой ВН. Проведем диагональ BD. Диагональ BD разделяет трапецию на два треугольника ABD и BCD.
и высотой ВН. Проведем диагональ BD. Диагональ BD разделяет трапецию на два треугольника ABD и BCD. . (1.48)
. (1.48) Примем отрезки AD и ВН за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда
Примем отрезки AD и ВН за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда . (1.51)
. (1.51) . (1.52)
. (1.52)
 (1.53)
(1.53) (1.54)
(1.54)
 Площадь кругового сектора вычисляется по формуле:
Площадь кругового сектора вычисляется по формуле: где R – радиус круга,
где R – радиус круга,  - градусная мера соответствующего центрального угла. Если центральный угол
- градусная мера соответствующего центрального угла. Если центральный угол  задан в радианах, то:
задан в радианах, то:


