Дисконтирование. Математическое дисконтирование

Дисконтирование — это определение стоимости денежного потока путём приведения стоимости всех выплат к определённому моменту времени. Дисконтирование является базой для расчётов стоимости денег с учётом фактора времени.

В широком смысле дисконтирование определяется как средство нахождения любой стоимостной величины относящаяся к будущему на более ранний момент времени. Такой прием часто называют приведением стоимостного показателя к некоторому моменту времени.

Принимают два вида дисконтирования:

– математическое (ставка наращения);

– банковское (учетная ставка).

 

При математическом дисконтировании решается задача, обратная определению наращенной суммы. Сформулируем ее следующим образом: какую сумму следует выдать в долг на n лет, чтобы при начислении на нее процентов по ставке i получить наращенную сумму, равную S?

Для решения этой задачи используем формулу наращения по простой ставке процентов (1.4), тогда:

S= P+I= Р + P*n*i = P(1+n*i), (1.4)

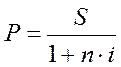(1.42)

где — дисконтный множитель, показывающий, во сколько раз первоначальная сумма ссуды меньше наращенной.

Пример 1.18.

Через один год владелец векселя, выданного коммерческим банком, должен получить по нему 220 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если доходность векселя должна составить 10% годовых?

Решение:

Находим современную (текущую)стоимость:

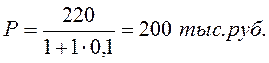
Пример 1.19.

Владелец векселя, номинальная стоимость которого 220 тыс. руб. и сроком обращения 1 год, предъявил его банку для учета за 90 дней до даты погашения. Банк учел его по ставке 12% годовых.

Определить дисконтированную величину (полученную владельцем векселя величину и величину дисконта).

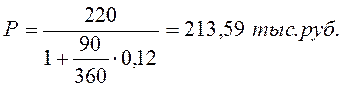— это сумма, полученная владельцем векселя в результате его учета.

Разность S-P=D’ является дисконтом.

В нашем случае дисконт равен:

D’=220-213,59=6,41 тыс.руб.

Действительно, если бы владелец векселя, получивший после его учета 213,59 тыс. руб., вновь поместил его в банк на 90 дней под 12,0% годовых, то по истечении указанного срока он бы получил 220 тыс. руб.

На практике в подобном случае банк обязательно установит для учета ставку более высокую, чем приведена в примере (12,0%), с целью получения большего дисконта, например 13,0%.

БАНКОВСКОЕ ДИСКОНТИРОВАНИЕ (БАНКОВСКИЙ УЧЕТ)

Банковское дисконтирование основано на использовании учетной ставки — d, т.е. проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды.

Пример 1.20.

Вексель номинальной стоимостью 500 тыс. руб. был учтен в банке за 90 дней до срока погашения по учетной ставке 16%.

Определить дисконтированную величину векселя, используя антисипативный (предварительный) метод начисления процентов.

Решение:

Номинальная стоимость векселя — 500 тыс. руб.

Проценты, начисленные на сумму погашения:

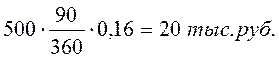
Дисконтированная величина 500 - 20 = 480 тыс. руб.

При банковском дисконтировании дисконтированная величина определяется по формуле:

Р' = S×(1-n·d), (1.44)

где Р' —дисконтированная величина;

S— наращенная сумма долга;

d— учетная (дисконтная) ставка, выраженная в десятичных дробях;

n — временной интервал от момента учета финансового инструмента до даты уплаты по нему в годах.

По данным предыдущего примера и формуле (1.44) рассчитаем дисконтированную величину:

Величина дисконта равна:

D'=S—Р'=500-480=20тыс.руб.

Дисконтирование с помощью математического и банковского методов, т.е. по процентной ставке i и учетной ставке d, приводит к различным финансовым результатам. Например, если в рассматриваемом примере произвести математическое дисконтирование (i = d = 0.16), то дисконтированная величина будет равна

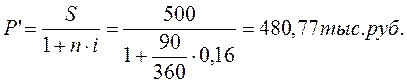
D'=500-480,77=19,23тыс.руб.

 

Как видно, при использовании учетной ставки фактор времени учитывается более строго.

В отдельных случаях может возникнуть ситуация, когда совмещаются начисление процентов по ставке i и дисконтирование по ставке d. При этом наращенная величина ссуды будет определяться по формуле:

S=P×(1+n·i)×(1-n'·d), (1.45)

где Р— сумма, предоставленная в кредит;

n — общий срок платежного обязательства;

n' — срок от момента учета обязательства до даты погашения долга, т.е. n' <n;

S— сумма, полученная при учете обязательства.

Пример 1.21.

Долговое обязательство в сумме 200 тыс. руб. должно быть погашено через 90 дней с процентами (10,5% годовых). Владелец обязательства учел его в банке за 15 дней до наступления срока по учетной ставке 12,5%.

Полученная после учета сумма составила:

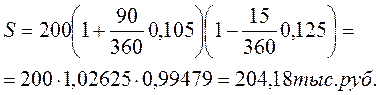
Величина дисконта, полученная банком:

D'=200·1,02625-204,18=205,25-204,18=1,07тыс.руб.

Наряду с приведенными методами дисконтирования существует и ряд других. Так, например, если известна номинальная стоимость долгового обязательства, дисконт можно вычислить по формуле:

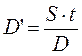(1.46)

Где S— номинальная стоимость долгового обязательства;

t — число дней от момента дисконтирования до даты погашения долга;

D — процентный ключ (дивизор), D = 36 000/i.

Пример 1.22.

Вексель номинальной стоимостью 50 ООО руб. учтен за 15 дней до срока погашения по учетной ставке 12.5% годовых. Определить дисконт и дисконтированную величину.

По формуле (1.46) дисконт будет равен:

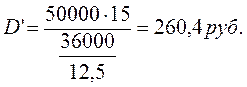
Дисконтированная величина векселя равна

P'=50000-260,4=49739,6 руб.

Для проверки используем ранее приведенную формулу:

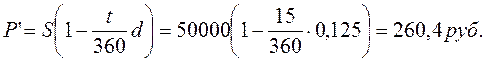
Декурсивная процентная ставка (i), называемая ссудным процентом, – это выраженное в процентах отношение суммы начисленного за определенный интервал дохода I (процентных денег) к сумме, имеющейся на начало данного интервала
- P. Наращение (рост) первоначальной суммы долга – увеличение суммы долга за счет присоединения начисленных процентов.

 

S=P+I (3.1)

I=S-P (3.2)

где S – наращенная сумма.

Коэффициент наращения Кн определяется следующим образом

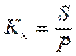, (3.3)

Процентная ставка i является относительной величиной, измеряется в долях единицы и определяется делением процентных денег на первоначальную сумму.

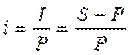, (3.4)

Формула расчета процентной ставки идентична расчету статистического показателя “темп прироста”.

Определение наращенной суммы S называется компаундингом. Определение первоначальной суммы Р – дисконтированием.

День получения и день окончательного погашения займа считаются одним днем (граничный день).

При антисипативном методе начисления (предварительном) процентов проценты выплачиваются в начале периода, за который начисляются проценты. Пример: проценты, взимаемые банком при учете векселей; факторинговый кредит и проч. Величиной получаемого кредита является наращенная сумма S. Исходя из нее, и начисляются проценты. Заемщик получает сумму кредита за вычетом процентов.

Разница между размером кредита S и выдаваемой суммой Р называется дисконтом, обозначается через D и представляет собой сумму процентных денег.

D=S-P, (3.5)

Ставка дисконта, выраженная в долях от единицы и определяемая делением суммы дисконта на величину Р, называется учетной ставкой d.

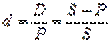, ( 3.6)

Можно заметить, что и сумма процентов I и величина дисконта D определяются одинаковым образом. Однако, в первом случае речь идет о приросте текущей стоимости, своего рода “наценке”, т.е. определяется будущая стоимость “сегодняшних денег”. Во втором случае определяется настоящая стоимость будущих денег, т.е. определяется “скидка” с будущей стоимости (Diskont в переводе с немецкого означает “скидка”).

Чаще всего антисипативный метод используется в чисто технических целях - при дисконтировании, а также при учете векселей в банке, при оплате факторинговых услуг.

Во всех остальных случаях в мировой практике более распространен декурсивный способ начисления процентов. Антисипативный способ применяется в странах с развитой рыночной экономикой в периоды высокой инфляции, так как наращение по антисипативному способу происходит более быстрыми темпами, чем при декурсивном способе начисления.

В хозяйственной практике РБ в настоящее время применяется в основном декурсивный способ начисления простых процентов. Проценты по счетам начисляются в соответствии с договором между банком и клиентом. По счетам учета кредитных и депозитных операций проценты начисляются за период, включающий день выдачи кредита или зачисления денег в депозит, и день предшествующий погашению кредита или выдачи депозита (закрытия счета). При изменении процентной ставки начисление процентов по новой ставке осуществляется со дня ее установления. Количество дней в году (месяце), применяемое при начислении процентов, определяется учетной политикой банка.