

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Тема: Простые проценты
Сущность процентных платежей
Слово «процент» как экономическое понятие в значении "прибыль", "выгода", "преимущество" стало использоваться во второй половине 19 века.
Финансовое определение процента – плата, которую одно лицо (заемщик) передает другому лицу (кредитору) за то, что последний предоставляет первому во временное пользование денежные средства. В современной финансовой лексике процент определяется как плата за использование заемных средств, как цена рентных доходов.
В бизнес-лексике – работать за проценты означает работать за вознаграждение, исчисляемое в зависимости от прибыли или оборота.
Процент и его основные формы:

|
КОМУ
Ссудный процент º процентная ставка.
Процентная ставка характеризует доходность кредитной сделки для кредитора и стоимость кредита для заёмщика. Она показывает, какая доля от суммы выданного кредита будет возвращена владельцу капитала в виде дохода. Поэтому процентная ставка рассчитывается как отношение дохода, полученного за определенный период (чаще всего за год), к величине капитала, предоставляемого в кредит. Величина процентной ставки определяется отношением:
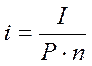 (1.1)
(1.1)
где i – процентная ставка, выраженная в долях единицы (десятичной дробью);
I – величина дохода владельца капитала;
Р – сумма капитала, предоставляемого в кредит;
n – срок ссуды в годах.
Пример 1.1.
Фирма приобрела в банке вексель, по которому через год должна получить 66,0 тыс.руб. (номинальная стоимость векселя). В момент приобретения цена векселя составила 60 тыс.руб.
Определить доходность этой сделки, т.е. размер процентной ставки. [Номинальная стоимость векселя =
Цена продажи векселя * (1 + (срок векселя * ставка / 365*100)) ]
Решение:
По условию задачи первоначальная сумма капитала, предоставляемого в кредит, P=60,0 тыс.руб., номинальная сумма векселя S=66 тыс.руб., доход векселя
I=66-60=6 тыс.руб.
Отсюда 
Таким образом, на каждые вложенные в вексель 1000 руб. фирма получит доход в размере 100,0 руб.
Пример 1.2.
Коммерческий банк приобрёл на 2,0 млн.руб. государственных облигаций со сроком погашения через 6 месяцев. По истечении указанного срока банк рассчитывает получить по облигациям 2140 тыс.руб. Определить доходность ГКО.
Решение:
I=2140-2000=140 тыс.руб.
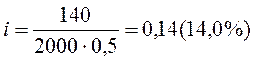
Используя выражение для расчёта процентной ставки, мы можем записать, что величина дохода определяется по формулам:
 (1.2) (Здесь процентная ставка выражена в процентах)
(1.2) (Здесь процентная ставка выражена в процентах)
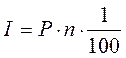 (1.3)
(1.3)
Величину I часто называют процентным доходом, а иногда просто процентами.
В практике используются различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться; в зависимости от этого различают следующие методы начисления процентов:
· по простым процентным ставкам;
· по сложным процентным ставкам;
Сущность метода начисления по простым процентным ставкам сводится к тому, что проценты начисляются в течение всего срока кредита на одну и ту же величину капитала, предоставляемого в кредит.
Метод начисления по сложным процентным ставкам заключается в том, что в первом периоде начисление производится на первоначальную сумму кредита, затем она суммируется с начисленными процентами и в каждом последующем периоде проценты начисляются на уже наращённую сумму. Таким образом, база для начисления процентов постоянно меняется. Иногда этот метод называют «процент на процент».
Другое различие методов начисления процентов заключается в установлении процентной ставки в качестве фиксированной или переменной величины. Так, например, в контракте может быть определена процентная ставка на первый год в одном размере, а на последующие годы предусматривается ее рост (снижение) на определенную величину.
Кроме того, могут применяться «плавающие» ставки, величина которых «привязывается» к темпам инфляции или ставкам рефинансирования, объявляемым Центральным банком, или же ее изменение оговаривается какими-либо другими условиями. Например, в контракте оговаривается первоначальная процентная ставка (базовая ставка), которой пользуются только один период для начисления процентов (допустим, первый квартал), в дальнейшем она будет расти в соответствии с ростом темпов инфляции.
1.2. Вычисление наращённых сумм на основе простых процентных ставок
По условиям кредитного контракта начисленные проценты могут выплачиваться кредитору или по мере их начисления в каждом периоде, или совместно с основной суммой долга по истечении срока контракта. В последнем случае сумма, получаемая кредитором, называется наращённой суммой.
Таким образом, наращенная сумма есть результат сложения суммы, предоставляемой в кредит, и начисленных процентов.
Формула определения наращенной суммы с использованием простых процентов (формула простых процентов) может быть записана в следующем виде:
S= P+I= Р + P*n*i = P(1+n*i), (1.4)
где S — наращённая сумма;
значения символов Р, п, i даны при записи формул (1.1)—(1.3).
Выражение (1+n*i) называется множителем наращения простых процентов.
Пример 1.3.
Банк выдал районной администрации ссуду в размере 4,0 млн руб. сроком на 2 года по ставке простых процентов, равной 11% годовых.
Определить проценты и сумму накопленного долга (наращённую сумму).
Решение:
По условию: Р= 4,0 млн; i= 0,11; n = 2 года;
I=4,0*2*0,11 =0,88 млн руб.;
S= 4,0 + 0,88 = 4,88 млн руб.
или по формуле (1.4)
S=4*(1+2*0,11)= 4,88 млн руб.
Пример 1.4.
Банк выдал кредит 18 января в размере 500,0 тыс. руб. Срок возврата кредита — 3 марта; процентная ставка — 12,0% годовых; год невисокосный. Определить сумму долга, подлежащую возврату. Необходимо рассчитаем се тремя методами.
Точное число дней ссуды определим по табл. 1 (Приложение 1): 62–18=44 дня.
Такой же результат мы получим, рассчитывая число дней по календарю;
С 18.01 по 31.01 включительно— 14дней;
февраль — 28 дней;
март — 3 дня;
итого — 45 дней;
t=45-1=44 дня.
Приближенное число дней ссуды (продолжительность каждого месяца принимается за 30 дней):
январь — 13 дней;
февраль— 30 дней;
март — 3 дня;
всего — 46 дней;
t=46-1=45 дней.
Возможные варианты расчета наращенной суммы:
1) по точным процентам с точным числом дней ссуды:
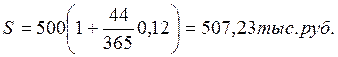
2) по обыкновенным процентам с точным числом дней ссуды:
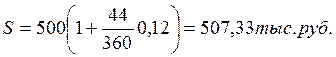
3) по обыкновенным процентам с приближенным числом дней ссуды:
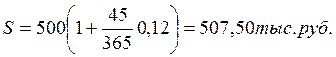
Приведенный пример свидетельствует, что для кредиторов наиболее предпочтительным является третий вариант начисления процентов.
Между величинами процентного дохода, рассчитанными с использованием различной временной базы (I360 и I365) при равном числе дней ссуды (t) существуют следующие соотношения:
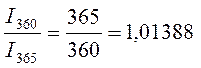 И
И  . (1.6)
. (1.6)
Данные соотношения характеризуют зависимость величины процентного дохода от выбранной временной базы.
По данным примера 1.4(2).
I360=507,33-500=7,33тыс.руб I365=507,23-500=7,23тыс.руб
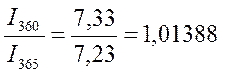 | 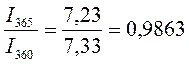 | ||
Эти соотношения также могут быть использованы при определении эквивалентных процентных ставок, т.е. ставок, приносящих одинаковые процентные доходы при различных временных базах, но равных первоначальных капиталах:;
i360=0,9863*i365; i365=1,01388*i360 (1.7)
Пример 1.5.
При выдаче ссуды 500,0 тыс. руб. на 15 дней по ставке 12% годовых, при К=360 дней, наращённая сумма и процентный доход соответственно составят:

I=2,5 тыс.руб
Определить величину процентной ставки, обеспечивающей такой же процентный доход при временной базе К = 365 дней:
Решение:
i365=1,01388*0,12=0,1216656
Проверим это вычисление:
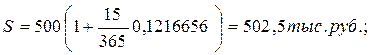
Как указывалось ранее, при заключении кредитного соглашения может быть установлена постоянная на весь период процентная ставка или изменяющаяся (переменная) процентная ставка. При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная сумма определяется по формуле
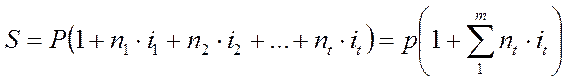 (1.8)
(1.8)
Где it — ставка простых процентов в периоде t;
nt — продолжительность начисления ставки it;
m — число периодов начисления процентов.
Пример 1.6.
Банк предлагает вкладчикам следующие условия по срочному годовому депозиту: в первое полугодие процентная ставка 12,0% годовых, каждый следующий квартал ставка возрастает на 0,5%, Проценты начисляются только на первоначально внесенную сумму вклада.
Определить наращённую за год сумму, если вкладчик поместил в банк на этих условиях 400,0 тыс. руб.:
Решение:

Пример 1.8.
Клиент обратился в банк за кредитом в сумме 800,0 тыс. руб. на срок 270 дней. Банк согласен предоставить кредит на следующих условиях: заёмщик выдаст вексель, обеспечивающий банку доходность от этой операции в размере 12% годовых. Расчет производится с использованием учетной ставки.
Надо определить сумму долга, которая должна будет проставлена в векселе.
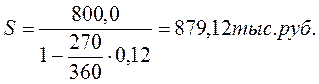
Если бы по приведенным данным начисление процентов производилось по простой процентной ставке, то наращенная сумма оказалась бы значительно меньше:
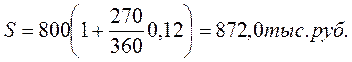
Таким образом, мы убедились, что простая учетная ставка дает более быстрый рост наращенной суммы, чем аналогичная по величине ставка простых процентов.
При равенстве простой процентной ставки (i) и простой учетной ставки (d) различие в величине множителей наращения определяется сроком ссуды, что показано в табл. 1.1.
Таблица 1.1
Пример 1.18.
Через один год владелец векселя, выданного коммерческим банком, должен получить по нему 220 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если доходность векселя должна составить 10% годовых?
Решение:
Находим современную (текущую)стоимость:
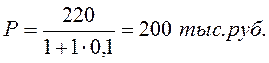
Пример 1.19.
Владелец векселя, номинальная стоимость которого 220 тыс. руб. и сроком обращения 1 год, предъявил его банку для учета за 90 дней до даты погашения. Банк учел его по ставке 12% годовых.
Определить дисконтированную величину (полученную владельцем векселя величину и величину дисконта).
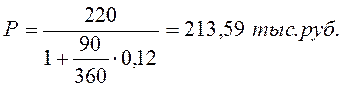 — это сумма, полученная владельцем векселя в результате его учета.
— это сумма, полученная владельцем векселя в результате его учета.
Разность S-P=D’ является дисконтом.
В нашем случае дисконт равен:
D’=220-213,59=6,41 тыс.руб.
Действительно, если бы владелец векселя, получивший после его учета 213,59 тыс. руб., вновь поместил его в банк на 90 дней под 12,0% годовых, то по истечении указанного срока он бы получил 220 тыс. руб.
На практике в подобном случае банк обязательно установит для учета ставку более высокую, чем приведена в примере (12,0%), с целью получения большего дисконта, например 13,0%.
Пример 1.20.
Вексель номинальной стоимостью 500 тыс. руб. был учтен в банке за 90 дней до срока погашения по учетной ставке 16%.
Определить дисконтированную величину векселя, используя антисипативный (предварительный) метод начисления процентов.
Решение:
Номинальная стоимость векселя — 500 тыс. руб.
Проценты, начисленные на сумму погашения:
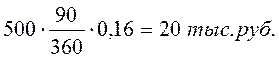
Дисконтированная величина 500 - 20 = 480 тыс. руб.
При банковском дисконтировании дисконтированная величина определяется по формуле:
Р' = S×(1-n·d), (1.44)
где Р' —дисконтированная величина;
S— наращенная сумма долга;
d— учетная (дисконтная) ставка, выраженная в десятичных дробях;
n — временной интервал от момента учета финансового инструмента до даты уплаты по нему в годах.
По данным предыдущего примера и формуле (1.44) рассчитаем дисконтированную величину:

Величина дисконта равна:
D'=S—Р'=500-480=20тыс.руб.
Дисконтирование с помощью математического и банковского методов, т.е. по процентной ставке i и учетной ставке d, приводит к различным финансовым результатам. Например, если в рассматриваемом примере произвести математическое дисконтирование (i = d = 0.16), то дисконтированная величина будет равна
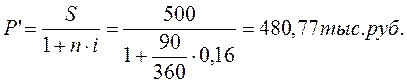
D'=500-480,77=19,23тыс.руб.
Как видно, при использовании учетной ставки фактор времени учитывается более строго.
В отдельных случаях может возникнуть ситуация, когда совмещаются начисление процентов по ставке i и дисконтирование по ставке d. При этом наращенная величина ссуды будет определяться по формуле:
S=P×(1+n·i)×(1-n'·d), (1.45)
где Р— сумма, предоставленная в кредит;
n — общий срок платежного обязательства;
n' — срок от момента учета обязательства до даты погашения долга, т.е. n' <n;
S— сумма, полученная при учете обязательства.
Пример 1.21.
Долговое обязательство в сумме 200 тыс. руб. должно быть погашено через 90 дней с процентами (10,5% годовых). Владелец обязательства учел его в банке за 15 дней до наступления срока по учетной ставке 12,5%.
Полученная после учета сумма составила:
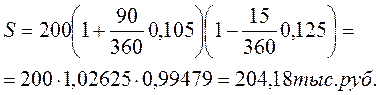
Величина дисконта, полученная банком:
D'=200·1,02625-204,18=205,25-204,18=1,07тыс.руб.
Наряду с приведенными методами дисконтирования существует и ряд других. Так, например, если известна номинальная стоимость долгового обязательства, дисконт можно вычислить по формуле:
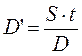 (1.46)
(1.46)
Где S— номинальная стоимость долгового обязательства;
t — число дней от момента дисконтирования до даты погашения долга;
D — процентный ключ (дивизор), D = 36 000/i.
Пример 1.22.
Вексель номинальной стоимостью 50 ООО руб. учтен за 15 дней до срока погашения по учетной ставке 12.5% годовых. Определить дисконт и дисконтированную величину.
По формуле (1.46) дисконт будет равен:
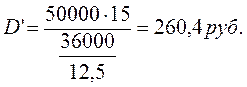
Дисконтированная величина векселя равна
P'=50000-260,4=49739,6 руб.
Для проверки используем ранее приведенную формулу:
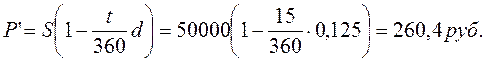
Декурсивная процентная ставка (i), называемая ссудным процентом, – это выраженное в процентах отношение суммы начисленного за определенный интервал дохода I (процентных денег) к сумме, имеющейся на начало данного интервала
- P. Наращение (рост) первоначальной суммы долга – увеличение суммы долга за счет присоединения начисленных процентов.
S=P+I (3.1)
I=S-P (3.2)
где S – наращенная сумма.
Коэффициент наращения Кн определяется следующим образом
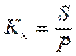 , (3.3)
, (3.3)
Процентная ставка i является относительной величиной, измеряется в долях единицы и определяется делением процентных денег на первоначальную сумму.
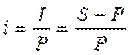 , (3.4)
, (3.4)
Формула расчета процентной ставки идентична расчету статистического показателя “темп прироста”.
Определение наращенной суммы S называется компаундингом. Определение первоначальной суммы Р – дисконтированием.
День получения и день окончательного погашения займа считаются одним днем (граничный день).
При антисипативном методе начисления (предварительном) процентов проценты выплачиваются в начале периода, за который начисляются проценты. Пример: проценты, взимаемые банком при учете векселей; факторинговый кредит и проч. Величиной получаемого кредита является наращенная сумма S. Исходя из нее, и начисляются проценты. Заемщик получает сумму кредита за вычетом процентов.
Разница между размером кредита S и выдаваемой суммой Р называется дисконтом, обозначается через D и представляет собой сумму процентных денег.
D=S-P, (3.5)
Ставка дисконта, выраженная в долях от единицы и определяемая делением суммы дисконта на величину Р, называется учетной ставкой d.
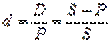 , ( 3.6)
, ( 3.6)
Можно заметить, что и сумма процентов I и величина дисконта D определяются одинаковым образом. Однако, в первом случае речь идет о приросте текущей стоимости, своего рода “наценке”, т.е. определяется будущая стоимость “сегодняшних денег”. Во втором случае определяется настоящая стоимость будущих денег, т.е. определяется “скидка” с будущей стоимости (Diskont в переводе с немецкого означает “скидка”).
Чаще всего антисипативный метод используется в чисто технических целях - при дисконтировании, а также при учете векселей в банке, при оплате факторинговых услуг.
Во всех остальных случаях в мировой практике более распространен декурсивный способ начисления процентов. Антисипативный способ применяется в странах с развитой рыночной экономикой в периоды высокой инфляции, так как наращение по антисипативному способу происходит более быстрыми темпами, чем при декурсивном способе начисления.
В хозяйственной практике РБ в настоящее время применяется в основном декурсивный способ начисления простых процентов. Проценты по счетам начисляются в соответствии с договором между банком и клиентом. По счетам учета кредитных и депозитных операций проценты начисляются за период, включающий день выдачи кредита или зачисления денег в депозит, и день предшествующий погашению кредита или выдачи депозита (закрытия счета). При изменении процентной ставки начисление процентов по новой ставке осуществляется со дня ее установления. Количество дней в году (месяце), применяемое при начислении процентов, определяется учетной политикой банка.
Тема: Простые проценты
Сущность процентных платежей
Слово «процент» как экономическое понятие в значении "прибыль", "выгода", "преимущество" стало использоваться во второй половине 19 века.
Финансовое определение процента – плата, которую одно лицо (заемщик) передает другому лицу (кредитору) за то, что последний предоставляет первому во временное пользование денежные средства. В современной финансовой лексике процент определяется как плата за использование заемных средств, как цена рентных доходов.
В бизнес-лексике – работать за проценты означает работать за вознаграждение, исчисляемое в зависимости от прибыли или оборота.
Процент и его основные формы:

|
КОМУ
Ссудный процент º процентная ставка.
Процентная ставка характеризует доходность кредитной сделки для кредитора и стоимость кредита для заёмщика. Она показывает, какая доля от суммы выданного кредита будет возвращена владельцу капитала в виде дохода. Поэтому процентная ставка рассчитывается как отношение дохода, полученного за определенный период (чаще всего за год), к величине капитала, предоставляемого в кредит. Величина процентной ставки определяется отношением:
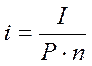 (1.1)
(1.1)
где i – процентная ставка, выраженная в долях единицы (десятичной дробью);
I – величина дохода владельца капитала;
Р – сумма капитала, предоставляемого в кредит;
n – срок ссуды в годах.
Пример 1.1.
Фирма приобрела в банке вексель, по которому через год должна получить 66,0 тыс.руб. (номинальная стоимость векселя). В момент приобретения цена векселя составила 60 тыс.руб.
Определить доходность этой сделки, т.е. размер процентной ставки. [Номинальная стоимость векселя =
Цена продажи векселя * (1 + (срок векселя * ставка / 365*100)) ]
Решение:
По условию задачи первоначальная сумма капитала, предоставляемого в кредит, P=60,0 тыс.руб., номинальная сумма векселя S=66 тыс.руб., доход векселя
I=66-60=6 тыс.руб.
Отсюда 
Таким образом, на каждые вложенные в вексель 1000 руб. фирма получит доход в размере 100,0 руб.
Пример 1.2.
Коммерческий банк приобрёл на 2,0 млн.руб. государственных облигаций со сроком погашения через 6 месяцев. По истечении указанного срока банк рассчитывает получить по облигациям 2140 тыс.руб. Определить доходность ГКО.
Решение:
I=2140-2000=140 тыс.руб.
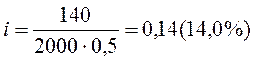
Используя выражение для расчёта процентной ставки, мы можем записать, что величина дохода определяется по формулам:
 (1.2) (Здесь процентная ставка выражена в процентах)
(1.2) (Здесь процентная ставка выражена в процентах)
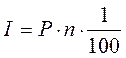 (1.3)
(1.3)
Величину I часто называют процентным доходом, а иногда просто процентами.
В практике используются различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться; в зависимости от этого различают следующие методы начисления процентов:
· по простым процентным ставкам;
· по сложным процентным ставкам;
Сущность метода начисления по простым процентным ставкам сводится к тому, что проценты начисляются в течение всего срока кредита на одну и ту же величину капитала, предоставляемого в кредит.
Метод начисления по сложным процентным ставкам заключается в том, что в первом периоде начисление производится на первоначальную сумму кредита, затем она суммируется с начисленными процентами и в каждом последующем периоде проценты начисляются на уже наращённую сумму. Таким образом, база для начисления процентов постоянно меняется. Иногда этот метод называют «процент на процент».
Другое различие методов начисления процентов заключается в установлении процентной ставки в качестве фиксированной или переменной величины. Так, например, в контракте может быть определена процентная ставка на первый год в одном размере, а на последующие годы предусматривается ее рост (снижение) на определенную величину.
Кроме того, могут применяться «плавающие» ставки, величина которых «привязывается» к темпам инфляции или ставкам рефинансирования, объявляемым Центральным банком, или же ее изменение оговаривается какими-либо другими условиями. Например, в контракте оговаривается первоначальная процентная ставка (базовая ставка), которой пользуются только один период для начисления процентов (допустим, первый квартал), в дальнейшем она будет расти в соответствии с ростом темпов инфляции.
1.2. Вычисление наращённых сумм на основе простых процентных ставок
По условиям кредитного контракта начисленные проценты могут выплачиваться кредитору или по мере их начисления в каждом периоде, или совместно с основной суммой долга по истечении срока контракта. В последнем случае сумма, получаемая кредитором, называется наращённой суммой.
Таким образом, наращенная сумма есть результат сложения суммы, предоставляемой в кредит, и начисленных процентов.
Формула определения наращенной суммы с использованием простых процентов (формула простых процентов) может быть записана в следующем виде:
S= P+I= Р + P*n*i = P(1+n*i), (1.4)
где S — наращённая сумма;
значения символов Р, п, i даны при записи формул (1.1)—(1.3).
Выражение (1+n*i) называется множителем наращения простых процентов.
Пример 1.3.
Банк выдал районной администрации ссуду в размере 4,0 млн руб. сроком на 2 года по ставке простых процентов, равной 11% годовых.
Определить проценты и сумму накопленного долга (наращённую сумму).
Решение:
По условию: Р= 4,0 млн; i= 0,11; n = 2 года;
I=4,0*2*0,11 =0,88 млн руб.;
S= 4,0 + 0,88 = 4,88 млн руб.
или по формуле (1.4)
S=4*(1+2*0,11)= 4,88 млн руб.
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
© cyberpedia.su 2017-2026 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!