В этом разделе приведены варианты развития механических и гидромеханических процессов: вибросепарирование для обработки зерновых, масличных и крупяных культур; измельчение и жиловка мясного сырья, смешивание и формование помадной массы, фильтрование суспензий.
Выявлены основные факторы, влияющие на эффективность протекания этих процессов и определены перспективные направления совершенствования конструкций, сущность технической новизны которых приведена в разделе 13.1.
Процесс сепарирования зерновых, масличных и крупяных культур, модельные представления которого сформулированы Оспановым А.Б.
 Рис. 10.6. Схема сепарирующего органа (а) и технологического процесса разделения зерносмеси (б)
Рис. 10.6. Схема сепарирующего органа (а) и технологического процесса разделения зерносмеси (б)
|
В основу данного процесса положен принцип послойного разделения зерновых смесей (рис. 10.6, б) в сепарирующем органе (рис. 10.6, а), состоящем из кольцевой опорной поверхности 1 с радиальными рифлями 2, наружного 3 и внутреннего 4 концентричных порогов. Наружный кольцевой порог 3 в нижней части имеет равномерно распределенных по периметру выпускных отверстий 5.
Зерновая смесь (рис. 10.6, б), состоящая из зерен пшеницы и семян сорных растений, непрерывно подается на средний радиус кольцевого канала, совершающего вращательные колебания вокруг неподвижной вертикальной оси, где при совокупном воздействии гравитационных сил и сил тангенциальной и нормальной инерции зерносмесь в кольцевом канале занимает объем, верхняя свободная поверхность которого близка конической с образующей, поднимающейся по мере удаления от оси колебаний. В силу воздействия радиальных рифлей зерносмесь самосортируется, ее плотные и мелкие частицы (зерна основной культуры) погружаются в нижние слои и транспортируются радиальными рифлями к наружному кольцевому порогу 3 и выводятся через выпускные отверстия 5, а семена сорных растений, как менее плотные и крупные, всплывают на поверхность зерносмеси. И под действием подпора зерен основной культуры и сил гравитации скатываются по наклонной свободной поверхности зерносмеси к внутреннему кольцевому порогу 4, и переливаются через его верхнюю кромку.
Рассмотрено условие динамического равновесия элементарной массы dm, расположенной на радиусе R внутри элементарного слоя n в виде материального кольца с бесконечно малой толщиной (рис. 10.7, а).
 Рис. 10.7. Схема послойного движения зерносмеси
Рис. 10.7. Схема послойного движения зерносмеси
|
Опорная поверхность за полпериода колебаний совершает вращательное ускоренное движение с угловым ускорением  , при котором происходит послойное движение сыпучего тела по всей его толщине и ширине кольцевого канала. Поскольку скорость элементарного слоя п (рис. 10.7, б, проекция сечения сыпучего тела в плоскости KZ) больше, чем вышележащего слоя (п - 1), и меньше, чем скорость нижележащего (п + 1), то сила трения
, при котором происходит послойное движение сыпучего тела по всей его толщине и ширине кольцевого канала. Поскольку скорость элементарного слоя п (рис. 10.7, б, проекция сечения сыпучего тела в плоскости KZ) больше, чем вышележащего слоя (п - 1), и меньше, чем скорость нижележащего (п + 1), то сила трения  со стороны вышележащего слоя препятствует его движению, а сила трения
со стороны вышележащего слоя препятствует его движению, а сила трения  со стороны нижележащего слоя способствует его движению. Следовательно, разность этих сил трения должна быть уравновешена силой инерции dРu данного элемента объема в абсолютном движении. При этом пренебрегаем радиальным перемещением элемента объема за полпериода колебаний опорной поверхности.
со стороны нижележащего слоя способствует его движению. Следовательно, разность этих сил трения должна быть уравновешена силой инерции dРu данного элемента объема в абсолютном движении. При этом пренебрегаем радиальным перемещением элемента объема за полпериода колебаний опорной поверхности.
Тогда уравнение равновесия слоя n примет вид
 , (10.5)
, (10.5)
где  - тангенциальная сила инерции элемента объема в абсолютном движении, где
- тангенциальная сила инерции элемента объема в абсолютном движении, где  - абсолютное угловое ускорение слоя п;
- абсолютное угловое ускорение слоя п;  и
и  - силы трения со стороны смежных слоев, где
- силы трения со стороны смежных слоев, где 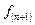 и
и 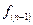 -коэффициенты сопротивления относительному сдвигу нижележащего (п + 1) и вышележащего (n - 1) слоев; G и dG - давления, соответственно вышележащей части зерносмеси и элемента объема, отнесенные на единицу площади опорной поверхности.
-коэффициенты сопротивления относительному сдвигу нижележащего (п + 1) и вышележащего (n - 1) слоев; G и dG - давления, соответственно вышележащей части зерносмеси и элемента объема, отнесенные на единицу площади опорной поверхности.
После преобразования (10.5) имеем
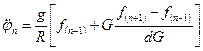 . (10.6)
. (10.6)
Выражение в квадратных скобках следует считать как приведенный коэффициент сопротивления сдвигу слоя  .
.
Считаем, что приведенный коэффициент сопротивления сдвигу слоев  является возрастающей функцией силы тяжести G вышележащей части зерносмеси и зависимость
является возрастающей функцией силы тяжести G вышележащей части зерносмеси и зависимость  близка к линейной.
близка к линейной.
Тогда из эпюры (рис. 10.7, в) имеем  и
и  , где f 0 - коэффициент сопротивления сдвигу слоя, расположенного на верхней свободной границе зерносмеси;
, где f 0 - коэффициент сопротивления сдвигу слоя, расположенного на верхней свободной границе зерносмеси;  и
и  - приращения коэффициентов сопротивления сдвигу соответственно слоев (n + 1) и (n - 1);
- приращения коэффициентов сопротивления сдвигу соответственно слоев (n + 1) и (n - 1);  - разность коэффициентов сопротивления сдвигу нижней и верхней границ зерносмеси; Gm - давление всей подвижной части зерносмеси на единицу площади опорной поверхности.
- разность коэффициентов сопротивления сдвигу нижней и верхней границ зерносмеси; Gm - давление всей подвижной части зерносмеси на единицу площади опорной поверхности.
Уравнение (10.6) после преобразований примет вид
 . (10.7)
. (10.7)
Считая массу элемента объема бесконечно малой, пренебрегаем членом  . Введя безразмерные переменные
. Введя безразмерные переменные 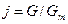 и
и  , позволяющие оценить интенсивность послойного движения зерносмеси через ее механические свойства, получим
, позволяющие оценить интенсивность послойного движения зерносмеси через ее механические свойства, получим
 . (10.8)
. (10.8)
Поскольку fт > f 0, то очевидно, что на радиусе R послойное движение по всей толщине зерносмеси возможно при условии  . В данном случае угловое ускорение опорной поверхности должно удовлетворить неравенству
. В данном случае угловое ускорение опорной поверхности должно удовлетворить неравенству 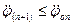 .Если
.Если  , то зерносмесь остается неподвижным относительно опорной поверхности. При постепенном увеличении углового ускорения опорной поверхности на радиусе R свое относительное движение начинают частицы, расположенные на верхней границе (j = 0) зерносмеси, при первом критическом значении углового ускорения
, то зерносмесь остается неподвижным относительно опорной поверхности. При постепенном увеличении углового ускорения опорной поверхности на радиусе R свое относительное движение начинают частицы, расположенные на верхней границе (j = 0) зерносмеси, при первом критическом значении углового ускорения 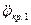 опорной поверхности, а затем движение постепенно распространяется в нижние слои. При достижении второго критического значения
опорной поверхности, а затем движение постепенно распространяется в нижние слои. При достижении второго критического значения  начинают относительное движение частицы, расположенные на нижней границе (j = 1) зерносмеси. В дальнейшем увеличении ускорения опорной поверхности (
начинают относительное движение частицы, расположенные на нижней границе (j = 1) зерносмеси. В дальнейшем увеличении ускорения опорной поверхности (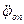 >>
>>  ) зерносмесь будет стремиться к абсолютно неподвижному состоянию, т.е. прекращению послойного движения. Если опорная поверхность совершает гармонические вращательные колебания по закону
) зерносмесь будет стремиться к абсолютно неподвижному состоянию, т.е. прекращению послойного движения. Если опорная поверхность совершает гармонические вращательные колебания по закону  , где j0 и w - соответственно, угловые амплитуда и частота колебаний опорной поверхности, то можно представить критические значения ее угловой скорости
, где j0 и w - соответственно, угловые амплитуда и частота колебаний опорной поверхности, то можно представить критические значения ее угловой скорости
 , (10.9)
, (10.9)
 . (10.10)
. (10.10)
Как видно из (10.10), если известны коэффициенты сопротивления сдвигу верхнего f 0 и нижнего fт слоев и значение угловой амплитуды  , то для любой радиальной координаты R можно определить значение частоты колебаний w кр.2 кольцевого канала, при котором по всей толщине зерновой смеси будет протекать послойное движение, обусловливающее интенсивное самосортирование зерносмеси.
, то для любой радиальной координаты R можно определить значение частоты колебаний w кр.2 кольцевого канала, при котором по всей толщине зерновой смеси будет протекать послойное движение, обусловливающее интенсивное самосортирование зерносмеси.
* * *
Предложенная модель послужила основой формирования технологического процесса самосортирования зерновых материалов в шероховатом кольцевом канале, совершающем вращательные колебания вокруг вертикальной неподвижной оси.
Процесс измельчения мясного сырья, модельные представления которого сформулированы Божьевым С.В.
Построена физическая модель (рис. 10.8.) процессов, происходящих в режущем механизме волчка, в которой учтены затраты энергии на собственно процесс резания, на процесс истечения кускового сырья через отверстия, на явления, сопутствующие перемешиванию мяса вращающейся лопастью ножа и, наконец, на трение в механизме, вызывающем изменение температуры.
Часть усилия, создаваемого подающим механизмом, определяется по формуле:
 . (10.11)
. (10.11)
В общем виде:
 . (10.12)
. (10.12)
 Рис. 10.8. Физическая модель процесса резания:
1 - крестовой нож; 2 - измельчаемое сырье; 3 - ножевая решетка;
F 1 - сила сопротивления перерезанию волокон сырья; F 2 - сила сопротивления перемешиванию; F 3 - силы трения между режущими плоскостями ножа и решетками; F 4 - усилие затяжки режущего механизма; F 5 - силы трения ножа и сырье; a - угол резания; Q - общее усилие резания; Q 1 - часть усилия, создаваемого подающим механизмом; Р 1, Р 2 - сопротивления проталкиванию сырья через отверстия решетки; w - угловая скорость вращения ножа.
Рис. 10.8. Физическая модель процесса резания:
1 - крестовой нож; 2 - измельчаемое сырье; 3 - ножевая решетка;
F 1 - сила сопротивления перерезанию волокон сырья; F 2 - сила сопротивления перемешиванию; F 3 - силы трения между режущими плоскостями ножа и решетками; F 4 - усилие затяжки режущего механизма; F 5 - силы трения ножа и сырье; a - угол резания; Q - общее усилие резания; Q 1 - часть усилия, создаваемого подающим механизмом; Р 1, Р 2 - сопротивления проталкиванию сырья через отверстия решетки; w - угловая скорость вращения ножа.
|
Учтены следующие силы: Q 1 - силы, создаваемые подающим механизмом; Q - силы, создаваемые режущим механизмом; Рi - силы, необходимые на истечение сырья.
Силы, создаваемые режущим механизмом, необходимы для перерезания сырья сдвигом:
 , (10.13)
, (10.13)
где t m - предел текучести продукта при чистом сдвиге (Па); d 0 - диаметр отверстий решетки (м); L - толщина решетки (м).
Полезная мощность N 1, затрачиваемая на срез продукта вращающимся ножом, определяется по формуле:
 , (10.14)
, (10.14)
где М - суммарный момент всех срезывающих сил относительно оси вращения ножа, w- угловая скорость вращения ножа. Величину момента М найдём как арифметическую сумму моментов всех срезывающих сил относительно оси вращения ножа:
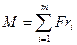 или
или  , (10.15)
, (10.15)
где т - количество отверстий, с которых срезается продукт в каждый данный момент времени; ri - расстояние от центра каждого отверстия, с которого срезается продукт, до оси вращения ножа.
Если угловую скорость w ножа выразить через число оборотов в минуту, то с учётом равенств (10.14) и (10.15), формула (10.13) примет вид:
 . (10.16)
. (10.16)
Расчетная схема для определения сил сухого трения ножа о решетку представлена на рис. 10.9.
 Рис. 10.9. Расчетная схема для определения сил сухого трения ножа о решетку:
АВD - один из четырех перьев серповидного ножа; ABC - равнобедренный треугольник, равный по площади АВD; r - произвольное расстояние от оси вращения до элементарной площадки ножа; l - длина узкой элементарной площадки; dr - ширина площадки; dF - сила трения действующая на элементарную площадку; р - давление ножа на часть решетки; v - скорость центра площадки; h - высота ножа от его основания (сторона квадрата); R - расстояние от вершины условного ножа до оси вращения; R 0 - радиус окружности в которую вписан четырехугольник.
Рис. 10.9. Расчетная схема для определения сил сухого трения ножа о решетку:
АВD - один из четырех перьев серповидного ножа; ABC - равнобедренный треугольник, равный по площади АВD; r - произвольное расстояние от оси вращения до элементарной площадки ножа; l - длина узкой элементарной площадки; dr - ширина площадки; dF - сила трения действующая на элементарную площадку; р - давление ножа на часть решетки; v - скорость центра площадки; h - высота ножа от его основания (сторона квадрата); R - расстояние от вершины условного ножа до оси вращения; R 0 - радиус окружности в которую вписан четырехугольник.
|
Мощность, затрачиваемая на преодоление сил сухого трения, равна:
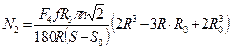 ,(10.17)
,(10.17)
где S 0 - часть площади ножа, занятой отверстиями решётки  ; d 0 - диаметр отверстия; k - количество отверстий, перекрываемых одним ножом; S - площадь одного ножа; f - коэффициент трения скольжения ножа о металлическую часть решётки.
; d 0 - диаметр отверстия; k - количество отверстий, перекрываемых одним ножом; S - площадь одного ножа; f - коэффициент трения скольжения ножа о металлическую часть решётки.
Определяем перепад давления, необходимого для проталкивания мяса через отверстия модифицированной решётки.
На рис. 10.10 показано отверстие модифицированной решётки, представляющей два симметричных круговых конических канала со сходящимся (конфузорным) и расходящимся (диффузорным) участками.
Мощность N 3, необходимая для продвижения продукта по каналу (отверстию решётки), равна 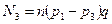 , или
, или
 , (10.18)
, (10.18)
где m е - эквивалентная вязкость (используем модель бингамовской среды); n - общее количество отверстий в решетке; С - постоянная величина.
Процесс резания мяса сопровождается перемешиванием измельчённого мяса в пространстве между решётками.
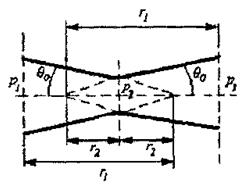 Рис. 10.10. Отверстие модифиванной решетки:
р 1 - давления на входе в канал; r 1 - расстояние вершин конуса, находящиеся на продолжении канала (для входного и выходного участка); р 2 - давление в наиболее узкой части канала; р 3 - давление на выходе из канала; q0 - половина угла раствора каждого из конусов; r 2 - расстояние от вершины каждого конуса до середины канала.
Рис. 10.10. Отверстие модифиванной решетки:
р 1 - давления на входе в канал; r 1 - расстояние вершин конуса, находящиеся на продолжении канала (для входного и выходного участка); р 2 - давление в наиболее узкой части канала; р 3 - давление на выходе из канала; q0 - половина угла раствора каждого из конусов; r 2 - расстояние от вершины каждого конуса до середины канала.
|
На рис. 10.11. показано прямоугольное лобовое сечение одного ножа.
 Рис. 10.11. Наибольшее лобовое сечение одного ножа, вращающегося вокруг вертикальной оси:
w - угловая скорость вращения ножа; h - высота сечения ножа; dr - длина элементарной площадки; r - расстояние от оси вращения ножа до элементарной площадки; R - расстояние от оси вращения ножа до его конечной точки; dF - сила лобового сопротивления, действующая на элементарную площадку; v - скорость движения в элементарной площадки ножа; R 0 - радиус окружности на которую опирается каждое перо ножа
Рис. 10.11. Наибольшее лобовое сечение одного ножа, вращающегося вокруг вертикальной оси:
w - угловая скорость вращения ножа; h - высота сечения ножа; dr - длина элементарной площадки; r - расстояние от оси вращения ножа до элементарной площадки; R - расстояние от оси вращения ножа до его конечной точки; dF - сила лобового сопротивления, действующая на элементарную площадку; v - скорость движения в элементарной площадки ножа; R 0 - радиус окружности на которую опирается каждое перо ножа
|
Мощности сил сопротивления при перемешивании сырья лопастью ножа определяем по формуле:
 , (10.19)
, (10.19)
где s - коэффициент пропорциональности, зависящий от свойств продукта.
Определяем степень нагрева продукта за счёт механической работы.
Суммируя мощности N 1, N 2, N 3, N 4и умножая их сумму на время работы t, найдём часть механической работы, совершаемой непосредственно по резанию мяса
А = (N 1 + N 2 + N 3 +N 4) t. (10.20)
Для оценочных расчётов примем, что работа, затрачиваемая на преодоление всех сил сопротивлений, полностью переходит в тепло, которое, не рассеиваясь, идёт на нагревание продукта. В этом случае величина работы А будет равна количеству выделившегося тепла А = Q = с×т (Т 2 - T 1), где т - масса нагреваемого продукта; с - удельная теплоёмкость продукта; Т 1- начальная температура продукта; Т 2- конечная температура продукта. Подставив данное выражение работы в равенство (10.20) и разделив его левую и правую части на время t,получим:
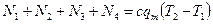 , (10.21)
, (10.21)
где  - массовый расход продукта, откуда находим разность температур
- массовый расход продукта, откуда находим разность температур
 . (10.22)
. (10.22)
Общая мощность процесса резания определяется по формуле:
 . (10.23)
. (10.23)
* * *
Представленная математическая модель позволяет рассчитать энергетические затраты на процесс резания и процесс истечения мяса через отверстия решетки, что дает возможность обосновать применение раздельных приводов для вращения шнека и вала режущего механизма.
 Рис. 10.12. Математическая модель
процесса жиловки
Рис. 10.12. Математическая модель
процесса жиловки
|
Процесс жиловки мясного сырья, модельные представления которого сформулированы Комисаровым С.С.
В качестве приближенной математической модели процесса рассмотрим модель движения материальной точки по перу ножа (рис. 10.12).
Рассмотрим движение частицы в промежутке между промежуточной, выходной решетками и ножом. Движение продукта в этом пространстве является сложным движением. В качестве относительного движения принимаем движение продукта по поверхности решетки, а переносное движение – вращение частицы вместе с пером ножа.
В относительном движении на частицу действуют сила тяжести 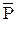 , нормальная реакция со стороны диска
, нормальная реакция со стороны диска  , нормальная реакция со стороны лопасти
, нормальная реакция со стороны лопасти  , соответствующие силы трения
, соответствующие силы трения 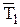 и
и  , а также переносная сила инерции
, а также переносная сила инерции  и кориолисова сила инерции
и кориолисова сила инерции 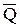 .
.
В этом случае векторное уравнение относительного движения имеет вид
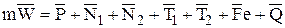 . (10.24)
. (10.24)
Проецируя уравнение (10.24) на декартовы оси координат  , получим дифференциальное уравнение относительного движения системы в проекциях на эти оси
, получим дифференциальное уравнение относительного движения системы в проекциях на эти оси
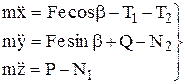 . (10.25)
. (10.25)
Так как движение частицы относительно оси  ограничено поверхностью решетки, то равнодействующая сил равна нулю
ограничено поверхностью решетки, то равнодействующая сил равна нулю
 , (10.26)
, (10.26)
следовательно, из уравнения (10.25)
 (10.27)
(10.27)
где  - масса частицы продукта, кг;
- масса частицы продукта, кг;  - ускорение свободного падения (
- ускорение свободного падения ( м/с2).
м/с2).
Движение продукта относительно оси  также ограничено пером ножа и равнодействующая проекций сил действующих на частицу продукта в относительном движении, на ось
также ограничено пером ножа и равнодействующая проекций сил действующих на частицу продукта в относительном движении, на ось  равна нулю, то есть
равна нулю, то есть
 . (10.28)
. (10.28)
Из уравнения (10.28) найдем величину силы нормального давления пера ножа на частицу
 . (10.29)
. (10.29)
Как известно, переносная сила инерции равна
 (10.30)
(10.30)
где 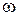 - угловая скорость вращения ротора, рад/с;
- угловая скорость вращения ротора, рад/с; 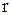 - радиус вращения частиц, м.
- радиус вращения частиц, м.
А кориолисова сила инерции
 , (10.31)
, (10.31)
где  - относительная скорость частицы, м/с.
- относительная скорость частицы, м/с.
Тогда уравнение (10.29) после преобразований примет вид

 (10.32)
(10.32)
Так как угол между векторами относительной скорости частицы  и угловой скорости вращения
и угловой скорости вращения  равен 90°, то уравнение (10.32) перепишется в виде
равен 90°, то уравнение (10.32) перепишется в виде
 . (10.33)
. (10.33)
Согласно гипотезе Амонтона-Кулона сила сухого трения прямопропорциональна величине силы нормального давления и направлена в сторону, противоположную движению
 , (10.34)
, (10.34)
 , (10.35)
, (10.35)
где 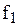 =
= 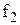 - соответственно коэффициенты трения продукта о поверхность решетки и перо ножа (для материалов мясо-сталь
- соответственно коэффициенты трения продукта о поверхность решетки и перо ножа (для материалов мясо-сталь  ).
).
Тогда дифференциальное уравнение относительного движения частицы запишется следующим образом
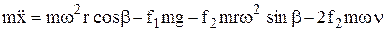 . (10.36)
. (10.36)
Рассмотрим DОАВ, в котором ÐОАВ=b. Тогда по теореме о перекрещивающихся углах имеем
 . (10.37)
. (10.37)
Подставляя систему (10.37) в уравнение (10.36) и сокращая все выражение на  получим
получим
 . (10.38)
. (10.38)
Рассмотрим DОСВ, в котором ÐОСВ=b0 – угол наклона лопасти ротора относительно радиального направления, тогда
 . (10.39)
. (10.39)
Подставляя (10.39) в уравнение (10.38) получим окончательный вид дифференциального уравнения относительного движения частицы продукта в промежутке между промежуточной, выходной решетками и ножом.
 . (10.40)
. (10.40)
Полученное дифференциальное уравнение (10.40) второго порядка является нелинейным и аналитического решения не имеет. Поэтому для его решения воспользуемся численным методом Рунге-Кутта четвертого порядка. Для этого приведем данное дифференциальное уравнение второго порядка к системе нелинейных дифференциальных уравнений первого порядка
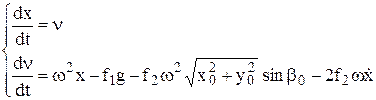 . (10.41)
. (10.41)
* * *
Разработана математическая модель движения частицы в процессе жиловки позволяет определить траекторию движения частицы при осуществлении жиловки. Инженерное решение данной модели позволяет найти оптимальную форму паза решетки для жиловки, по которому частица будет двигаться беспрепятственно.
Процесс смешивания и формования помадной массы на основе порошкообразного сахаро-паточного полуфабриката, модельные представления которого сформулированы Журавлевым А.А.
Визуализация гидродинамических потоков помадной массы при смешивании в смесителе с Z-образными месильными органами, позволила условно выделить в поперечном сечении области с различным деформационным поведением материала: валковый и коаксиальные зазоры и «жесткую» (застойную) зону (рис. 10.12).
В области валкового зазора А 1 А 4 В 4 В 1между месильными органами А и В происходит захват материала и постепенное его втягивание в зазор. Теоретические исследования и экспериментальная визуализация потоков показали, что вследствие различия скорости движения слоев материала, расположенных на разных расстояниях от поверхности месильных органов, в валковом зазоре существует зона отставания А 1 А 2 В 2 В 1 и зона опережения А 2 А 5 В 4 В 2(рис. 10.13).
 Рис. 10.13. Визуализация гидродинамических потоков помадной массы при смешивании в смесителе с Z-образными месильными органами.
Рис. 10.13. Визуализация гидродинамических потоков помадной массы при смешивании в смесителе с Z-образными месильными органами.
|
В зоне отставания скорость частиц материала по мере удаления от поверхности месильных органов постепенно уменьшается, а затем в некотором сечении хsхs меняет направление на противоположное, что приводит к возникновению противотока материала. В зоне опережения направление скорости движения частиц материала совпадает с направлением вращения месильных органов.
В области коаксиального зазора происходит вращательное движение слоев материала с постепенным уменьшением окружной скорости движения материала по мере удаления от поверхности месильного органа. В окрестности внутренней поверхности камеры смешивания на расстоянии Rа формируется слой толщиной (R 2 - R 0) в котором отсутствует течение материала.
В областях валкового и коаксиальных зазоров материал испытывает деформации сдвига, растяжения и сжатия, при этом отдельные слои движутся по разным линиям тока с различными скоростями, что приводит к их взаимной переориентации и смешиванию.
«Жесткие» (застойные) зоны возникают в слоях материала, прилегающих к внутренним стенкам корпуса смесителя и в слоях материала, находящихся на значительном удалении от месильных органов.
С целью аналитического исследования и моделирования деформационного поведения помадной массы при смешивании, рассмотрим течение сплошной среды в коаксиальном и валковом зазорах при следующих допущениях: движение среды установившееся, изотермическое и осесимметричное; среда несжимаема; инерционными и массовыми силами пренебрегаем.
Рассматривая деформационное поведение помадной массы в коаксиальном зазоре в виде задачи о течении вязко-пластичной среды между двумя коаксиальными цилиндрами, один из которых (внешний радиусом R 2 ) неподвижен, а другой (радиусом R 1 и длиной L) вращается с угловой скоростью w,уравнение движения и граничное условие в цилиндрических координатах имеет вид
 . (10.42)
. (10.42)
при r = R 1  , (10.43)
, (10.43)
где  - компоненты напряжения; r - текущий радиус, М - крутящий момент.
- компоненты напряжения; r - текущий радиус, М - крутящий момент.
С учетом реологического уравнения состояния вязко-пластичной среды
 (10.44)
(10.44)
и решения уравнения (10.42), имеем выражения для окружной скорости  материала в кольцевом зазоре для зоны поступательного течения (R 0 - R 1)
материала в кольцевом зазоре для зоны поступательного течения (R 0 - R 1)
 . (10.45)
. (10.45)
Полагая в выражении (10.45) r = R 1, определим угловую скорость w вращения цилиндра
 . (10.46)
. (10.46)
После ряда преобразований, уравнение (10.46) представим в следующем виде
 , (10.47)
, (10.47)
где  ;
;  . (10.48)
. (10.48)
Полагая, что  , разложим lnb в ряд Тейлора в окрестности единицы. Отбрасывая члены выше второго порядка, после ряда преобразований, уравнение (10.48) приводим к квадратному уравнению, решая которое относительно b, находим корень, удовлетворяющий условию
, разложим lnb в ряд Тейлора в окрестности единицы. Отбрасывая члены выше второго порядка, после ряда преобразований, уравнение (10.48) приводим к квадратному уравнению, решая которое относительно b, находим корень, удовлетворяющий условию 
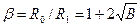 . (10.49)
. (10.49)
Окончательно имеем выражение для определения радиуса жесткой зоны R 0
 . (10.50)
. (10.50)
Последнее выражение позволяет определить условие распространения течения на весь коаксиальный зазор шириной (R 2 - R 1 ) без возникновения «жесткой» зоны. Полагая, что R 2= R 0,из выражения (10.50) имеем
 . (10.51)
. (10.51)
Рассматривая деформационное поведение помадной массы в валковом зазоре в виде задачи о течении неньютоновской среды между двумя валками радиусом R 1, вращающимися навстречу друг другу с окружной скоростью U,полагая течение в зазоре одномерным, уравнение движения в прямоугольных координатах имеет вид
 , (10.52)
, (10.52)
где dР/dх - градиент давления; h эф - эффективная вязкость помадной массы;  - компонента скорости по оси х.
- компонента скорости по оси х.
Принимая гипотезу прилипания, имеем граничные условия
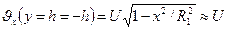 ;
;  , (10.53)
, (10.53)
где у - текущая координата по оси абсцисс; h - расстояние от оси симметрии до поверхности валка в произвольном сечении; Р (х 1)- давление в области входа (сечение х 1 х 1); Р (-х 2)- давление в области выхода (сечение ‑ х 2 ‑х 2).
Интегрируя выражение (10.34), с учетом условия прилипания (10.53), получим выражение для определения скорости материала  в валковом зазоре
в валковом зазоре
 . (10.54)
. (10.54)
Объемный расход через единицу ширины зазора
 , (10.55)
, (10.55)
В сечении - х 2, согласно условию (10.53), dР/dx = 0 и  = U. Расход в этом сечении по выражению (10.55) равен Q = 2 Uh 2.
= U. Расход в этом сечении по выражению (10.55) равен Q = 2 Uh 2.
В силу условия постоянства расхода в любом сечении из (10.55) имеем
 . (10.56)
. (10.56)
С учетом последнего равенства представим выражение (10.54) как
 . (10.57)
. (10.57)
Граничное значение области циркуляционного течения хs, в которой в центральной части потока скорость направлена в сторону, противоположную направлению движения валков, определим из уравнения (10.57), положив  = 0при у = 0. После ряда преобразований получим
= 0при у = 0. После ряда преобразований получим
 . (10.58)
. (10.58)
Как видно из выражения (10.40), положение границы области циркуляционного течения хs определяется положением сечения выхода - х 2,величиной межвалкового зазора h 0и лежит в интервале 0 < хs < х 1.Подставляя в это неравенство значение хs,получим ограничение, накладываемое на величину межвалкового зазора h 0,при котором существует циркуляционное течение в зазоре
 , (10.59)
, (10.59)
которое справедливо при условии 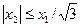 .
.
В соответствии с положениями теории ламинарного смешивания Спенсера и Мора, качество смешивания при однократном прохождении материала через область деформации можно оценить по величине средней деформации сдвига.
Для коаксиального зазора деформация сдвига, которой подвергается элементарный объем, поворачиваясь на угол  за время
за время  , определяется выражением
, определяется выражением
 , (10.60)
, (10.60)
которое после интегрирования и ряда преобразований дает выражение
 . (10.61)
. (10.61)
Средняя деформация сдвига, которой подвергается удельный объем материала при однократном проходе через коаксиальный зазор, равна
 , (10.62)
, (10.62)
где Q - объемный расход материала через коаксиальный зазор.
После подстановки в (10.62) значения определенного интеграла, получим
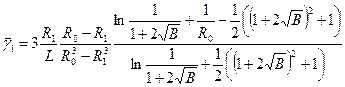 . (10.63)
. (10.63)
Для вычисления средней деформации сдвига, которой подвергается удельный объем материала, при однократном проходе через валковый зазор, воспользуемся выражением, полученным Р.В. Торнером
 , (10.64)
, (10.64)
где 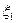 ,
,  - безразмерные координаты сечения входа и выхода, определяемые при значениях координат сечений входа и выхода х1, и х2 как
- безразмерные координаты сечения входа и выхода, определяемые при значениях координат сечений входа и выхода х1, и х2 как 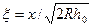 .
.
Суммарная удельная деформация сдвига 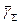 , которой подвергается материал за время смешивания tсм, равна произведению среднего арифметического значения деформаций за один проход через коаксиальный и валковый зазоры на число проходов
, которой подвергается материал за время смешивания tсм, равна произведению среднего арифметического значения деформаций за один проход через коаксиальный и валковый зазоры на число проходов
 . (10.65)
. (10.65)
Используя известное выражение для минимальной деформации сдвига  , обеспечивающей необходимое качество смешивания (индекс смешивания I)
, обеспечивающей необходимое качество смешивания (индекс смешивания I)
 (10.66)
(10.66)
и выражение (10.64), можно записать уравнение
 , (10.67)
, (10.67)
где η1 и η2 - вязкости дисперсионной среды и дисперсной фазы, соответственно, q - относительное содержание ключевого компонента в отобранной пробе.
Решая уравнение (10.67) численным методом, можно определить геометрические параметры смесителя или частоту вращения месильных органов n, обеспечивающих заданное качество смешивания (индекс смешивания I).
* * *
Аналитически рассмотрено течение вязко-пластичной помадной массы по формующим каналам круглого сечения - цилиндрическому, коническому, криволинейному коническому каналам и цилиндрическим каналам с коническим и криволинейным коническим входными участками. Для описания ламинарного стационарного стабилизированного и изотермического течения использовали "укороченное" уравнение Букингема. Получены приближенные выражения для определения давления, которое должен создавать нагнетатель для продавливания вязко-пластичной среды через формующие каналы с переменной по длине площадью поперечного сечения.
Рассмотрен механизм возникновения пульсаций давления, развиваемого шнековым нагнетателем при выпрессовывании конфетных масс. Аналитически установлено влияние геометрических и кинематических характеристик нагнетателя на величину амплитуды пульсаций давления; показано, что колебания давления во времени имеют вид пилообразной функции с периодом Тп = 1/N, где N- частота вращения шнека.
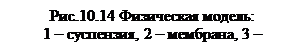
 Процесс фильтрования суспензии в канале с пористыми стенками, модельные представления которого сформулированы Потаповым А.И.
Процесс фильтрования суспензии в канале с пористыми стенками, модельные представления которого сформулированы Потаповым А.И.
Имеется суспензия, т.е. композиция из жидкости и содержащейся в ней твердой фазы полидисперсных частиц с произвольной функцией плотности распределениях их по размерам. Необходимо осуществить процесс очистки суспензии от присутствия твердой фазы. Схематически процесс очистки осуществляется следующим образом (рис. 10.14). Суспензия 1 подается в канал со скоростью  . Будем считать, что частицы в канале движутся без проскальзывания, что справедливо, если плотности несущей среды и частиц не слишком отличаются друг от друга. Обычно гидродинамический режим течения является турбулентным и поэтому в достаточно узких каналах турбулентные пульсации по масштабу соизмеримы с характерным гидравлическим диаметром поперечного сечения. Это означает, что в поперечном сечении происходит интенсивное перемешивание и следовательно, имея в виду, что профиль турбулентного течения имеет ярко выраженный пограничный слой с резким падением скорости и ядро с практически постоянной скоростью, можно считать гидродинамическую структуру близкой к идеальному перемешиванию в поперечном направлении и близкой идеальному вытеснению в продольном направлении по течению. Такая картина переноса суспензии в канале позволяет корректным образом пренебречь гравитационной составляющей твердой фазы на нижнюю стенку. Далее часть потока продолжает движение по каналу, а часть 3 фильтруется через пористую стенку 2, в том числе вместе с мелкодисперсной частью фильтрата. Физическая постановка позволяет перейти к математической идеализации, а именно, считать задачу осесимметричной и однонаправленной и поэтому одномерной.
. Будем считать, что частицы в канале движутся без проскальзывания, что справедливо, если плотности несущей среды и частиц не слишком отличаются друг от друга. Обычно гидродинамический режим течения является турбулентным и поэтому в достаточно узких каналах турбулентные пульсации по масштабу соизмеримы с характерным гидравлическим диаметром поперечного сечения. Это означает, что в поперечном сечении происходит интенсивное перемешивание и следовательно, имея в виду, что профиль турбулентного течения имеет ярко выраженный пограничный слой с резким падением скорости и ядро с практически постоянной скоростью, можно считать гидродинамическую структуру близкой к идеальному перемешиванию в поперечном направлении и близкой идеальному вытеснению в продольном направлении по течению. Такая картина переноса суспензии в канале позволяет корректным образом пренебречь гравитационной составляющей твердой фазы на нижнюю стенку. Далее часть потока продолжает движение по каналу, а часть 3 фильтруется через пористую стенку 2, в том числе вместе с мелкодисперсной частью фильтрата. Физическая постановка позволяет перейти к математической идеализации, а именно, считать задачу осесимметричной и однонаправленной и поэтому одномерной.
Физическая постановка задачи позволяет, в соответствии с принятыми допущениями, приступить к этапу синтеза математической модели. Для этого выделим элементарный объем и запишем для него дифференциальное уравнение материального баланса. Итак, массовый расход жидкости с плотностью  , входящий через площадь поперечного сечения элементарного объема
, входящий через площадь поперечного сечения элементарного объема  со скоростью
со скоростью  есть
есть

|
|
|



 Рис. 10.6. Схема сепарирующего органа (а) и технологического процесса разделения зерносмеси (б)
Рис. 10.6. Схема сепарирующего органа (а) и технологического процесса разделения зерносмеси (б)
 Рис. 10.7. Схема послойного движения зерносмеси
Рис. 10.7. Схема послойного движения зерносмеси
 , при котором происходит послойное движение сыпучего тела по всей его толщине и ширине кольцевого канала. Поскольку скорость элементарного слоя п (рис. 10.7, б, проекция сечения сыпучего тела в плоскости KZ) больше, чем вышележащего слоя (п - 1), и меньше, чем скорость нижележащего (п + 1), то сила трения
, при котором происходит послойное движение сыпучего тела по всей его толщине и ширине кольцевого канала. Поскольку скорость элементарного слоя п (рис. 10.7, б, проекция сечения сыпучего тела в плоскости KZ) больше, чем вышележащего слоя (п - 1), и меньше, чем скорость нижележащего (п + 1), то сила трения  со стороны вышележащего слоя препятствует его движению, а сила трения
со стороны вышележащего слоя препятствует его движению, а сила трения  со стороны нижележащего слоя способствует его движению. Следовательно, разность этих сил трения должна быть уравновешена силой инерции dРu данного элемента объема в абсолютном движении. При этом пренебрегаем радиальным перемещением элемента объема за полпериода колебаний опорной поверхности.
со стороны нижележащего слоя способствует его движению. Следовательно, разность этих сил трения должна быть уравновешена силой инерции dРu данного элемента объема в абсолютном движении. При этом пренебрегаем радиальным перемещением элемента объема за полпериода колебаний опорной поверхности. , (10.5)
, (10.5) - тангенциальная сила инерции элемента объема в абсолютном движении, где
- тангенциальная сила инерции элемента объема в абсолютном движении, где  - абсолютное угловое ускорение слоя п;
- абсолютное угловое ускорение слоя п;  и
и  - силы трения со стороны смежных слоев, где
- силы трения со стороны смежных слоев, где 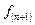 и
и 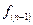 -коэффициенты сопротивления относительному сдвигу нижележащего (п + 1) и вышележащего (n - 1) слоев; G и dG - давления, соответственно вышележащей части зерносмеси и элемента объема, отнесенные на единицу площади опорной поверхности.
-коэффициенты сопротивления относительному сдвигу нижележащего (п + 1) и вышележащего (n - 1) слоев; G и dG - давления, соответственно вышележащей части зерносмеси и элемента объема, отнесенные на единицу площади опорной поверхности.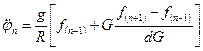 . (10.6)
. (10.6) .
. является возрастающей функцией силы тяжести G вышележащей части зерносмеси и зависимость
является возрастающей функцией силы тяжести G вышележащей части зерносмеси и зависимость  близка к линейной.
близка к линейной. и
и  , где f 0 - коэффициент сопротивления сдвигу слоя, расположенного на верхней свободной границе зерносмеси;
, где f 0 - коэффициент сопротивления сдвигу слоя, расположенного на верхней свободной границе зерносмеси;  и
и  - приращения коэффициентов сопротивления сдвигу соответственно слоев (n + 1) и (n - 1);
- приращения коэффициентов сопротивления сдвигу соответственно слоев (n + 1) и (n - 1);  - разность коэффициентов сопротивления сдвигу нижней и верхней границ зерносмеси; Gm - давление всей подвижной части зерносмеси на единицу площади опорной поверхности.
- разность коэффициентов сопротивления сдвигу нижней и верхней границ зерносмеси; Gm - давление всей подвижной части зерносмеси на единицу площади опорной поверхности. . (10.7)
. (10.7) . Введя безразмерные переменные
. Введя безразмерные переменные 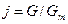 и
и  , позволяющие оценить интенсивность послойного движения зерносмеси через ее механические свойства, получим
, позволяющие оценить интенсивность послойного движения зерносмеси через ее механические свойства, получим . (10.8)
. (10.8) . В данном случае угловое ускорение опорной поверхности должно удовлетворить неравенству
. В данном случае угловое ускорение опорной поверхности должно удовлетворить неравенству 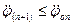 .Если
.Если  , то зерносмесь остается неподвижным относительно опорной поверхности. При постепенном увеличении углового ускорения опорной поверхности на радиусе R свое относительное движение начинают частицы, расположенные на верхней границе (j = 0) зерносмеси, при первом критическом значении углового ускорения
, то зерносмесь остается неподвижным относительно опорной поверхности. При постепенном увеличении углового ускорения опорной поверхности на радиусе R свое относительное движение начинают частицы, расположенные на верхней границе (j = 0) зерносмеси, при первом критическом значении углового ускорения 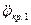 опорной поверхности, а затем движение постепенно распространяется в нижние слои. При достижении второго критического значения
опорной поверхности, а затем движение постепенно распространяется в нижние слои. При достижении второго критического значения  начинают относительное движение частицы, расположенные на нижней границе (j = 1) зерносмеси. В дальнейшем увеличении ускорения опорной поверхности (
начинают относительное движение частицы, расположенные на нижней границе (j = 1) зерносмеси. В дальнейшем увеличении ускорения опорной поверхности (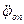 >>
>>  , где j0 и w - соответственно, угловые амплитуда и частота колебаний опорной поверхности, то можно представить критические значения ее угловой скорости
, где j0 и w - соответственно, угловые амплитуда и частота колебаний опорной поверхности, то можно представить критические значения ее угловой скорости , (10.9)
, (10.9) . (10.10)
. (10.10) , то для любой радиальной координаты R можно определить значение частоты колебаний w кр.2 кольцевого канала, при котором по всей толщине зерновой смеси будет протекать послойное движение, обусловливающее интенсивное самосортирование зерносмеси.
, то для любой радиальной координаты R можно определить значение частоты колебаний w кр.2 кольцевого канала, при котором по всей толщине зерновой смеси будет протекать послойное движение, обусловливающее интенсивное самосортирование зерносмеси. . (10.11)
. (10.11) . (10.12)
. (10.12) Рис. 10.8. Физическая модель процесса резания:
1 - крестовой нож; 2 - измельчаемое сырье; 3 - ножевая решетка;
F 1 - сила сопротивления перерезанию волокон сырья; F 2 - сила сопротивления перемешиванию; F 3 - силы трения между режущими плоскостями ножа и решетками; F 4 - усилие затяжки режущего механизма; F 5 - силы трения ножа и сырье; a - угол резания; Q - общее усилие резания; Q 1 - часть усилия, создаваемого подающим механизмом; Р 1, Р 2 - сопротивления проталкиванию сырья через отверстия решетки; w - угловая скорость вращения ножа.
Рис. 10.8. Физическая модель процесса резания:
1 - крестовой нож; 2 - измельчаемое сырье; 3 - ножевая решетка;
F 1 - сила сопротивления перерезанию волокон сырья; F 2 - сила сопротивления перемешиванию; F 3 - силы трения между режущими плоскостями ножа и решетками; F 4 - усилие затяжки режущего механизма; F 5 - силы трения ножа и сырье; a - угол резания; Q - общее усилие резания; Q 1 - часть усилия, создаваемого подающим механизмом; Р 1, Р 2 - сопротивления проталкиванию сырья через отверстия решетки; w - угловая скорость вращения ножа.
 , (10.13)
, (10.13) , (10.14)
, (10.14)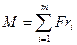 или
или  , (10.15)
, (10.15) . (10.16)
. (10.16) Рис. 10.9. Расчетная схема для определения сил сухого трения ножа о решетку:
АВD - один из четырех перьев серповидного ножа; ABC - равнобедренный треугольник, равный по площади АВD; r - произвольное расстояние от оси вращения до элементарной площадки ножа; l - длина узкой элементарной площадки; dr - ширина площадки; dF - сила трения действующая на элементарную площадку; р - давление ножа на часть решетки; v - скорость центра площадки; h - высота ножа от его основания (сторона квадрата); R - расстояние от вершины условного ножа до оси вращения; R 0 - радиус окружности в которую вписан четырехугольник.
Рис. 10.9. Расчетная схема для определения сил сухого трения ножа о решетку:
АВD - один из четырех перьев серповидного ножа; ABC - равнобедренный треугольник, равный по площади АВD; r - произвольное расстояние от оси вращения до элементарной площадки ножа; l - длина узкой элементарной площадки; dr - ширина площадки; dF - сила трения действующая на элементарную площадку; р - давление ножа на часть решетки; v - скорость центра площадки; h - высота ножа от его основания (сторона квадрата); R - расстояние от вершины условного ножа до оси вращения; R 0 - радиус окружности в которую вписан четырехугольник.
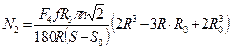 ,(10.17)
,(10.17) ; d 0 - диаметр отверстия; k - количество отверстий, перекрываемых одним ножом; S - площадь одного ножа; f - коэффициент трения скольжения ножа о металлическую часть решётки.
; d 0 - диаметр отверстия; k - количество отверстий, перекрываемых одним ножом; S - площадь одного ножа; f - коэффициент трения скольжения ножа о металлическую часть решётки.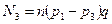 , или
, или , (10.18)
, (10.18) Рис. 10.10. Отверстие модифиванной решетки:
р 1 - давления на входе в канал; r 1 - расстояние вершин конуса, находящиеся на продолжении канала (для входного и выходного участка); р 2 - давление в наиболее узкой части канала; р 3 - давление на выходе из канала; q0 - половина угла раствора каждого из конусов; r 2 - расстояние от вершины каждого конуса до середины канала.
Рис. 10.10. Отверстие модифиванной решетки:
р 1 - давления на входе в канал; r 1 - расстояние вершин конуса, находящиеся на продолжении канала (для входного и выходного участка); р 2 - давление в наиболее узкой части канала; р 3 - давление на выходе из канала; q0 - половина угла раствора каждого из конусов; r 2 - расстояние от вершины каждого конуса до середины канала.
 Рис. 10.11. Наибольшее лобовое сечение одного ножа, вращающегося вокруг вертикальной оси:
w - угловая скорость вращения ножа; h - высота сечения ножа; dr - длина элементарной площадки; r - расстояние от оси вращения ножа до элементарной площадки; R - расстояние от оси вращения ножа до его конечной точки; dF - сила лобового сопротивления, действующая на элементарную площадку; v - скорость движения в элементарной площадки ножа; R 0 - радиус окружности на которую опирается каждое перо ножа
Рис. 10.11. Наибольшее лобовое сечение одного ножа, вращающегося вокруг вертикальной оси:
w - угловая скорость вращения ножа; h - высота сечения ножа; dr - длина элементарной площадки; r - расстояние от оси вращения ножа до элементарной площадки; R - расстояние от оси вращения ножа до его конечной точки; dF - сила лобового сопротивления, действующая на элементарную площадку; v - скорость движения в элементарной площадки ножа; R 0 - радиус окружности на которую опирается каждое перо ножа
 , (10.19)
, (10.19)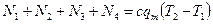 , (10.21)
, (10.21) - массовый расход продукта, откуда находим разность температур
- массовый расход продукта, откуда находим разность температур . (10.22)
. (10.22) . (10.23)
. (10.23) Рис. 10.12. Математическая модель
процесса жиловки
Рис. 10.12. Математическая модель
процесса жиловки
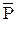 , нормальная реакция со стороны диска
, нормальная реакция со стороны диска  , нормальная реакция со стороны лопасти
, нормальная реакция со стороны лопасти  , соответствующие силы трения
, соответствующие силы трения 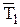 и
и  , а также переносная сила инерции
, а также переносная сила инерции  и кориолисова сила инерции
и кориолисова сила инерции 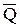 .
.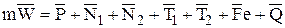 . (10.24)
. (10.24) , получим дифференциальное уравнение относительного движения системы в проекциях на эти оси
, получим дифференциальное уравнение относительного движения системы в проекциях на эти оси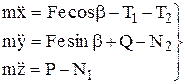 . (10.25)
. (10.25) ограничено поверхностью решетки, то равнодействующая сил равна нулю
ограничено поверхностью решетки, то равнодействующая сил равна нулю , (10.26)
, (10.26) (10.27)
(10.27) - масса частицы продукта, кг;
- масса частицы продукта, кг;  - ускорение свободного падения (
- ускорение свободного падения ( м/с2).
м/с2). также ограничено пером ножа и равнодействующая проекций сил действующих на частицу продукта в относительном движении, на ось
также ограничено пером ножа и равнодействующая проекций сил действующих на частицу продукта в относительном движении, на ось  . (10.28)
. (10.28) . (10.29)
. (10.29) (10.30)
(10.30)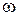 - угловая скорость вращения ротора, рад/с;
- угловая скорость вращения ротора, рад/с; 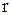 - радиус вращения частиц, м.
- радиус вращения частиц, м. , (10.31)
, (10.31) - относительная скорость частицы, м/с.
- относительная скорость частицы, м/с.
 (10.32)
(10.32) и угловой скорости вращения
и угловой скорости вращения  равен 90°, то уравнение (10.32) перепишется в виде
равен 90°, то уравнение (10.32) перепишется в виде . (10.33)
. (10.33) , (10.34)
, (10.34) , (10.35)
, (10.35)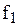 =
= 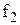 - соответственно коэффициенты трения продукта о поверхность решетки и перо ножа (для материалов мясо-сталь
- соответственно коэффициенты трения продукта о поверхность решетки и перо ножа (для материалов мясо-сталь  ).
).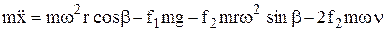 . (10.36)
. (10.36) . (10.37)
. (10.37) получим
получим . (10.38)
. (10.38) . (10.39)
. (10.39) . (10.40)
. (10.40)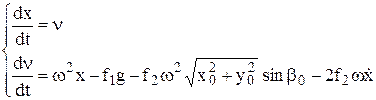 . (10.41)
. (10.41) Рис. 10.13. Визуализация гидродинамических потоков помадной массы при смешивании в смесителе с Z-образными месильными органами.
Рис. 10.13. Визуализация гидродинамических потоков помадной массы при смешивании в смесителе с Z-образными месильными органами.
 . (10.42)
. (10.42) , (10.43)
, (10.43) - компоненты напряжения; r - текущий радиус, М - крутящий момент.
- компоненты напряжения; r - текущий радиус, М - крутящий момент. (10.44)
(10.44) материала в кольцевом зазоре для зоны поступательного течения (R 0 - R 1)
материала в кольцевом зазоре для зоны поступательного течения (R 0 - R 1) . (10.45)
. (10.45) . (10.46)
. (10.46) , (10.47)
, (10.47) ;
;  . (10.48)
. (10.48) , разложим lnb в ряд Тейлора в окрестности единицы. Отбрасывая члены выше второго порядка, после ряда преобразований, уравнение (10.48) приводим к квадратному уравнению, решая которое относительно b, находим корень, удовлетворяющий условию
, разложим lnb в ряд Тейлора в окрестности единицы. Отбрасывая члены выше второго порядка, после ряда преобразований, уравнение (10.48) приводим к квадратному уравнению, решая которое относительно b, находим корень, удовлетворяющий условию 
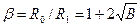 . (10.49)
. (10.49) . (10.50)
. (10.50) . (10.51)
. (10.51) , (10.52)
, (10.52) - компонента скорости по оси х.
- компонента скорости по оси х.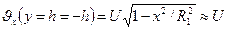 ;
;  , (10.53)
, (10.53) в валковом зазоре
в валковом зазоре . (10.54)
. (10.54) , (10.55)
, (10.55) . (10.56)
. (10.56) . (10.57)
. (10.57) . (10.58)
. (10.58) , (10.59)
, (10.59)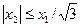 .
. за время
за время  , определяется выражением
, определяется выражением , (10.60)
, (10.60) . (10.61)
. (10.61) , (10.62)
, (10.62)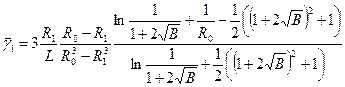 . (10.63)
. (10.63) , (10.64)
, (10.64)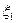 ,
,  - безразмерные координаты сечения входа и выхода, определяемые при значениях координат сечений входа и выхода х1, и х2 как
- безразмерные координаты сечения входа и выхода, определяемые при значениях координат сечений входа и выхода х1, и х2 как 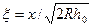 .
.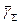 , которой подвергается материал за время смешивания tсм, равна произведению среднего арифметического значения деформаций за один проход через коаксиальный и валковый зазоры на число проходов
, которой подвергается материал за время смешивания tсм, равна произведению среднего арифметического значения деформаций за один проход через коаксиальный и валковый зазоры на число проходов . (10.65)
. (10.65) , обеспечивающей необходимое качество смешивания (индекс смешивания I)
, обеспечивающей необходимое качество смешивания (индекс смешивания I) (10.66)
(10.66) , (10.67)
, (10.67)
 Процесс фильтрования суспензии в канале с пористыми стенками, модельные представления которого сформулированы Потаповым А.И.
Процесс фильтрования суспензии в канале с пористыми стенками, модельные представления которого сформулированы Потаповым А.И. . Будем считать, что частицы в канале движутся без проскальзывания, что справедливо, если плотности несущей среды и частиц не слишком отличаются друг от друга. Обычно гидродинамический режим течения является турбулентным и поэтому в достаточно узких каналах турбулентные пульсации по масштабу соизмеримы с характерным гидравлическим диаметром поперечного сечения. Это означает, что в поперечном сечении происходит интенсивное перемешивание и следовательно, имея в виду, что профиль турбулентного течения имеет ярко выраженный пограничный слой с резким падением скорости и ядро с практически постоянной скоростью, можно считать гидродинамическую структуру близкой к идеальному перемешиванию в поперечном направлении и близкой идеальному вытеснению в продольном направлении по течению. Такая картина переноса суспензии в канале позволяет корректным образом пренебречь гравитационной составляющей твердой фазы на нижнюю стенку. Далее часть потока продолжает движение по каналу, а часть 3 фильтруется через пористую стенку 2, в том числе вместе с мелкодисперсной частью фильтрата. Физическая постановка позволяет перейти к математической идеализации, а именно, считать задачу осесимметричной и однонаправленной и поэтому одномерной.
. Будем считать, что частицы в канале движутся без проскальзывания, что справедливо, если плотности несущей среды и частиц не слишком отличаются друг от друга. Обычно гидродинамический режим течения является турбулентным и поэтому в достаточно узких каналах турбулентные пульсации по масштабу соизмеримы с характерным гидравлическим диаметром поперечного сечения. Это означает, что в поперечном сечении происходит интенсивное перемешивание и следовательно, имея в виду, что профиль турбулентного течения имеет ярко выраженный пограничный слой с резким падением скорости и ядро с практически постоянной скоростью, можно считать гидродинамическую структуру близкой к идеальному перемешиванию в поперечном направлении и близкой идеальному вытеснению в продольном направлении по течению. Такая картина переноса суспензии в канале позволяет корректным образом пренебречь гравитационной составляющей твердой фазы на нижнюю стенку. Далее часть потока продолжает движение по каналу, а часть 3 фильтруется через пористую стенку 2, в том числе вместе с мелкодисперсной частью фильтрата. Физическая постановка позволяет перейти к математической идеализации, а именно, считать задачу осесимметричной и однонаправленной и поэтому одномерной. , входящий через площадь поперечного сечения элементарного объема
, входящий через площадь поперечного сечения элементарного объема  со скоростью
со скоростью  есть
есть


