Для определения коэффициентов канонических уравнений метода перемещений необходимо построить эпюры моментов и поперечных сил в основной системе от приложенной нагрузки и от единичных смещений наложенных связей, пользуясь таблицей 16.1, приведенной в разделе 4 лекции 16, т.к. основная система представляет совокупность однопролетных статически неопределимых балок, для которых имеются заранее заготовленные решения. Для рассматриваемой рамы эти эпюры приведены на рис.17.5.
Реакции в наложенных связях от единичных смещений этих связей и от приложенной нагрузки r 1,1, r 1,2, r 1,3,..., R 1,Fнаходятся методом сечений.
Для определения реакций r 1,1 вырежем узел 1 в первом единичном состоянии и составим уравнения равновесия узла в виде суммы моментов всех сил относительно точки пересечения стержней, сходящихся в данном узле (см. рис. 17.6, а):
 .
.
Из полученного уравнения находим:
 .
.

Рис.17.5. Единичные и грузовая эпюры моментов для основной системы

Рис.17.6.К определению коэффициентов канонических уравнений метода перемещений: а – узел 1, б – узел 2, в – сечение I
Для определения r 2,1 вырежем узел 2 в первом единичном состоянии (см. рис. 17.6, б). Уравнение равновесия узла 2 имеет вид:
Из полученного уравнения находим:

Аналогичным образом находим остальные реакции, представляющие собой реактивные моменты в дополнительных заделках. Для определения реакции 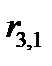 рассечем раму на две части, как показано на рис. 17.6, в, и составим уравнение равновесия верхней отсеченной части в виде суммы проекций всех сил на горизонтальную ось. Получим:
рассечем раму на две части, как показано на рис. 17.6, в, и составим уравнение равновесия верхней отсеченной части в виде суммы проекций всех сил на горизонтальную ось. Получим:
Отсюда:
Аналогичным образом определяются другие коэффициенты системы уравнений, представляющие собой реакции в дополнительном опорном стержне. После определения коэффициентов и решения системы канонических уравнений окончательная эпюра моментов может быть построена по формуле:
 . .
|
|
Дальнейший расчет проводится так же, как и при использовании метода сил.
ЛЕКЦИЯ 18. ПРИМЕР РАСЧЕТА РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Пусть требуется построить эпюры изгибающих моментов, поперечных и продольных сил для рамы, изображенной на рис.18.1, при F = 0,8 кН и EI =const.
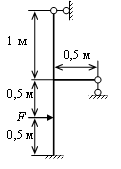


Рис.18.1. Заданная рама Рис.18.2. Шарнирно- Рис.18.2. Основная
стержневая модель система
Подсчитаем число неизвестных. Рама имеет один жесткий узел, следовательно  . Для определения числа линейных перемещений поставим шарниры во все узлы, считая опорные, как показано на рис.18.2. Степень свободы полученной шарнирно-стержневой системы равна 2У-С-Со= 2×4-3-4=1. Следовательно, число независимых линейных смещений равно
. Для определения числа линейных перемещений поставим шарниры во все узлы, считая опорные, как показано на рис.18.2. Степень свободы полученной шарнирно-стержневой системы равна 2У-С-Со= 2×4-3-4=1. Следовательно, число независимых линейных смещений равно 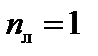 . Общее число неизвестных метода перемещений:
. Общее число неизвестных метода перемещений:
 .
.
Основную систему метода перемещений получим, наложив связь, препятствующую угловому перемещению узла 1 и линейному перемещению узлов 1 и 2 по горизонтали. Основная система показана на рис.18.3.
Канонические уравнения метода перемещений для рассчитываемой рамыимеют вид:

|
(18.1)
|
Для определения коэффициентов канонических уравнений построим эпюры изгибающих моментов от единичных перемещений в направлении наложенных связей и от приложенной нагрузки для основной системы (рис.18.4). Эпюры строятся с помощью данных, приведенных в разделе 4 лекции 16(см. табл.16.1).

Рис.18.4. К определению коэффициентов канонических уравнений метода перемещений
Коэффициенты канонических уравнений найдем статическим способом. Для определения коэффициента  вырежем узел 1 в первом единичном состоянии (рис.18.5, а) и составим для этого узла уравнения равновесия в виде суммы моментов. Получим:
вырежем узел 1 в первом единичном состоянии (рис.18.5, а) и составим для этого узла уравнения равновесия в виде суммы моментов. Получим:
отсюда 
 Рис.18.5. К определению коэффициентов канонических уравнений метода перемещений: а – узел 1 в первом единичном состоянии, б - узел 1 во втором единичном состоянии, в - узел 1 в грузовом состоянии
Рис.18.5. К определению коэффициентов канонических уравнений метода перемещений: а – узел 1 в первом единичном состоянии, б - узел 1 во втором единичном состоянии, в - узел 1 в грузовом состоянии
Последовательно вырезая узел 1 во втором единичном и грузовом состояниях (рис.18.5,б,в) и составляя для этого узла уравнения равновесия в виде суммы моментов, получаем:
 .
.
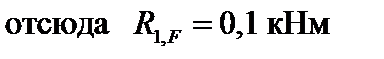
Для определения коэффициентов второй строки, представляющих собой реакции в дополнительном горизонтальном опорном стержне, воспользуемся круговым разрезом 1, показанным на рис.18.6. Для отсеченной части, изображенной на рис. 18.6, составим уравнения равновесия в виде суммы проекций всех сил на горизонтальную ось в единичных (рис. 18.6, а, б) и грузовом (рис. 18.6, в) состояниях.
 Рис.18.6. К определению коэффициентов канонических уравнений метода перемещений: а – круговое сечение I в первом единичном состоянии, б - круговое сечение I во втором единичном состоянии, в - круговое сечение I в грузовом состоянии
Рис.18.6. К определению коэффициентов канонических уравнений метода перемещений: а – круговое сечение I в первом единичном состоянии, б - круговое сечение I во втором единичном состоянии, в - круговое сечение I в грузовом состоянии
Получим:
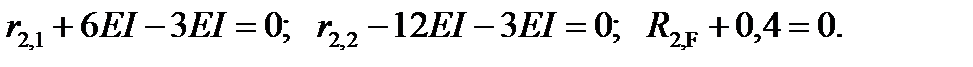
| (18.2)
|
Решая уравнения (18.2), находим:
Подставим найденные значения коэффициентов в канонические уравнения метода перемещений(18.1) и решим их:
Окончательную эпюру моментов для заданной рамы построим по формуле:
Чтобы воспользоваться этой формулой, предварительно построим эпюры  . Эти две эпюры и окончательная эпюра моментов показаны на рис.18.7.
. Эти две эпюры и окончательная эпюра моментов показаны на рис.18.7.

Рис.18.7. Исправленные ( ,
, 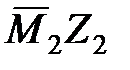 ) и окончательная (М) эпюры моментов
) и окончательная (М) эпюры моментов
Поперечные силы в стержнях рамы можно найти по эпюре изгибающих моментов на основании дифференциальной зависимости  . Так как эпюра изгибающих моментов состоит из отрезков прямых, то поперечная сила на каждом участке рамы находится как тангенс угла наклона огибающей эпюры моментов. Эпюра поперечных сил показана на рис.18.8.
. Так как эпюра изгибающих моментов состоит из отрезков прямых, то поперечная сила на каждом участке рамы находится как тангенс угла наклона огибающей эпюры моментов. Эпюра поперечных сил показана на рис.18.8.

Рис.18.8. Эпюра поперечных сил

а б
Рис.18.9. К проверке результатов решения: а – проверка равновесия моментов в узле 1, б – проверка равновесия кругового сечения I
Для проверки правильности построения эпюр М и Q проверим равновесие рамы. Вырежем узел 1 и приложим к нему моменты, действующие на этот узел со стороны отброшенных стержней (рис.18.9, а). Значения моментов определяем по эпюре М (рис.18.7). Найдем сумму моментов в данном узле. Получим:

Таким образом, неуравновешенный момент в узле 1 составляет 0,00024кНм. Абсолютное значение погрешности не позволяет судить о точности результатов, поэтому вычислим относительную погрешность ε:

Как видим, относительная погрешность определения изгибающих моментов мала, возникновение же ее объясняется тем обстоятельством, что при выполнении расчетов все результаты округлялись на третьей значащей цифре.
Аналогичным образом проверяется равновесие по поперечным силам. Проведем круговое сечение, как показано на рис.18.9,б, приложим поперечные силы, действующие на узел со стороны отброшенных стержней и вычислим сумму проекций всех сил на горизонтальную ось, обозначив последнюю буквой х. Получим:

Относительная погрешность составляет 
ЛЕКЦИЯ 19. ПРИМЕР РАСЧЕТА РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ
Для рамы, изображенной на рис.19.1, построить эпюры изгибающих моментов, поперечных и продольных сил.
Дано: 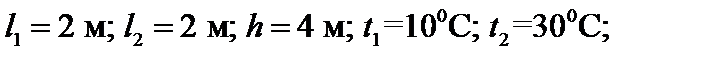


Рис.19.1. Заданная рама
Решение:
1. Определение числа неизвестных:

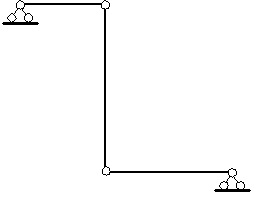
Рис.19.2. Шарнирно-стержневая модель рамы
Для определения числа независимых линейных перемещений  ставим шарниры во все узлы, включая опорные (рис.19.2), и определяем степень свободы полученной шарнирно-стержневой системы.
ставим шарниры во все узлы, включая опорные (рис.19.2), и определяем степень свободы полученной шарнирно-стержневой системы.

следовательно,  = 1.
= 1.
2. Образуем основную систему.
Основная система образуется постановкой дополнительных связей в узлы рамы (см. рис.19.3)
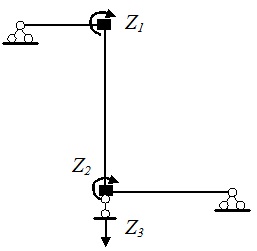
Рис.19.3. Основная система
3. Составляем канонические уравнения метода перемещений
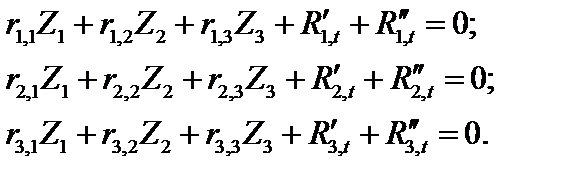
4.Определение коэффициентов канонических уравнений:
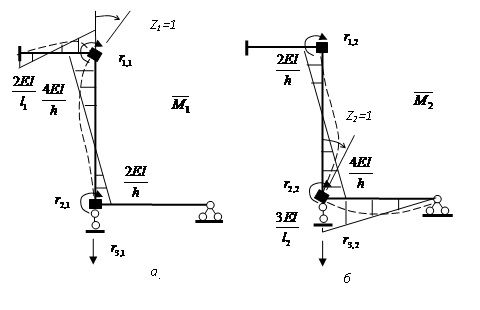
Рис.19.4. Единичные эпюры моментов: а – первая единичная эпюра, б –вторая единичная эпюра
4.1) Построение эпюры  (рис.19.4,а; строится с помощью таблицы 16.1);
(рис.19.4,а; строится с помощью таблицы 16.1);
4.2) Построение эпюры
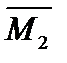
(рис.19.4,б;строится с помощью таблицы 16.1);
4.3) Построение эпюры  (рис.19.5, а;строится с помощью таблицы 16.1);
(рис.19.5, а;строится с помощью таблицы 16.1);

Рис.19.5. Третья единичная эпюра (а) и перемещения узлов при равномерном нагреве (б)
4.4) Построение эпюр изгибающих моментов от температурного воздействия для основной системы.
Температурное воздействие (рис.19.6, б) представим в виде суммы равномерного нагрева с постоянной по высоте сечения температурой  (рис.19.6, в) и неравномерного нагрева с нулевой температурой на оси и температурой наружных волокон
(рис.19.6, в) и неравномерного нагрева с нулевой температурой на оси и температурой наружных волокон  где
где  , как показано на рис.19.6, г. Предполагается, что сечение имеет прямоугольную форму (рис.19,6, а).
, как показано на рис.19.6, г. Предполагается, что сечение имеет прямоугольную форму (рис.19,6, а).

Рис.19.6. Поперечное сечение и эпюра температур: а – прямоугольное сечения, б - эпюра температур по высоте сечения, в –равномерный нагрев, г – неравномерный нагрев
Отдельно строим эпюры изгибающих моментов от равномерного и неравномерного нагрева. Для построения эпюры моментов от равномерного нагрева предварительно найдем температурные удлинения стержней по формуле 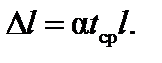 В нашем случае
В нашем случае  . Получаем:
. Получаем:

Перемещения узлов основной системы от равномерного нагрева показаны на рис.19.5,б. Зная абсолютные перемещения узлов, можно найти взаимные поперечные перемещения концов стержней. Взаимное поперечное перемещение концов стержня 1-3 равно  , взаимное поперечное перемещение концов стержня 1-2 равно
, взаимное поперечное перемещение концов стержня 1-2 равно 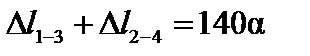 , взаимное поперечное перемещение концов стержня 2-4 равно нулю. Эпюру изгибающих моментов от равномерного нагрева построим, используя таблицы моментов от единичных перемещений и умножая эти эпюры на найденные взаимные перемещения концов стержней. Эта эпюра приведена на рис.19.7, а.
, взаимное поперечное перемещение концов стержня 2-4 равно нулю. Эпюру изгибающих моментов от равномерного нагрева построим, используя таблицы моментов от единичных перемещений и умножая эти эпюры на найденные взаимные перемещения концов стержней. Эта эпюра приведена на рис.19.7, а.
Эпюра изгибающих моментов от неравномерного нагрева строится непосредственно с помощью таблиц. Эта эпюра приведена на рис.19.7,б.
4.5) По построенным эпюрам моментов статическим способом находим коэффициенты канонических уравнений.
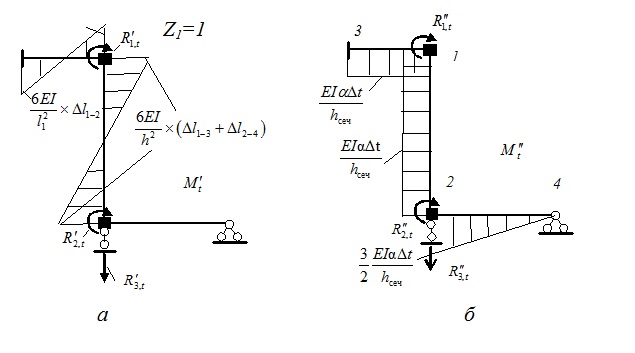
Рис.19.7.Эпюры изгибающих моментов от: а – равномерного нагрева, б – от неравномерного нагрева
Для определения коэффициента  вырежем узел 1 в состоянии
вырежем узел 1 в состоянии  (см.рис.19.8,а) и составим для него уравнение равновесия в виде суммы моментов. Получим:
(см.рис.19.8,а) и составим для него уравнение равновесия в виде суммы моментов. Получим:  Отсюда
Отсюда 
Для определения коэффициента  вырежем
вырежем 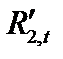 узел 2 в состоянии
узел 2 в состоянии  (см.рис.19.8,б) и составим для него уравнение равновесия в виде суммы моментов. Получим:
(см.рис.19.8,б) и составим для него уравнение равновесия в виде суммы моментов. Получим:  Отсюда
Отсюда 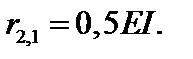

Рис.19.8. К определению коэффициентов канонических уравнений: а –узел 1 в первом единичном состоянии, узел 2 в первом единичном состоянии, круговое сечение I в первом единичном состоянии
Для определения коэффициента  проведем круговое сечение I состоянии
проведем круговое сечение I состоянии  (рис.19.8,а), выпишем из таблицы 16.1 значения поперечных сил в стержнях и составим уравнение равновесия отсеченной части в виде суммы проекций всех сил на ось У.
(рис.19.8,а), выпишем из таблицы 16.1 значения поперечных сил в стержнях и составим уравнение равновесия отсеченной части в виде суммы проекций всех сил на ось У.
Получим: 
Отсюда 
Отметим, что найти реакцию  из условия равновесия узла 2 невозможно, так как неизвестна продольная сила в стержне 1-2.
из условия равновесия узла 2 невозможно, так как неизвестна продольная сила в стержне 1-2.
Аналогичным образом находятся остальные коэффициенты канонических уравнений. Эти коэффициенты, представляющие реакции в наложенных связях от различных воздействий, показаны на рис.19.4, 19.5 и 19.7, а методика их вычисления изложена выше.
Приводим значения коэффициентов (читателю рекомендуется найти их самостоятельно):



5) Решение системы канонических уравнений.
После подстановки найденных значений коэффициентов в систему канонических уравнений и сокращения всех членов этих уравнений на EI получаем:

Решая систему уравнений, находим:

6) Построение окончательной эпюры моментов
Окончательную эпюру моментов строим по формуле:

Предварительно строим исправленные эпюры моментов 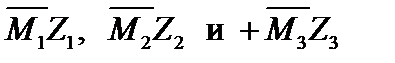 (см. рис.19.9).
(см. рис.19.9).

Рис.19.9. Исправленные эпюры моментов
Окончательная эпюра моментов приведена на рис.19.10,а. Там же показаны эпюры поперечных (рис.19.10, б) и продольных (рис.19.10, в) сил.
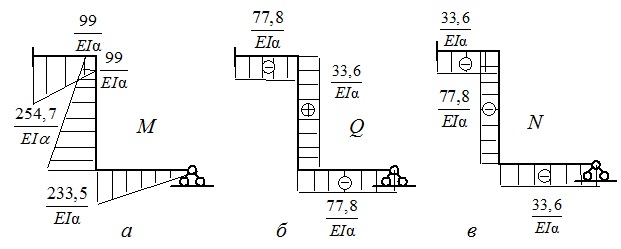
Рис.19.10. Окончательные эпюры: а – изгибающих моментов, б - поперечных сил, в – продольных сил
7) Проверка правильности построенных эпюр.
Чтобы удостовериться в правильности построенных эпюр, проверим равновесие моментов в узлах 1 и 2 и равновесие поперечных сил в круговом сечении I. Как видно из рисунков 19.11, а,б и в, равновесие как моментов, так и поперечных сил соблюдается полностью. Следовательно, полученные результаты верны.
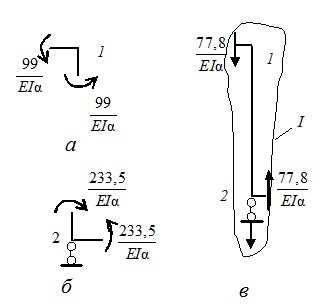
Рис.19.11. Проверка равновесия: а – по моментам в узле 1, б - по моментам в узле 2, в - по поперечным силам в сечении I



 .
. .
.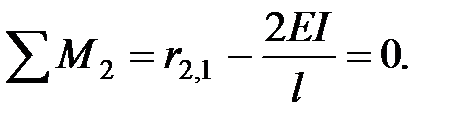

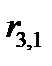 рассечем раму на две части, как показано на рис. 17.6, в, и составим уравнение равновесия верхней отсеченной части в виде суммы проекций всех сил на горизонтальную ось. Получим:
рассечем раму на две части, как показано на рис. 17.6, в, и составим уравнение равновесия верхней отсеченной части в виде суммы проекций всех сил на горизонтальную ось. Получим:

 .
.



 . Для определения числа линейных перемещений поставим шарниры во все узлы, считая опорные, как показано на рис.18.2. Степень свободы полученной шарнирно-стержневой системы равна 2У-С-Со= 2×4-3-4=1. Следовательно, число независимых линейных смещений равно
. Для определения числа линейных перемещений поставим шарниры во все узлы, считая опорные, как показано на рис.18.2. Степень свободы полученной шарнирно-стержневой системы равна 2У-С-Со= 2×4-3-4=1. Следовательно, число независимых линейных смещений равно 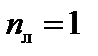 . Общее число неизвестных метода перемещений:
. Общее число неизвестных метода перемещений: .
.

 вырежем узел 1 в первом единичном состоянии (рис.18.5, а) и составим для этого узла уравнения равновесия в виде суммы моментов. Получим:
вырежем узел 1 в первом единичном состоянии (рис.18.5, а) и составим для этого узла уравнения равновесия в виде суммы моментов. Получим:


 .
.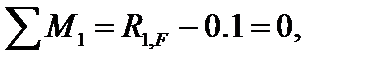
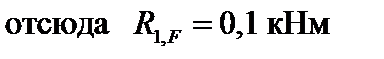
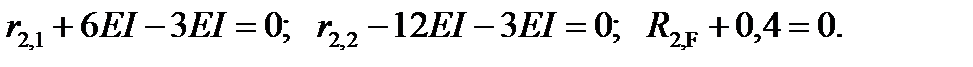




 . Эти две эпюры и окончательная эпюра моментов показаны на рис.18.7.
. Эти две эпюры и окончательная эпюра моментов показаны на рис.18.7.
 ,
, 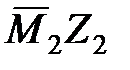 ) и окончательная (М) эпюры моментов
) и окончательная (М) эпюры моментов . Так как эпюра изгибающих моментов состоит из отрезков прямых, то поперечная сила на каждом участке рамы находится как тангенс угла наклона огибающей эпюры моментов. Эпюра поперечных сил показана на рис.18.8.
. Так как эпюра изгибающих моментов состоит из отрезков прямых, то поперечная сила на каждом участке рамы находится как тангенс угла наклона огибающей эпюры моментов. Эпюра поперечных сил показана на рис.18.8.





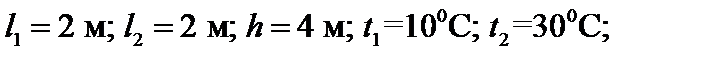




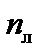 ставим шарниры во все узлы, включая опорные (рис.19.2), и определяем степень свободы полученной шарнирно-стержневой системы.
ставим шарниры во все узлы, включая опорные (рис.19.2), и определяем степень свободы полученной шарнирно-стержневой системы.
 = 1.
= 1.
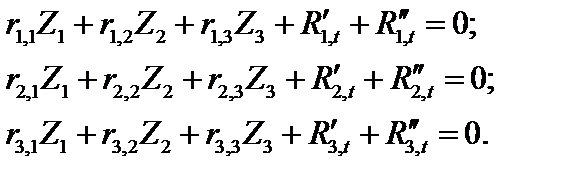

 (рис.19.4,а; строится с помощью таблицы 16.1);
(рис.19.4,а; строится с помощью таблицы 16.1);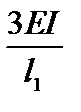
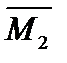 (рис.19.4,б;строится с помощью таблицы 16.1);
(рис.19.4,б;строится с помощью таблицы 16.1);
 (рис.19.5, а;строится с помощью таблицы 16.1);
(рис.19.5, а;строится с помощью таблицы 16.1);
 (рис.19.6, в) и неравномерного нагрева с нулевой температурой на оси и температурой наружных волокон
(рис.19.6, в) и неравномерного нагрева с нулевой температурой на оси и температурой наружных волокон  где
где  , как показано на рис.19.6, г. Предполагается, что сечение имеет прямоугольную форму (рис.19,6, а).
, как показано на рис.19.6, г. Предполагается, что сечение имеет прямоугольную форму (рис.19,6, а).
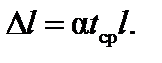 В нашем случае
В нашем случае  . Получаем:
. Получаем:
 , взаимное поперечное перемещение концов стержня 1-2 равно
, взаимное поперечное перемещение концов стержня 1-2 равно 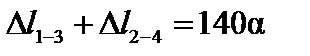 , взаимное поперечное перемещение концов стержня 2-4 равно нулю. Эпюру изгибающих моментов от равномерного нагрева построим, используя таблицы моментов от единичных перемещений и умножая эти эпюры на найденные взаимные перемещения концов стержней. Эта эпюра приведена на рис.19.7, а.
, взаимное поперечное перемещение концов стержня 2-4 равно нулю. Эпюру изгибающих моментов от равномерного нагрева построим, используя таблицы моментов от единичных перемещений и умножая эти эпюры на найденные взаимные перемещения концов стержней. Эта эпюра приведена на рис.19.7, а.
 вырежем узел 1 в состоянии
вырежем узел 1 в состоянии  (см.рис.19.8,а) и составим для него уравнение равновесия в виде суммы моментов. Получим:
(см.рис.19.8,а) и составим для него уравнение равновесия в виде суммы моментов. Получим:  Отсюда
Отсюда 
 вырежем
вырежем 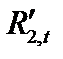 узел 2 в состоянии
узел 2 в состоянии  Отсюда
Отсюда 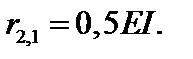

 проведем круговое сечение I состоянии
проведем круговое сечение I состоянии 







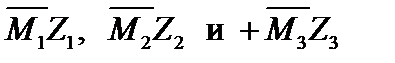 (см. рис.19.9).
(см. рис.19.9).




