Тема урока: Сочетательное свойство сложение (Математика, 2 класс, Часть 1. Стр 44-45)

Этап работы Деятельность учителя Деятельность учащихся Этап ознакомления с новым материалом Ребята, на партах у вас приготовлены геометрические фигуры. Выложите сначала 3 ромба, далее 4 круга и 6 треугольников . - Сколько фигур выложили? - Как их удобнее сосчитать? 3 + 4+ 6 записываю на доске Вывод: эту сумму можно посчитать разными способами. - Чему мы будем учиться?   Задание 1, выполняем вместе и комментируем. Читаем, определяем суть задания. - Чем похожи все выражения? - Чем отличаются? - Какое свойство применили?   Вывод: результат сложения не изменится, если поменять слагаемые местами. - Это свойство называют переместительным, так как мы меняли числа местами.   Вычислите значение выражения: 6+ 7 + 8 + 9 + 3 + 2 + 1 + 4 = Почему трудно выполнить задание? Чтобы было легче складывать , есть еще одно свойство. Прочитайте в учебнике.     В математике – это свойство называют сочетательным. Эти два свойства можно использовать вместе. Дети берут и выкладывают. 13   Сначала 6+4,а потом еще+3     Складывать числа в том порядке, который нам нравится порядке.   Выполняют задание, проговаривая действия сложения. - Поставим в скобки. - Одинаковые. - Соседние слагаемые заменили их суммой.   Неудобно складывать.   Результат сложения не изменится, если соседние слагаемые заменить их суммой. Этап его первичного закрепления. Как же мы решим с вами наше выражение? 6+ 7 + 8 + 9 + 3 + 2 + 1 + 4 = Объясните как вы будете вычислять, используя оба свойства сложения. ( в любом порядке, как удобнее). Почему так объединяли? На листочках записано выражение: 14 + 15+ 6 +5 вычислите, используя оба свойства. Вычислите, работая в парах, а потом проверим. Что помогло быстро найти значение выражения? (6+4) +(7+3) + (8+2) + (9+1) = Чтобы получить круглое число. Работают в парах. (14+6) + (15+5)=40 Перестановка слагаемых и замена слагаемых суммой.

 

3. В какой последовательности изучают вычислительные приемы сложения и вычитания в пределах 100 по программе М.И. Моро. Укажите теоретическую основу каждого приема.

Случаи (выражения) сложения и вычитания:

1.Однозначных и двузначных чисел без перехода через разряд (25+3 и 25-3)

2.Однозначных и двузначных чисел с переходом через разряд (37+5 и 32-7)

3.Двух двузначных чисел без перехода через разряд (64-21и 64+21)

4.Двух двузначных чисел с переходом через разряд (28+54 и 62- 36)

Все эти случаи рассматривают по всем программам, но из каждого случая может быть выделен частный и поэтому уроков ознакомления с новыми случаями оказывается гораздо больше.

Теоретической основой всех этих случаев является:

1.Знание разрядного состава двузначных чисел;

2.Знание законов сложения (переместительного и сочетательного) и вывода из них: к единицам удобнее прибавлять (вычитать) единицы, а к десяткам десятки. Этот вывод отражает принцип поразрядного сложения и вычитания чисел в пределах 100.

3.Знание таблиц сложения и вычитания в пределах 10 и 20.

 

 В разных учебниках математики предлагают разную последовательность изучения этих случаев. По программе М.И.Моро (2 кл,1ч., с.57) предлагается такая последовательность изучения приемов + и – в пределах 100:

1. В начале темы на подготовительном этапе повторяют случаи сложения и вычитания двузначных чисел, которые изучили еще в теме «Нумерация чисел в пределах 100».

Их т.о.-

· знание разрядного состава чисел

· соотношения между десятками и единицами

· случаи сложения и вычитания в пределах 10.

Это такие случае как:

50+30=80

5д+3д=8д

50-30=20

5д-3д=2д

2. 2-ой прием дан на стр.58 (Моро 2 кл. ч. 1) – прием сложения двузначного числа и разрядного без перехода через разряд.

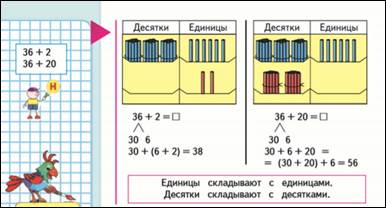
Это такие случаи:

36+2= 30+ 6+ 2= 30+(6+2)=38 –в основе сочетательный закон.

36+20= 30+6+20=(30+20)+6=56 – в основе переместительный и сочетательный законы.

На уроке делают вывод: к единицам удобнее прибавлять (вычитать) единицы, а к десяткам десятки.

Этот вывод отражает принцип поразрядного сложения и вычитания чисел в пределах 100.

3.3ий прием дан на стр. 59 - прием вычитания из двузначного неразрядного числа разрядного без перехода через разряд.

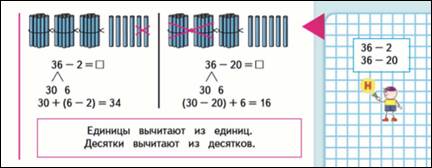
36-2= 30+(6-2)=34

36-20 = 30+6-20=(30-20)+6=16.

Действия сначала моделируют на палочках, а потом учитель сообщает, что десятки удобнее вычитать из десятков, а единицы из единиц.

4.4-ый этап на с.60 - частный случай прибавления к двузначным числам однозначных, когда в сумме получается круглое число.

26+4                            76+24

20+(6+4)=30               70+6+24=100

 Опираемся на 2-ой этап.

5.5-ый этап на с.61 – частный случай вычитания однозначного числа из круглого.

30-7=23

20+(10-7)=23                             

Мы знаем, что единицы вычитаются из единиц, но в числе 30 отдельных единиц нет (строим модель на палочках). Поэтому берем 1 пучок из 3-х, развязываем его и тогда 7 единиц вычитываем из 10 единиц. Получается 23.

30-7= 20+(10-7)=23

6.6ой этап на стр.62 – частный случай вычитания двузначного числа из круглого.

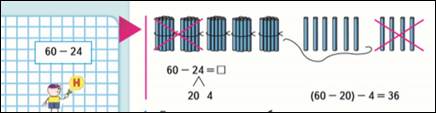
60-24=60-20-4=40-4=36

Сначала разбираем на палочках, опираясь на случай 30-7. Убираем 2 пучка по 10 палочек из 6, затем еще 1 развязываем и убираем 4 палочки из 10:

7.7-ой этап стр.66 - прием сложения двузначных и однозначных чисел с переходом через десяток.   

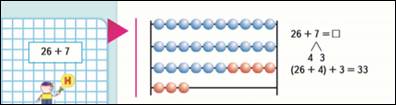
Используют прием прибавления по частям.

26+7=33             Опираемся на прием сложения двух однозначных чисел с

26+(4+3)=33       переходом через разряд.

8.8ой этап на стр. 67 - прием вычитания из двузначного числа однозначного с переходом через разряд.

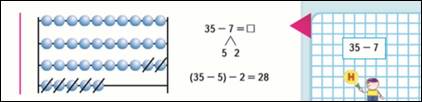
 Используют прием вычитания по частям.

35-7=28      Опираются на прием вычитания в пределах 20

(35-5)-2=28

9.9ый этап в учебнике М2М, 2ч., стр. 4 - прием сложения двузначного числа и двузначного без перехода через разряд.

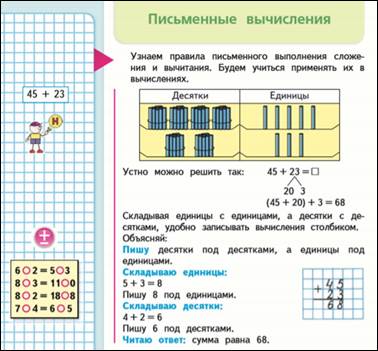
45+23=68

(45+20)+3=68

10.10ый этап в М2М, 2ч., стр. 5 - прием вычитания из двузначного числа двузначного без перехода через разряд.

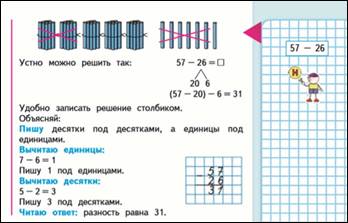
57-26=31

(57-20) -6=31

11.11ый этап. Далее следует рассмотреть прием сложения двузначного числа с двузначным с переходом через десяток, но в учебнике М2М, 2ч такой урок не предусмотрен. Следовательно, учитель включает этот прием в уроки самостоятельно на стр. 11-12.

45+28=73

(45+20)+8=73

12.12ый этап в М2М, 2ч. на стр.29 - прием вычитания из двузначного числа двузначного с переходом через разряд.

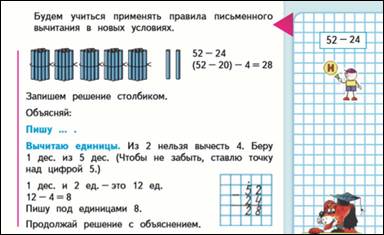
52-24=28

(52-20)-4=28

Таким образом, рассмотрены все случаи сложения и вычитания в пределах 100 и учащиеся должны понять:

1. Принцип поразрядного сложения и вычитания;

2. В процессе устных вычислений сначала прибавляют или вычитают более крупные разрядные единицы, т.е. десятки, а затем более мелкие – единицы. Это отличает устные приемы сложения и вычитания от письменных.

С каждым из названных приемов работают по плану:

1. повторение т.о. данного приема;

2.ознакомления с приемом с помощью наглядных пособий;

3.формирование умения использовать данный прием для вычислений (задания с подробным объяснением и записью);

4.формирование навыка (свернутость, автоматизм, быстрота, обобщенность действий).

Для формирования навыка требуется длительное время. В данной теме результаты не заучиваются, но выполнять действия ребенок должен научиться правильно и быстро. Поэтому в течение длительного времени на каждом уроке предлагаются:

- этапы устного счета (устные упражнения и игры);

- математические диктанты;

- дидактические игры;

- работа с карточками и т.д.          

 

4. Назовите этапы изучения любого вычислительного приема. Составьте фрагмент урока, включающий в себя три этапа (подготовительный, ознакомление, первичное закрепление), связанные с изучением приема сложения для случаев: 34+20 и 34+2. М2М, ч. 1, стр. 58. Используйте необходимые наглядные пособия.

Рассмотрим случаи (выражения) сложения и вычитания:

1.Однозначных и двузначных чисел без перехода через разряд (25+3 и 25-3)

2.Однозначных и двузначных чисел с переходом через разряд (37+5 и 32-7)

3. Двух двузначных чисел без перехода через разряд (64-21и 64+21)

4.Двух двузначных чисел с переходом через разряд (28+54 и 62- 36)

Все эти случаи рассматривают по всем программам, но из каждого случая может быть выделен частный и поэтому уроков ознакомления с новыми случаями оказывается гораздо больше.

Теоретической основой всех этих случаев является:

1.Знание разрядного состава двузначных чисел;

2.Знание законов сложения (переместительного и сочетательного) и вывода из них: к единицам удобнее прибавлять (вычитать) единицы, а к десяткам десятки. Этот вывод отражает принцип поразрядного сложения и вычитания чисел в пределах 100.

3.Знание таблиц сложения и вычитания в пределах 10 и 20.

В разных учебниках математики предлагают разную последовательность изучения этих случаев. По программе М.И.Моро (2 кл,1ч., с.57) предлагается такая последовательность изучения приемов + и – в пределах 100:

1. В начале темы на подготовительном этапе повторяют случаи сложения и вычитания двузначных чисел, которые изучили еще в теме «Нумерация чисел в пределах 100». Их т.о.- знание разрядного состава чисел, соотношения между десятками и единицами, случаи сложения и вычитания в пределах 10. Это такие случае как:

50+30=80

5д+3д=8д

50-30=20

5д-3д=2д

2. 2-ой прием дан на стр.58 (Моро 2 кл. ч. 1) – прием сложения двузначного числа и разрядного без перехода через разряд.

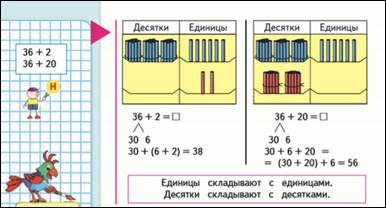
Это такие случаи:

36+2= 30+ 6+ 2= 30+(6+2)=38 –в основе сочетательный закон.

36+20= 30+6+20=(30+20)+6=56 – в основе переместительный и сочетательный законы.

На уроке делают вывод: к единицам удобнее прибавлять (вычитать) единицы, а к десяткам десятки.

Этот вывод отражает принцип поразрядного сложения и вычитания чисел в пределах 100.

3.3ий прием дан на стр. 59 - прием вычитания из двузначного неразрядного числа разрядного без перехода через разряд.

36-2= 30+(6-2)=34

36-20 = 30+6-20=(30-20)+6=16.

Действия сначала моделируют на палочках, а потом учитель сообщает, что десятки удобнее вычитать из десятков, а единицы из единиц.

4.4-ый этап на с.60 - частный случай прибавления к двузначным числам однозначных, когда в сумме получается круглое число.

26+4                            76+24

20+(6+4)=30               70+6+24=100

 Опираемся на 2-ой этап.

5.5-ый этап на с.61 – частный случай вычитания однозначного числа из круглого.

30-7=23

20+(10-7)=23                             

Мы знаем, что единицы вычитаются из единиц, но в числе 30 отдельных единиц нет (строим модель на палочках). Поэтому берем 1 пучок из 3-х, развязываем его и тогда 7 единиц вычитываем из 10 единиц. Получается 23.

30-7= 20+(10-7)=23

6.6ой этап на стр.62 – частный случай вычитания двузначного числа из круглого.

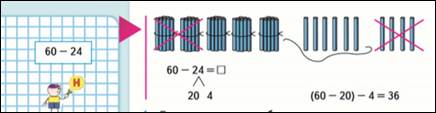
60-24=60-20-4=40-4=36

Сначала разбираем на палочках, опираясь на случай 30-7. Убираем 2 пучка по 10 палочек из 6, затем еще 1 развязываем и убираем 4 палочки из 10:

7.7-ой этап стр.66 - прием сложения двузначных и однозначных чисел с переходом через десяток.   

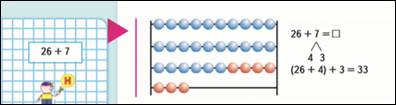
Используют прием прибавления по частям.

26+7=33             Опираемся на прием сложения двух однозначных чисел с

26+(4+3)=33       переходом через разряд.

8.8ой этап на стр. 67 - прием вычитания из двузначного числа однозначного с переходом через разряд.

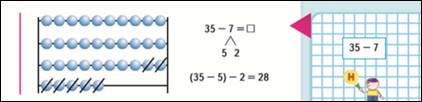
 Используют прием вычитания по частям.

35-7=28      Опираются на прием вычитания в пределах 20

(35-5)-2=28

9.9ый этап в учебнике М2М, 2ч., стр. 4 - прием сложения двузначного числа и двузначного без перехода через разряд.

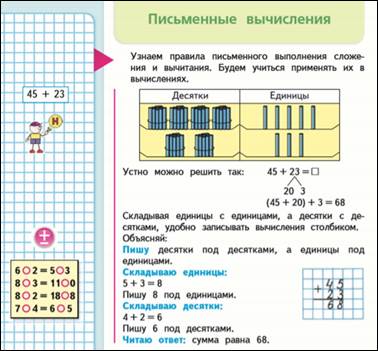
45+23=68

(45+20)+3=68

10.10ый этап в М2М, 2ч., стр. 5 - прием вычитания из двузначного числа двузначного без перехода через разряд.

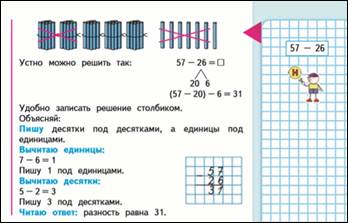
57-26=31

(57-20) -6=31

11.11ый этап. Далее следует рассмотреть прием сложения двузначного числа с двузначным с переходом через десяток, но в учебнике М2М, 2ч такой урок не предусмотрен. Следовательно, учитель включает этот прием в уроки самостоятельно на стр. 11-12.

45+28=73

(45+20)+8=73

12.12ый этап в М2М, 2ч. на стр.29 - прием вычитания из двузначного числа двузначного с переходом через разряд.

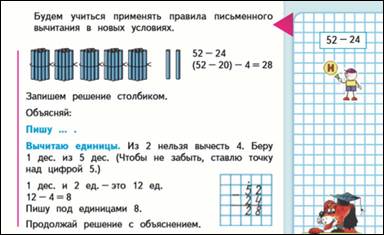
52-24=28

(52-20)-4=28

Таким образом, рассмотрены все случаи сложения и вычитания в пределах 100 и учащиеся должны понять:

1. Принцип поразрядного сложения и вычитания;

2. В процессе устных вычислений сначала прибавляют или вычитают более крупные разрядные единицы, т.е. десятки, а затем более мелкие – единицы. Это отличает устные приемы сложения и вычитания от письменных.

С каждым из названных приемов работают по плану:

1. повторение т.о. данного приема;

2.ознакомления с приемом с помощью наглядных пособий;

3.формирование умения использовать данный прием для вычислений (задания с подробным объяснением и записью);

4.формирование навыка (свернутость, автоматизм, быстрота, обобщенность действий).

Для формирования навыка требуется длительное время. В данной теме результаты не заучиваются, но выполнять действия ребенок должен научиться правильно и быстро. Поэтому в течение длительного времени на каждом уроке предлагаются:

- этапы устного счета (устные упражнения и игры);

- математические диктанты;

- дидактические игры;

- работа с карточками и т.д.

  По другим программам рассматриваются эти же случаи, но (иногда) в другой последовательности и на основе другого методического подхода. Например, по программе Н.Б.Истоминой в основе темы лежит прием моделирования, т.е. по каждому случаю составляют сначала графическую модель (на треугольниках и кругах), а затем - знаковую модель, т.е. равенство. Используют вывод: к единицам прибавляем единицы, к десяткам десятки. По программе Н.Б.Истоминой сначала в 1 классе изучают все случаи без перехода через десяток. Затем во 2 классе вводят все случаи сложения и вычитания в пределах 20 и на их основе все случаи с переходом через десяток в пределах 100.

М1И ч.2 стр. 85                                 М1И ч.2 стр. 87

 

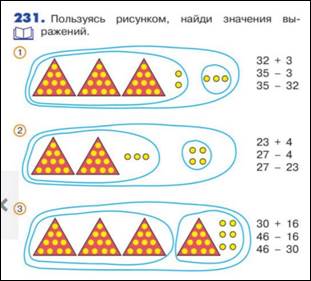
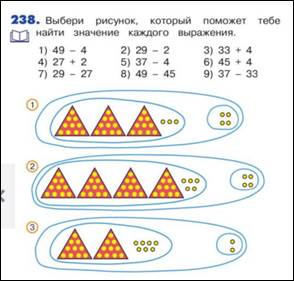
М2И ч.1 стр. 22

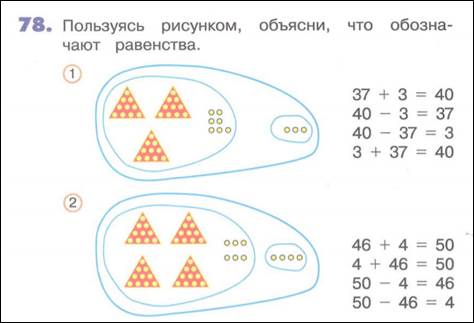
М2М ч.1 стр. 58

Цель урока: познакомить с приёмом вычисления вида 34 +2, 34 +20.

Планируемые результаты обучения

Предметные:

· Ученик будет знать приёмы вычислений вида 34+2,34+20;

· Ученик будет уметь выполнять вычисления вида 34+2,34+20.

Метапредметные:

Познавательные:

-умение строить речевое высказывание в устной форме;

- перерабатывать полученную информацию: наблюдать и делать самостоятельные выводы;

Регулятивные:

-умение принимать и сохранять цели и задачи учебной деятельности, искать и находить средства их достижения;

-умение самостоятельно выделять и формулировать познавательную цель всего урока и отдельного задания;

Коммуникативные:

- умение строить речевое высказывание в устной форме, использовать математическую терминологию;

Личностные:

- самостоятельно определять и высказывать самые простые, общие для всех людей правила поведения при совместной работе и сотрудничестве.
Ресурсы: учебник Математика 2 класс (1часть) [Моро М.И.],

План урока

I. Мотивация (самоопределение) к учебной деятельности (1 – 2 мин.)

II. Актуализация и фиксирование индивидуального затруднения в пробном действии (5 – 6 мин.)

III. Выявление места и причины затруднений (3-5 мин.)

IV. Построение проекта выхода из затруднения (постановка цели) (1-2 мин.)

V. Реализация построенного проекта (7-10 мин).

VI. Первичное закрепление с проговариванием во внешней речи (7 – 10 мин).

VII. Самостоятельная работа с самопроверкой по эталону