Краткие теоретические сведения

Американский исследователь Хопфилд в 80-х годах 20-го века предложил специальный тип нейросетей. Названные в его честь сети Хопфилда являются рекуррентными или сетями с обратными связями и предназначены для распознавания образов. Обобщенная структура этой сети представляется, как правило, в виде системы с обратной связью выхода с входом.

В сети Хопфилда входные сигналы нейронов являются одновременно и выходными сигналами сети: x_i(k)= y_i(k-1), при этом возбуждающий вектор особо не выделяется. В классической системе Хопфилда отсутствует связь нейрона с собственным выходом, что соответствует 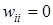, а вся матрица весов является симметричной: w _ij= w_ji        

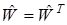.                                                  (1)

Симметричность матрицы весов гарантирует сходимость процесса обучения. Процесс обучения сети формирует зоны притяжения некоторых точек равновесия, соответствующих обучающим данным. При использовании ассоциативной памяти мы имеем дело с обучающим вектором , либо с множеством этих векторов, которые в результате проводимого обучения определяют расположение конкретных точек притяжения (аттракторов).

Каждый нейрон имеет функцию активации сигнум со значениями :

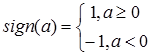.                                                    (2)

Это означает, что выходной сигнал i-го нейрона определяется функцией:

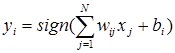,                         (3)

где N обозначает количество нейронов, N= n. Часто постоянная составляющая b_i , определяющая порог срабатывания отдельных нейронов, равна 0. Тогда циклическое прохождение сигнала в сети Хопфилда можно представить соотношением:

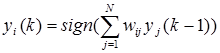                               (4)

с начальным условием .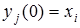

В процессе функционирования сети Хопфилда можно выделить два режима: обучения и классификации. В режиме обучения на основе известных обучающих выборок 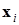 подбираются весовые коэффициенты w_ij. В режиме классификации при зафиксированных значениях весов и вводе конкретного начального состояния нейронов  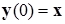возникает переходный процесс, протекающий в соответствии с выражением (2) и заканчивающийся в одном из локальных устойчивых положений, задаваемом биполярным вектором со значениями 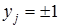, для которого .

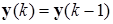Обучение не носит рекуррентного характера. Достаточно ввести значения (правило Хебба) весов, выразив их через проекции вектора точки притяжения эталонного образа:

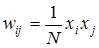,                                                               (5)

В соответствии с этим правилом сеть дает правильный результат при входном примере, совпадающим с эталонным образцом, поскольку:

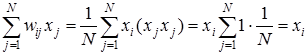,                         (6)

так как вследствие биполярности значений элементов вектора 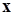 всегда .

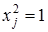При вводе большого количества обучающих выборок 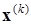 для k=1,2,… p веса w_ij  подбираются согласно обобщенному правилу Хебба в соответствии с которым:

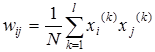.                                                 (7)

Благодаря такому режиму обучения веса принимают значения, определяемые усреднением множества обучаемых выборок. В случае множества обучаемых выборок актуальным становится вопрос о стабильности ассоциативной памяти.

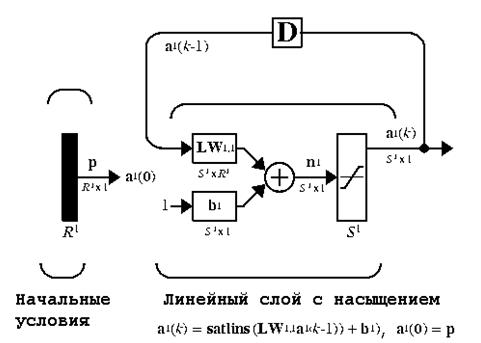
Сеть Хопфилда [2] является автоассоциативной сетью (рис. 12). Дискретная сеть Хопфилда имеет следующие характеристики: она содержит один слой элементов; каждый элемент связывается со всеми другими элементами, но не связан с самим собой; за один шаг работы обновляется только один элемент сети; элементы обновляются в случайном порядке; выход элемента ограничен значениями 0 или 1.

 

Рис. 12. Схема архитектуры модифицированной сети Хопфилда

 

 

Пример решения типовой задачи

Рассмотрим сеть Хопфилда [1] с четырьмя нейронами и определим четыре точки равновесия:

 

T = [+1 -1; -1 +1; +1 +1; -1 -1];

T=T';

plot(T(1,:),T(2,:),'rh','MarkerSize',13), hold on;

axis([-1.1 1.1 -1.1 1.1]);

title('Hopfield Network State Space');

xlabel('a(1)');

ylabel('a(2)');

net = newhop(T);

[Y,Pf,Af] = sim(net,4,[],T);

Y

Pf

Af

Pause

color = 'rgbmy';

for i=1:25

a = {rands(2,1)};

[y,Pf,Af] = sim(net,{1 20},{},a);

record=[cell2mat(a) cell2mat(y)];

start=cell2mat(a);

plot(start(1,1),start(2,1),'kx',record(1,:),

record(2,:), color(rem(i,5)+1),'LineWidth',5)

End

 

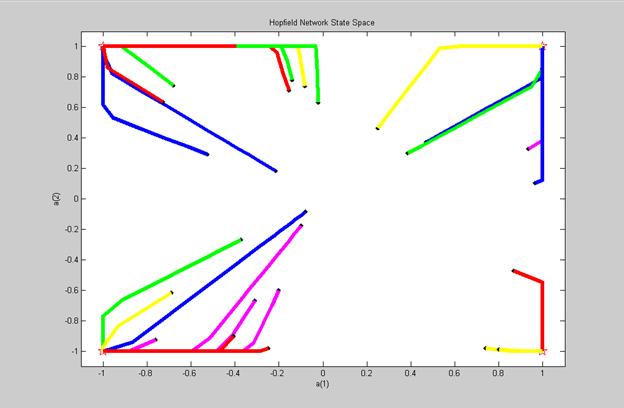
На рис. 13 показано поведение обученной сети при случайных начальных условиях a.

 

Рис. 13. Поведение сети Хопфилда при случайных начальных условиях a

 

 

Отчёт о выполнении работы

Отчёт о выполнении лабораторной работы №4 должен быть выполнен на листах формата А4 и содержать следующие результаты:

1. Исходные данные;

2. Текст программы с подробными комментариями;

3. Результаты моделирования (рис. 13);

4. Контрольный пример;

5. Краткие письменные ответы на контрольные вопросы, содержащиеся в приложении.

 

Контрольные вопросы для лабораторной работы № 8

 

1. Искусственный интеллект. Его истоки и проблемы.

2. Нейрофизиологические данные об обработке информации в биологических системах.

3. Искусственный нейрон. Идея и техническая реализация.

4. Модели нейронов. Типичные виды функций активации нейрона.

5. Многослойный персептрон.

6. Однонаправленные многослойные сети. Алгоритм обратного распространения ошибки.

7. Вывод конкретных формул алгоритма обратного распространения ошибки для двухслойных сетей с малым числом нейронов (2-3).

8. Градиентные методы. Алгоритм наискорейшего спуска. Недостатки метода. Метод моментов.

9. Радиальные нейронные сети. Обучение. Область применения.

10. Рекуррентные сети. Ассоциативная сеть Хопфилда. Обучение. Распознавание образов.

11. Сеть встречного распространения.

12. Обучение слоя Кохонена. Решение задач кластеризации.

13. Статистический подход к обучению нейронной сети. Машина Больцмана и ее модификации.

14. Применение нейронных сетей. Сбор данных для нейронных сетей.

15. Задача регрессии и прогнозирования временных рядов.

16. Основные характеристики пакета MATLAB. Простейшие вычисления. Работа с массивами. Графики функций. Сессия. М-файлы. Mat-файлы.

17. Нейронные сети в пакете MATLAB.