Вероятностная нейронная сеть

(4 часа)

6.1 Цель работы: Получить практические навыки создания и использования вероятностной нейронной сети для решения задачи классификации образцов.

Вероятностная нейронная сеть

При решении задачи классификации можно оценить плотность вероятности для каждого класса, сравнить между собой вероятности принадлежности образца различным классам и выбрать из них самый вероятный.

Вероятностная нейронная сеть является аналогом обобщенно-регрессионной нейронной сети, но она разработана специально для решения задачи классификации образцов. Использование вероятностной НС основано на ядерных оценках плотности вероятности. Можно рассуждать так: тот факт, что наблюдение расположено в данной точке пространства свидетельствует о том, что в этой точке имеется некоторая плотность вероятности. Вблизи наблюдения имеется большее доверие к уровню плотности, а по мере отдаления от него доверие убывает и стремится к нулю. В методе ядерных оценок в точке, соответствующей каждому наблюдению, помещается некоторая простая радиусная функция, затем все они складываются, и в результате получается оценка для общей плотности вероятности. Чаще всего в качестве ядерных функций берутся гауссовы функции (в форме колокола).

Вероятностная нейронная сеть имеет следующую архитектуру: входной слой, слой радиальных базисных элементов (слой образцов) и выходной слой (слой суммирования). Радиальные элементы берутся по одному на каждое обучающее наблюдение. Каждый из них представляет гауссову функцию с центром в этом наблюдении. Каждому классу соответствует один выходной элемент. Каждый такой элемент соединен со всеми радиальными элементами, относящимися к его классу, а со всеми остальными радиальными элементами он имеет нулевое соединение. Таким образом, выходной элемент просто складывает отклики всех элементов, принадлежащих к его классу. Выходной слой работает по принципу "победитель получает всё" (функция compet), т.е. на выход подается единица по классу, имеющему максимальную накопленную сумму, а на выходные элементы, соответствующие другим классам, подаются нули.

Вероятностная нейронная сеть имеет единственный управляющий параметр, значение которого должно выбираться пользователем – степень сглаживания (или отклонение гауссовой функции, spread). Этот параметр выбирается из тех соображений, чтобы "шапки" радиусных функций перекрывались: выбор слишком маленьких отклонений приведет к острым аппроксимирующим функциям и неспособности сети к обобщению, а при слишком больших отклонениях будут теряться детали. Требуемое значение несложно найти опытным путем, подбирая его так, чтобы контрольная ошибка была как можно меньше. Стоит отметить, что вероятностные нейронные сети не очень чувствительны к выбору параметра сглаживания.

Наиболее важные преимущества вероятностных сетей состоят в том, что выходное значение имеет вероятностный смысл (и поэтому его легче интерпретировать), и в том, что сеть быстро обучается. Существенным недостатком таких сетей является их объем. Вероятностная сеть фактически вмещает в себя все обучающие данные, поэтому она может потребовать много памяти и медленно работать. 

Изучаемые функции

Функция создания вероятностной НС

net=newpnn(P, T, spread). P – матрица входных векторов; T – матрица целевых векторов; spread – отклонение (по умолчанию 1,0).

Вспомогательные векторно-матричные функции

ind 2 vec ( ind ) – функция преобразования строки индексов (т.е. целых положительных чисел). Возвращается разреженная матрица с одним единичным элементом в каждом столбце, положение которого определяется исходным набором индексов. Аргумент – строка индексов ind.

Пример:

>> ind=[1 2 4 3]

ind =

1 2 4 3

>> vec=ind2vec(ind)

vec =

(1,1)   1

(2,2)   1

(4,3)   1

(3,4)   1

vec 2 ind ( vec ) – функция, обратная к функции ind 2 vec ( ind ).

Пример :

>> vec=[1 0 0 0;0 0 1 0;0 1 0 0;0 0 0 1]

vec =

1 0 0 0

0 0 1 0

0 1 0 0

0 0 0 1

>> ind=vec2ind(vec)

ind =

1 3 2 4

Пример создания вероятностной нейронной сети.

% Возьмем четыре 2-элементных входных вектора P (координаты четырех точек) и вектор ассоциированных с ними классов Tc:

>> P=[0 1 3 2; 3 1 2.5 4]

P =

0        1.0000 3.0000 2.0000

3.0000 1.0000 2.5000 4.0000

>> Tc=[1 2 3 4];

% Изобразим соответствующие точки на графике (см. рисунок 18)

>> plot(P(1,:),P(2,:),'.','markersize',30)

>> axis([-1 4 0 5])

>> hold on

% Подпишем точки в соответствии с их целевыми классами

>> for i=1:4,text(P(1,i)+0.1,P(2,i), sprintf('klass %g',Tc(i))), end

 

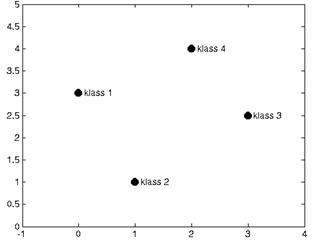
Рисунок 18 – Центры четырех классов

% Конвертируем индексы классов в разреженную матрицу T:

>> T=ind2vec(Tc);

% При создании вероятностной сети примем значение параметра spread =2,

% потому что это примерно равно среднему расстоянию между имеющимися точками.

>> spr=2;

% Создадим вероятностную НС функцией newpnn :

>> net=newpnn(P,T,spr);

% Испытаем созданную НС на входных векторах. Предварительно закроем

% окно с графиком, чтобы нарисовать новый.

>> A=sim(net,P);

% Конвертируем выходную матрицу в индексы классов:

>> Ac=vec2ind(A);

% Построим новый график с надписями классов, определенных сетью (см.

% рисунок 19)

>> plot(P(1,:),P(2,:),'.','markersize',30)

>> axis([-1 4 0 5])

>> hold on

>> for i=1:4,text(P(1,i)+0.1,P(2,i), sprintf('klass %g',Ac(i))), end

 

 

 

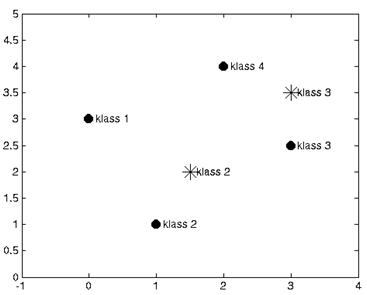
Рисунок 19 – Результаты классификации данных нейронной сетью

% Попробуем классифицировать при помощи созданной НС новые точки:

>> p=[1.5;2];

>> a=sim(net,p);

>> ac=vec2ind(a);

>> plot(p(1),p(2),'r*','markersize',15)

>> text(p(1)+0.1,p(2), sprintf('klass %g',ac))

>> p=[3;3.5];

>> a=sim(net,p);

>> ac=vec2ind(a);

>> plot(p(1),p(2),'r*','markersize',15)

>> text(p(1)+0.1,p(2), sprintf('klass %g',ac))

% Сеть справилась с новыми образцами успешно (см. рисунок 19).

Создайте вероятностную нейронную сеть для классификации образцов по трем заданным классам:

Классы	Вариант 1		Вариант 2		Вариант 3		Вариант 4
	X	Y	X	Y	X	Y	X	Y
Класс 1	0	2	1	2	3	2	1	1
Класс 2	2	4	1	4	1	4	1	3
Класс 3	2	0	3	3	5	4	3	1

Классы	Вариант 5		Вариант 6		Вариант 7
	X	Y	X	Y	X	Y
Класс 1	4	2	2	2	1	1
Класс 2	2,5	4	4	4	3	1
Класс 3	1	2	4	2	3	3

 

Классы	Вариант 8		Вариант 9		Вариант 10
	X	Y	X	Y	X	Y
Класс 1	2	1	4,5	3	1	4
Класс 2	3	3	1	2	6	3
Класс 3	4,5	1,5	3	0	3	1

Контрольные вопросы

1. В чем состоит математическое содержание задачи классификации образцов?

2. Какова архитектура вероятностной нейронной сети? Перечислите ее достоинства и недостатки.

3. Перечислите основные и вспомогательные функции Matlab для работы с вероятностными нейронными сетями.

 

Лабораторная работа № 7

СЛОИ КОХОНЕНА (6 часов)

7.1 Цель работы: Получить практические навыки создания и использования нейронных сетей со слоем Кохонена и самоорганизующихся карт признаков для решения задачи классификации образцов.

7.2 Задача кластеризации и поиска зависимостей

       Кроме задачи классификации, нейросети широко используются для поиска зависимости в данных и кластеризации. Кластеризация – это разбиение набора примеров на несколько компактных областей (кластеров), причем принадлежность образцов конкретным кластерам заранее неизвестна. Кластеризация позволяет представить неоднородные данные в более наглядном виде и использовать далее для исследования каждого кластера различные методы. Например, таким образом можно выявить фальсифицированные страховые случаи, отчетность недобросовестных предприятий, проанализировать случаи производственного травматизма и т.д.

7.3 Слой Кохонена.       Слой Кохонена функционирует по правилу "победитель получает все". Для любого конкретного входного вектора один и только один нейрон Кохонена выдает единицу, все остальные выдают нуль. Активность каждого нейрона Кохонена представляет собой вычисление расстояния между входным сигналом и вектором весов нейрона: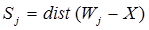

где S_j – активность j-го нейрона Кохонена, W_j=(w_1j,…, w_nj) – вектор весов j-го нейрона Кохонена, X=(x₁,…, x_n) – вектор входного сигнала.

Нейрон Кохонена с минимальным значением S_j является "победителем". Его выход равен единице, у остальных он равен нулю.

7.4 Обучение слоя Кохонена . Слой Кохонена классифицирует входные векторы в группы схожих. Это достигается с помощью такой подстройки весов слоя Кохонена, что близкие входные векторы активизируют один и тот же нейрон данного слоя.

       Слой Кохонена обучается без учителя (самообучается). В результате самообучения слой приобретает способность разделять несхожие входные векторы. Какой именно нейрон будет активизироваться при предъявлении конкретного входного сигнала, заранее предсказать нельзя.

       При обучении слоя Кохонена на его входы последовательно подаются входные вектора. Для каждого образца сначала выявляется нейрон, наиболее близкий к входному сигналу, затем он объявляется "выигравшим", после чего его веса подстраиваются таким образом, чтобы разница между его весами и входным сигналом стала еще меньше.

       Как правило, обучающее множество включает много сходных между собой входных векторов, и сеть должна обучиться активизировать один и тот же нейрон Кохонена для каждого из них. Веса этого нейрона должны получаться усреднением входных векторов, которые должны его активизировать.

7.5 Самоорганизующаяся карта признаков

Самоорганизующаяся карта признаков имеет входные элементы, число которых соответствует размерности входных векторов, и набор выходных элементов (слой Кохонена), которые служат в качестве прототипов кластеров и называются "кластерными элементами". Входные элементы предназначены только для того, чтобы распределять данные входного вектора между нейронами слоя Кохонена. Часто удобно интерпретировать веса кластерных элементов как значения координат, описывающих положение кластера в пространстве входных данных.

Карта признаков проходит два этапа обучения. На первом этапе элементы упорядочиваются так, чтобы отражать пространство входных элементов, а на втором этапе происходит уточнение их позиций. В начале обучения карта выглядит сильно "измятой", в ходе обучения она постепенно разворачивается и расправляется.

Обычно число кластерных элементов выбирают значительно меньшим, чем число учебных образцов, поскольку целью работы является получение упрощенной модели множества данных. К концу обучения кластерные элементы обеспечивают "информационную сводку" по пространству входных образцов.