net=newc(PR, S, KLR, CLR) – функция создания слоя Кохонена. Функция использует аргументы: PR – Rх2 матрица минимальных и максимальных значений для R входных элементов, S – число нейронов, KLR – коэффициент обучения Кохонена (по умолчанию 0,01), CLR – коэффициент "справедливости" (по умолчанию 0,001).
net=newsom(PR, [D1, D2,…], TFCN, DFCN, OLR, OSTEPS, TLR, TND) – функция создания самоорганизующейся карты с аргументами: PR – Rх2 матрица минимальных и максимальных значений для R входных элементов, Di – размеры i-го слоя, по умолчанию [5 8], TFCN – топологическая функция, по умолчанию 'hextop', DFCN – функция расстояния, по умолчанию 'linkdist',
 OLR – коэффициент обучения фазы упорядочивания, по умолчанию 0,9, OSTEPS – число шагов фазы упорядочивания, по умолчанию 1000, TLR – коэффициент упорядочивания фазы настройки, по умолчанию 0,02, TND – расстояние для фазы настройки (по умолчанию 1).
OLR – коэффициент обучения фазы упорядочивания, по умолчанию 0,9, OSTEPS – число шагов фазы упорядочивания, по умолчанию 1000, TLR – коэффициент упорядочивания фазы настройки, по умолчанию 0,02, TND – расстояние для фазы настройки (по умолчанию 1).
Вспомогательные функции
hextop( dim1, dim2,…, dimN) – функция размещения нейронов в узлах гексагональной (шестиугольной) решетки. Возвращает матрицу, содержащую N строк и (dim1 х dim2 х…х dimN) столбцов с координатами нейронов
plotsom( pos) – функция возвращает графическое представление расположения нейронов в самоорганизующихся картах.
Пример: pos = hextop(3,4)
pos =
0 1.0000 2.0000 0.5000 1.5000 2.5000 0 1.0000 2.0000 0.5000 1.5000 2.5000
0 0 0 0.8660 0.8660 0.8660 1.7321 1.7321 1.7321 2.5981 2.5981 2.5981
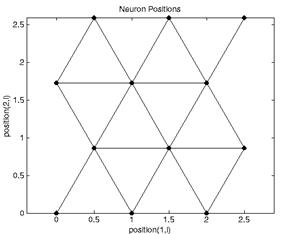
>> plotsom(pos) % Результат см. на рисунке 20
Рисунок 20 – Результат выполнения функции plotsom
Порядок выполнения работы
1. Кластеризация данных. Исходные данные приведены в таблице 3.
Таблица 3 – Исходные данные для кластеризации
| x
| 0.09
| 0.1
| 0.15
| 0.3
| 0.35
| 0.32
| 0.25
| 0.7
| 0.7
| 0.8
| 0.75
| 0.79
|
| y
| 0.48
| 0.41
| 0.55
| 0.3
| 0.4
| 0.35
| 0.50
| 0.7
| 0.75
| 0.65
| 0.9
| 1
|
% Нанесем данные на график, установим размеры осей:
>> plot(P(1,:),P(2,:),'+r');
>> axis([0 1 0 1.5]);
>> hold on;
% На графике видны три кластера. Создадим слой Кохонена, состоящий из 3-х нейронов:
>> net=newc([0 1;0 1],3,0.1);
% Установим количество эпох обучения:
>> net.trainParam.epochs=10;
% запишем в массив w веса слоя Кохонена
>> w=net.IW{1};
% Нанесем их на график. Сеть еще не обучена, поэтому все веса изображены в виде одной точки посредине исследуемой области
>> h=plot(w(:,1),w(:,2),'ob');
% Запустим обучение сети. Сеть обучается самостоятельно (без учителя). Задание целевых векторов не требуется
>> net=train(net,P);
TRAINR, Epoch 0/10
TRAINR, Epoch 10/10
TRAINR, Maximum epoch reached.
% Запишем веса в массив w:
>> w=net.IW{1};
% Удалим точку, изображавшую веса необученного слоя Кохонена:
>> delete(h);
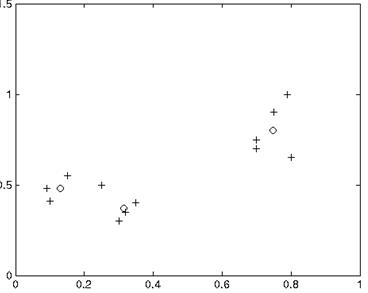
% Нанесем на график веса обученных нейронов (см. рисунок 21). Теперь веса нейронов слоя Кохонена соответствуют центрам кластеров опытных данных
>> h=plot(w(:,1),w(:,2),'ob');
% Подпишем классы в соответствии с решением сети:
>> W=w';
>> for i=1:3, text(w(i,1)+0.01,w(i,2), sprintf('k %g',vec2ind(sim(net,W(:,i))))),end
 % Проверим способность сети к классификации на данных, как входящих в обучающую выборку, так и новых:
% Проверим способность сети к классификации на данных, как входящих в обучающую выборку, так и новых:
>> p=[0.25;0.5];
>> a=sim(net,p)
a =
(3,1) 1
>> plot(p(1),p(2),'k*');
>> p=[0.2;0.5];
a=sim(net,p)
a = (2,1) 1
>> plot(p(1),p(2),'k*');
Рисунок 21 – Выявленные сетью центры кластеров (о)
>> p=[0.4;0.5];
a=sim(net,p)
a =
(3,1) 1
>> plot(p(1),p(2),'k*');
>> p=[0.8;0.75];
a=sim(net,p)
a = (1,1) 1
>> plot(p(1),p(2),'k*');
% По желанию можно преобразовывать разреженную матрицу решения сети в натуральный индекс при помощи функции vec2ind.
Пример создания самоорганизующейся карты.
% Сгенерируем тестовые данные - 1000 случайных точек в диапазоне координат (-1,1) и нанесем их на график:
>> P=rands(2,1000);
>> plot(P(1,:),P(2,:),'+r')
% Создадим самоорганизующуюся карту размером 5 х 6 нейронов:
 >> net=newsom([0 1;0 1],[5 6]);
>> net=newsom([0 1;0 1],[5 6]);
% Нанесем веса нейронов на график. Карта еще не обучилась, поэтому все веса изображены в виде единственной точки
>> plotsom(net.iw{1,1},net.layers{1}.distances)
% Установим количество эпох обучения = 1. Так как данных много, достаточно 1 эпохи обучения. В более сложных ситуациях количество эпох для полной организации карты может составлять 100-200
>> net.trainParam.epochs=1;
% Запустим механизм самообучения
>> net=train(net,P);
TRAINR, Epoch 1/1; TRAINR, Maximum epoch reached.
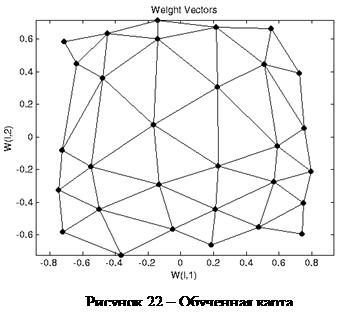
% Изобразим полученную в результате обучения карту на графике (см. рисунок 22)
>> plotsom(net.iw{1,1},net.layers{1}.distances)
% Теперь если мы сформируем произвольный вектор входа, то самоорганизующаяся карта Кохонена должна указать его принадлежность тому или иному кластеру (классу):
>> p=[0.5;0.3];
>> a=sim(net,p)
a = (16,1) 1
Указанный вектор принадлежит шестнадцатому кластеру.
1 Создайте слой Кохонена для кластеризации входных данных:
|
Вариант
|
Вариант
|
Вариант
|
Вариант
|
Вариант
|
| x
| y
| x
| y
| x
| y
| x
| y
| x
| y
|
| 1
| 1
| 7,5
| 1
| 1,5
| 1
| 1,5
| 1
| 1,5
| 1
|
| 2
| 2
| 8
| 2
| 2,5
| 2
| 2,5
| 2
| 2,5
| 2
|
| 3
| 1
| 8,5
| 1
| 2,5
| 1
| 2
| 3
| 2
| 3
|
| 1,5
| 10
| 4,5
| 4,5
| 5,5
| 4,5
| 5,5
| 4,5
| 7
| 1,5
|
| 5
| 5
| 3,5
| 5
| 4,5
| 4,5
| 4,5
| 4,5
| 6,5
| 2
|
| 6
| 4,5
| 5
| 5,5
| 5
| 5,5
| 5
| 5,5
| 6
| 1,5
|
| 5,5
| 6
| 3,5
| 6
| 6
| 6
| 6
| 6
| 6
| 9
|
| 8
| 10
| 8
| 10
| 8,5
| 10
| 2
| 10
| 2
| 10
|
| 9
| 9
| 9
| 9
| 1,5
| 9
| 5
| 6,5
| 5,5
| 8,5
|
| 1
| 10
| 7,5
| 9
| 7,5
| 9
| 1,5
| 9
| 5,5
| 9,5
|
| 2
| 11
| 8,5
| 8
| 1
| 8
| 1
| 8
| 1
| 8
|
| 3
| 10
| 7,5
| 10
| 7,5
| 10
| 1
| 10
| 1
| 10
|
|
Вариант
|
Вариант
|
Вариант
|
Вариант
|
Вариант
|
| x
| y
| x
| y
| x
| y
| x
| y
| x
| y
|
| 1,5
| 3
| 1,5
| 1
| 1,5
| 7,5
| 2
| 6
| 1,5
| 1,5
|
| 1
| 4,5
| 2,5
| 2
| 2,5
| 1,5
| 2
| 7
| 1
| 6,5
|
| 2
| 5
| 2,5
| 1
| 6,5
| 4
| 5,5
| 5
| 4
| 2,5
|
| 7
| 1,5
| 5,5
| 4,5
| 2
| 6
| 8
| 1
| 8
| 4
|
| 6,5
| 2
| 4,5
| 4,5
| 3
| 7,5
| 3
| 8
| 3,5
| 1,5
|
| 4,5
| 8
| 5
| 5,5
| 2
| 9
| 1
| 1
| 1,5
| 7
|
| 6
| 9
| 6
| 6
| 9
| 2,5
| 5
| 3,5
| 7
| 3,5
|
| 5
| 10,5
| 8,5
| 10
| 8
| 3
| 8
| 2
| 7,5
| 5
|
| 5,5
| 8,5
| 1,5
| 9
| 2,5
| 3
| 4,5
| 4,5
| 2,5
| 2
|
| 5,5
| 9,5
| 7,5
| 9
| 9
| 4
| 1,5
| 2
| 2
| 6
|
| 1
| 6
| 1
| 8
| 3
| 2,5
| 2
| 1
| 8,5
| 5
|
| 4,5
| 9,5
| 7,5
| 10
| 7,5
| 5
| 9
| 2,5
| 2,5
| 1
|
2 Создайте самообучающуюся карту признаков для кластеризации данных. Тестовые данные сгенерируйте случайным образом в квадрате (-1,1)´(-1,1) в количестве:
| 1 вариант
| 2 вариант
| 3 вариант
| 4 вариант
| 5 вариант
|
| 50
| 100
| 150
| 200
| 250
|
| 6 вариант
| 7 вариант
| 8 вариант
| 9 вариант
| 10 вариант
|
| 300
| 350
| 400
| 450
| 500
|
Контрольные вопросы
1. В чем суть задачи кластеризации образцов?
2. Что из себя представляет слой Кохонена, самоорганизующаяся карта признаков? Как они обучаются?
3. Приведите функции Matlab для работы со слоем Кохонена, самоорганизующейся картой признаков.
Лабораторная работа № 8
Сеть Хопфилда
Цель работы
Научиться работать с сетью Хопфилда newhop, исследовать устойчивость сети и её сходимость.





 OLR – коэффициент обучения фазы упорядочивания, по умолчанию 0,9, OSTEPS – число шагов фазы упорядочивания, по умолчанию 1000, TLR – коэффициент упорядочивания фазы настройки, по умолчанию 0,02, TND – расстояние для фазы настройки (по умолчанию 1).
OLR – коэффициент обучения фазы упорядочивания, по умолчанию 0,9, OSTEPS – число шагов фазы упорядочивания, по умолчанию 1000, TLR – коэффициент упорядочивания фазы настройки, по умолчанию 0,02, TND – расстояние для фазы настройки (по умолчанию 1). % Проверим способность сети к классификации на данных, как входящих в обучающую выборку, так и новых:
% Проверим способность сети к классификации на данных, как входящих в обучающую выборку, так и новых: >> net=newsom([0 1;0 1],[5 6]);
>> net=newsom([0 1;0 1],[5 6]);


