Как было показано Вином при увеличении напряженности поля до значений 10-4 – 10-5 В/см величина электропроводности возрастает непропорционально закону Ома. Согласно теории Дебая-Хюккеля, ионная атмосфера характеризуется определенным размером и временем релаксации.
При достаточно высокой напряженности поля путь, пройденный ионом за удвоенное время релаксации ионной атмосферы, может оказаться больше, чем радиус ионной атмосферы, и ионная атмосфера не будет успевать образовываться, а обусловленные ею эффекты торможения исчезнут.
Влияние частоты электрического поля
На эквивалентную электропроводность
При невысокой частоте электрического поля ион при своем движении колеблется с частотой поля. Однако при увеличении частоты эта связь нарушается. Ион при перемещении остается в симметричном положении по отношению к ионной атмосфере и релаксационный эффект торможения исчезает, но электрофоретический эффект сохраняется. Поэтому эквивалентная электропроводность, хотя и возрастает, но не достигает предельной величины. Частота переменного тока, при которой проявляется эффект, обратно времени релаксации. Этот эффект называется дисперсией электропроводности или эффект Дебая-Фалькенхагена.
Закон Кольрауша
В разбавленных растворах сильных электролитов выполняется эмпирический закон Кольрауша (закон квадратного корня):
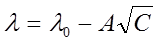 , (6)
, (6)
где λ и λ0 – эквивалентная электропроводность раствора при концентрации С и при бесконечном разведении; А – константа (при данной температуре) для данного электролита и растворителя, полученная с учетом сил релаксационного и электрофоретического торможения. При построении графика зависимости λ от 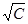 из отсекаемого участка можно установить значение
из отсекаемого участка можно установить значение 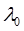 (рис. 3).
(рис. 3).
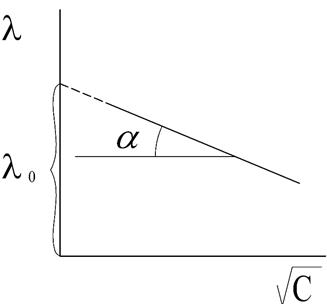
Рис. 3. Зависимость 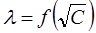 для сильного электролита
для сильного электролита
Однако для более концентрированных растворов многих одновалентных солей (например, NaCl, KCl с концентрацией С=0,001-0,1 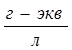 ) и для растворов слабых электролитов уравнение Кольрауша не применимо. Для них справедливо уравнение Гхоша (закон корня кубичного):
) и для растворов слабых электролитов уравнение Кольрауша не применимо. Для них справедливо уравнение Гхоша (закон корня кубичного):
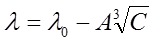 . (7)
. (7)
Согласно закону Кольрауша о независимой миграции ионов, эквивалентная электропроводность раствора при бесконечном разведении равна сумме предельных подвижностей катионов и анионов (закон аддитивности элктропроводности):
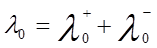 , (8)
, (8)
где 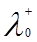 и
и 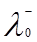 – ионные электропроводности при бесконечном разведении или подвижности катиона и аниона. Физический смысл этого закона заключается в том, что в растворе электролита ионы переносят электрический ток независимо друг от друга.
– ионные электропроводности при бесконечном разведении или подвижности катиона и аниона. Физический смысл этого закона заключается в том, что в растворе электролита ионы переносят электрический ток независимо друг от друга.
Закон формулируется в виде:
эквивалентная электропроводность электролита при бесконечно разведении равна сумме эквивалентных электропроводностей ионов, образующих молекулу электролита.
Закон применим как для сильных, так и для слабых электролитов.
В растворах слабых электролитов 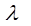 и
и 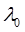 связаны со степенью диссоциации α электролита уравнением Аррениуса:
связаны со степенью диссоциации α электролита уравнением Аррениуса:
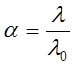 . (9)
. (9)
Закон разведения Оствальда
Для слабых электролитов, выполняется закон разведения Оствальда, который для бинарного электролита записывается следующим образом:
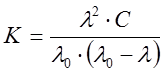 . (10)
. (10)
Приводя данное уравнение к линейной форме, получим
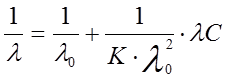 , (11)
, (11)
где 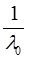 и
и 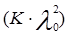 – величины постоянные. Если построить график в координатах
– величины постоянные. Если построить график в координатах 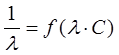 , то получаемая зависимость будет линейной с угловым коэффициентом
, то получаемая зависимость будет линейной с угловым коэффициентом 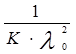 (рис. 4). Такая обработка экспериментальных данных позволяет графически определить величины константы диссоциации и эквивалентную электропроводность.
(рис. 4). Такая обработка экспериментальных данных позволяет графически определить величины константы диссоциации и эквивалентную электропроводность. 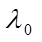
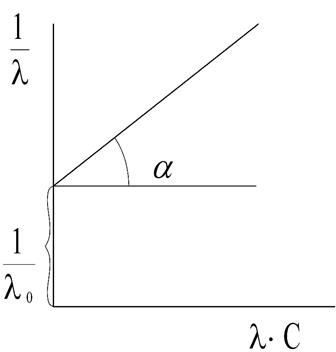
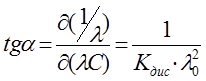
Рис. 4. Зависимость 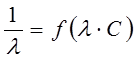 для слабого электролита
для слабого электролита
Для электролита 1,1-валентного типа закон разведения Оствальда можно записать в виде:
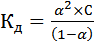 (12)
(12)
Если α<<1, то уравнение примет вид:
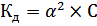 (13)
(13)
Формула (13) позволяет рассчитать степень диссоциации слабого бинарного электролита при различных концентрациях для разбавленных растворах. Степень диссоциации зависит от природы растворителя и самого слабого электролита, от температуры, от присутствия посторонних электролитов, и возрастает с уменьшением концентрации раствора данного слабого электролита.
Константа диссоциации – константа равновесия процесса диссоциации слабого электролита, поэтому по зависимости константы диссоциации от температуры для растворов слабых электролитов рассчитывают ряд термодинамических функций.
Максимально полезная работа процесса диссоциации, протекающего обратимо и изотремически, может быть рассчитана по уравнению изотермы
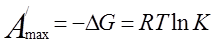 . (14)
. (14)
Если известна константа диссоциации при нескольких температурах, то по уравнению изобары можно рассчитать тепловой эффект процесса диссоциации:
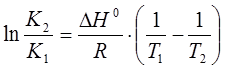 , (15)
, (15)
где К1 и К2 – константы диссоциации при разных температурах; 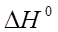 – тепловой эффект процесса диссоциации.
– тепловой эффект процесса диссоциации.
При определенных изобарно-изотермическом потенциале 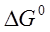 и тепловом эффекте процесса диссоциации
и тепловом эффекте процесса диссоциации 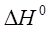 можно найти изменение энтропии
можно найти изменение энтропии 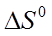 по уравнению
по уравнению
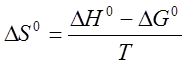 . (16)
. (16)





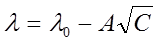 , (6)
, (6)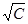 из отсекаемого участка можно установить значение
из отсекаемого участка можно установить значение 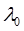 (рис. 3).
(рис. 3).
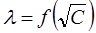 для сильного электролита
для сильного электролита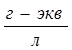 ) и для растворов слабых электролитов уравнение Кольрауша не применимо. Для них справедливо уравнение Гхоша (закон корня кубичного):
) и для растворов слабых электролитов уравнение Кольрауша не применимо. Для них справедливо уравнение Гхоша (закон корня кубичного):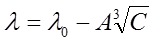 . (7)
. (7)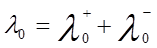 , (8)
, (8)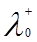 и
и 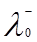 – ионные электропроводности при бесконечном разведении или подвижности катиона и аниона. Физический смысл этого закона заключается в том, что в растворе электролита ионы переносят электрический ток независимо друг от друга.
– ионные электропроводности при бесконечном разведении или подвижности катиона и аниона. Физический смысл этого закона заключается в том, что в растворе электролита ионы переносят электрический ток независимо друг от друга.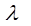 и
и 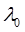 связаны со степенью диссоциации α электролита уравнением Аррениуса:
связаны со степенью диссоциации α электролита уравнением Аррениуса: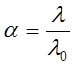 . (9)
. (9)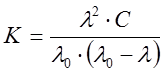 . (10)
. (10)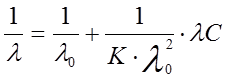 , (11)
, (11)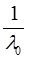 и
и 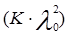 – величины постоянные. Если построить график в координатах
– величины постоянные. Если построить график в координатах 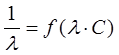 , то получаемая зависимость будет линейной с угловым коэффициентом
, то получаемая зависимость будет линейной с угловым коэффициентом 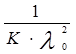 (рис. 4). Такая обработка экспериментальных данных позволяет графически определить величины константы диссоциации и эквивалентную электропроводность.
(рис. 4). Такая обработка экспериментальных данных позволяет графически определить величины константы диссоциации и эквивалентную электропроводность. 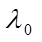

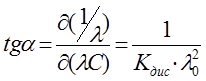
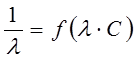 для слабого электролита
для слабого электролита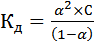 (12)
(12)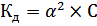 (13)
(13)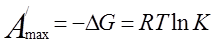 . (14)
. (14)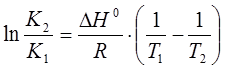 , (15)
, (15)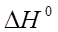 – тепловой эффект процесса диссоциации.
– тепловой эффект процесса диссоциации.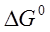 и тепловом эффекте процесса диссоциации
и тепловом эффекте процесса диссоциации 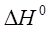 можно найти изменение энтропии
можно найти изменение энтропии 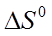 по уравнению
по уравнению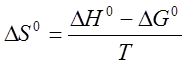 . (16)
. (16)

