

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Будем решать задачу по к критериям:
max f1 = 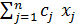
max f2 = 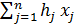
min fk =  , k=3,k
, k=3,k
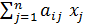 ( ≤ , = , ≥ ) bi , i=1,m
( ≤ , = , ≥ ) bi , i=1,m
xj ≥ 0, j=1,n
Запишем условия равенства относит.отклонений критериев от их экстримальн.значений.
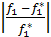 =
=  =…=
=…= 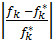
Рассмотрим 4 первых критерия. По условию задачи f1 и f2 максимизир-ся, а f3, f4-минимизир-ся. Проанализируем знач-я 2-х первых критериев.Если
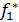 <0 и f*2<0 , то
<0 и f*2<0 , то 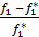 >0 и
>0 и 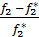 >0 Если f1*>0 и f2*>0 , то
>0 Если f1*>0 и f2*>0 , то 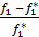 <0 и
<0 и 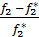 <0.
<0.
Поэтому в равенстве относит.отклонений этих критериев модуль абсолютных величин можно опустить. Тогда получим:
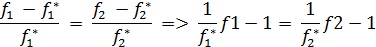
Введем обозначения: 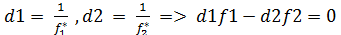
Для критериев f3, f4 получим точно такое же уравнение, т.к. направления их оптимизации совпадают.
Рассмотрим критерии с противоположными направлениями оптимизации f1и f3.Если f1*<0,
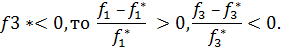
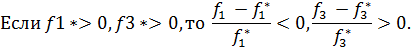
Поэтому при опускании знака модуль перед одним из выражений надо поставить «-». Получим: 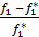 = -
= -  => d1f1+d3f3=2
=> d1f1+d3f3=2
Т.о., для нахождения компромиссного решения методом равных и наим. относ. отклонений необх. оптимизир-е критерии включить в число неизвестных задачи и к основным ограничениям добавить след. ограничения: d1f1-d2f2=0 – для всех fk, кот. как и f1 максимизир-ся; d1f1+d3f3=2 - для всех fk, кот. минимизир-ся. В качестве ЦФ можно взять любую
37. Метод минимакса
Согласно данного м-да сначала решается исходная задача по каждому критерию в отдельности и находятся знач-я f1*,f2*,…,fk*.
Предположим, что компромиссное решение найдено и  , j=1,n - знач-я компонент этого решения. Используя найденные знач-я fk*, k=1,k запишем отностит. отклонения от значений функций в компромиссном решении:
, j=1,n - знач-я компонент этого решения. Используя найденные знач-я fk*, k=1,k запишем отностит. отклонения от значений функций в компромиссном решении:
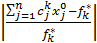 = yk, k=1,k (1)
= yk, k=1,k (1)
Среди знач-ий yk найдем наибольшее и потребуем,чтобы в исходном компромиссном решении оно было минимальным. Тогда ЦФ запишется: min F= max yk Последняя запись и указывает на название м-да.
|
|
Подставим в (1) наибольшее отклонение, предварит-но обозначив его через xn+1= max yk:
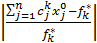 ≤ xn+1, k=1,k (2)
≤ xn+1, k=1,k (2)
Т.к. в практич. задачах  >0 , то умножим ф-лу (2) на знаменатель:
>0 , то умножим ф-лу (2) на знаменатель:
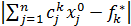 ≤
≤  xn+1, k=1,k (3) Учитывая то. чот знач-я максимизир-х критериев будут >, чем знач-я критериев при компромиссном решении, а величины минимизир-х критериев >, то получим для максимизир-х критериев:
xn+1, k=1,k (3) Учитывая то. чот знач-я максимизир-х критериев будут >, чем знач-я критериев при компромиссном решении, а величины минимизир-х критериев >, то получим для максимизир-х критериев:
 <0 =>
<0 =>  = - (
= - (  )
)
Тогда ф-ла (3) запишется: 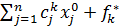 xn+1 ≥
xn+1 ≥  (4)
(4)
Если провести аналогичные рассждения для максимизир-х критериев, то получим:  xn+1 ≤
xn+1 ≤  (5)
(5)
Но т.к. знач-я  и xn+1 не определены, то будем считать их неизвестными в задаче. Тогда доп. ограничения будут иметь вид (4) и (5), в кот.
и xn+1 не определены, то будем считать их неизвестными в задаче. Тогда доп. ограничения будут иметь вид (4) и (5), в кот.  будет заменено на xj. В кач-ве ЦФ берется ф-ция min F= xn+1.
будет заменено на xj. В кач-ве ЦФ берется ф-ция min F= xn+1.
38. Предмет и основные понятия теории игр
Во многих областях человеч. деятельности встречаются проблемы принятия управленческих решений в условиях неопределенности. При этом неопред-ть м.б. связана как с сознат. действиями конкурента, так и др. факторами, влияющими на эффект-ть принимаемого решения. Ситуации, в кот. эффект-ть принимаемого решения зависит от действий др. стороны, наз-ся конфликтными.
Теория игр- раздел математики, изучающий конфликтные ситуации на основе математич. моделей, т.е. это математ. теория, разрабатывающая оптимальн. правила поведения каждого из участников конфликтной ситуации.
Конфликт. ситуация наз-ся антогонистической, если увелич-е выигрыша одной из сторон на некот. величину приведет к уменьш-ю выигрыша др. стороны на такую же величину и наоборот.
Стороны, участвующие в игре наз-ся игроками.
Стратегия игрока- совок-ть правил, однозначно определяющих последоват-ть действий игрока в конкрет. ситуации. Стратегия игрока наз-ся оптимальной, если она обеспечивает данному игроку при многократном повторении игры max возможный средний выигрыш или min возможный средний проигрыш независимо от поведения конкурента.
Партией наз-ся каждый вариант реализ-и игры определ. образом. Выбор одной из стратегий и ее реализ-я наз-ся ходом. Ход наз-ся личным, если игрок сознательно выбирает стратегию. Ход наз-ся случайным, если выбор осущ-ся случайным механизмом.В завис-ти от кол-ва участников игры м.б. парными и множественными. В завис-ти от кол-ва стратегий: конечные, бесконечные.В конце партии каждый игрок Ai, i=1,m получает некоторую сумму ai, кот. наз-ся функцией выигрыша (платежная ф-ция). Она может выражаться как количественно, так и выражением.
|
|
Если ai>0, то это говорит о выигрыше i-го игрока. Если ai<0 –о проигрыше. Если ai=0 –ничейный исход.В завис-ти от вида ф-ции выигрыша игры подразделяются на матричные, биматричные, непрерывные, выпуклые и т.д.
39.Матр. игры с нулев. сумм. Будем рассм. парные игры, т.е. игры, в котор. из 2-х игр. А и В конеч. число стратег. В больш-ве случ. мы имеем игры с нулев. сумм., т.е. игры, в кот-ых выигр. одного игр. = проигр. другого. Парную конеч. игру удобно исслед., если она предст. в виде платеж. матрицы:
| В1 | В2 | … | Вn | |
| А1 | а11 | а12 | … | a1n |
| А2 | а21 | а22 | … | a2n |
| … | … | … | … | … |
| Аm | am1 | am2 | … | Amn |
Здесь кажд. число а(ij), i=1,m , j=1,n явл-ся действит. числом и предст. собой сумму выигр., уплачив. игроком В игроку А, если игр. А выбир. стратегию, соотв-ую i-ой строке, а игр. В выбир. стратегию, соотв-ую j-ому столб. Такую игру назыв. матр-ой игрой mхn.
Целью участн. любой матр. игры явл. выбор наиб. выгодных стратег., к-ые доставл. игр. А макс. выигр., а игр. В миним. проигр.
Чистая стратег. Аi, i=1,m игр. А (чист. стратег. Bj, j=1,n игр. В) назыв. возм-ый ход игр. А(игр. В), выбран. им с вероятн. 1.
Если игра сост. из личных ходов, то выбор пары чистых стратег. (Аi, Вj) единств. образом опред-т исход игры.
Если же в игре испол-ся случ. ходы, то исход игры опред-тся мат. ожид.
Стратег. игр.А назыв. оптимальной, если при её примен-и выигр. игр.А не уменьш., какими бы стратег. не польз-ся игр.В.
Оптим-ой для игр.В назыв. стратег., при кот-ой проигр. игр.В не увелич-ся, какие бы стратег. не примен. игр.А.
40.Реш-е матр-х игр чистых стратег. Если игр.А имеет m стратег., а игр.В имеет n стратег., то для любой пары стратег. их чистые стратег. можно предст-ть в виде единич-х векторов. Напр., для пары стратег. (Аi,Вj) единич-ые вектора будут иметь вид:
pi=(0,…,0,1,0,…0), 1 – i-ое место; qj=(0,…,0,1,0…,0), 1-j-ое место.
При нахожд. оптим-ых стратег. игроки опираются на принцип осторож-ти, при к-ом игроки счит-ся одинаково разумными. Использ-я этот принцип найдем оптим. стратег. игр.АиВ.
|
|
Игр.А для каждой стратег. Аi, i=1,m сначала найдем миним. значен. ожидаемого выигр.
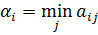
i=1,m, затем, среди знач-ий αi-ых выберем максим.
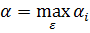
Вел-на α назыв. нижней чистой ценой игры(максимино):

α – гарантир-ый выигр., к-ый может обесп-ть себе игр.А при любом поведение игр.В.
Стратег.  , j, обеспеч- ая получ-е нижней цены игры, назыв. макисм-ой стратег. Игр.В для каждой стратег.Вj, j=1,m выберет маским. знач-е:
, j, обеспеч- ая получ-е нижней цены игры, назыв. макисм-ой стратег. Игр.В для каждой стратег.Вj, j=1,m выберет маским. знач-е:
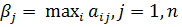 Затем, из βj выберет миним. знач-е:
Затем, из βj выберет миним. знач-е:

Аналог-но, стратег. 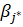 , обеспеч-ая верхнюю чистую цену игры β назыв-ся миним. стратег.
, обеспеч-ая верхнюю чистую цену игры β назыв-ся миним. стратег.
Теорема: В матрич. игре нижняя цена игры не превосх-т верхней чистой цены игры:α≤β. Док-во: по опред-ию

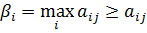
Объед-м последние два соотн-я . Получим:
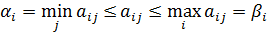
Отсюда 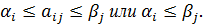 Данное нерав-во справедливо при любых комбинац. i и j. Оно будет справедливо и для тех i и j, для к-ых
Данное нерав-во справедливо при любых комбинац. i и j. Оно будет справедливо и для тех i и j, для к-ых
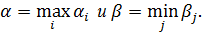
Значит, для этих i и j справед-во α≤β.
41.Игры с седловой точкой. Если в матр. игре нижн. и верх. чистые цены совпад-т, т.е. α=β, то такие игры назыв. играми с седловой точкой.
Знач-е ᴠ=α=β назыв. чистой ценой игры, а стратег. 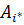 и
и  назыв. оптим. чистыми стратег-ми.
назыв. оптим. чистыми стратег-ми.
Пара чистых стратег. 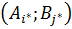 назыв. седловой точкой матрич. игры.
назыв. седловой точкой матрич. игры.
Элемент  назыв. седловым элем. платеж. матр.
назыв. седловым элем. платеж. матр.
Признаком матр. игры с седловой точкой явл-ся выраж-е
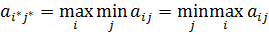
Элем.  явл-ся наименш. в строке
явл-ся наименш. в строке 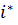 и наибольш. в столбце с номером
и наибольш. в столбце с номером 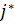 . Реш-ем явл-ся тройка чисел (
. Реш-ем явл-ся тройка чисел ( 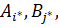
 ).
).
|
|
|

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!