

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
Топ:
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
1) Сначала нужно найти общее решение соответствующего однородного уравнения. Взять уравнение 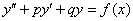 , откинуть правую часть:
, откинуть правую часть: 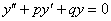 – и найти общее решение.
– и найти общее решение.
2) Необходимо найти какое-либо частное решение  неоднородного уравнения. Сделать это можно так называемым способом подбора частного решения с применением метода неопределенных коэффициентов.
неоднородного уравнения. Сделать это можно так называемым способом подбора частного решения с применением метода неопределенных коэффициентов.
3) На третьем этапе надо составить общее решение 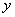 неоднородного уравнения.
неоднородного уравнения. 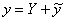 .
.
Пример
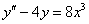
Решение:
1)Сначала найдем общее решение соответствующего однородного уравнения. Берём наш неоднородный диффур 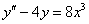 и обнуляем правую часть:
и обнуляем правую часть:

Составим и решим характеристическое уравнение:
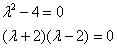
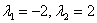 – получены различные действительные корни, поэтому общее решение:
– получены различные действительные корни, поэтому общее решение:
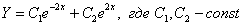
2) Теперь нужно найти какое-либо частное решение  неоднородного уравнения
неоднородного уравнения
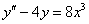
Частное решение тоже следует искать в виде многочлена третьей степени:
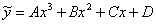 ,
,
где  – пока ещё неизвестные коэффициенты (числа).
– пока ещё неизвестные коэффициенты (числа).
Найдём первую и вторую производную:
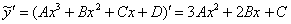
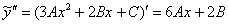
Подставим  и
и 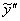 в левую часть неоднородного уравнения:
в левую часть неоднородного уравнения:
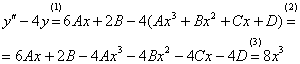
Далее работаем с последним равенством – необходимо приравнять коэффициенты при соответствующих степенях и составить систему линейных уравнений. В картинках процесс выглядит так:
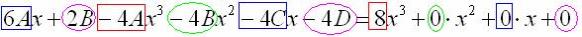
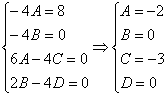
Подставляем найденные значения  в наш исходный подбор частного решения
в наш исходный подбор частного решения
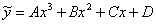 :
:
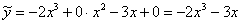
Таким образом, подобранное частное решение неоднородного уравнения:
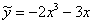
3) Запишем общее решение неоднородного уравнения:
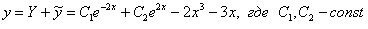
Ответ: общее решение:
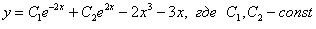
Проверим метод неопр. Коэффициентов, верно ли найдена вторая часть ответа (подобранное частное решение): 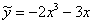 . Найдем первую и вторую производную:
. Найдем первую и вторую производную:
|
|
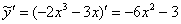
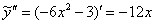
Подставим 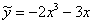 и
и  в левую часть неоднородного уравнения:
в левую часть неоднородного уравнения:
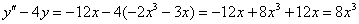
– получена правая часть исходного уравнения, значит, частное решение 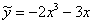 найдено правильно.
найдено правильно.
12. Основные понятия о дифференциальных уравнениях n-ого порядка
Линейным дифференциальным уравнением n-го порядка называется уравнение, в которое неизвестная функция y(x) и её производные входят линейно, т.е. в первой степени:
 .
.
Если старший коэффициент q0 (x) отличен от нуля на интервале (a, b), т.е. 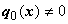 для
для 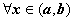 , то, умножая уравнение на
, то, умножая уравнение на 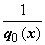 , приводим уравнение к виду со старшим коэффициентом, равным 1:
, приводим уравнение к виду со старшим коэффициентом, равным 1:
 (20)
(20)
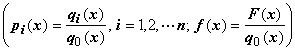 ;
;
дальше мы будем рассматривать уравнение (20).
Если правая часть уравнения тождественно равна нулю на рассматриваемом интервале (f(x)=0 при 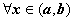 ), то уравнение называется однородным.
), то уравнение называется однородным.
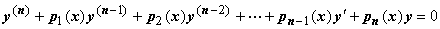 . (21)
. (21)
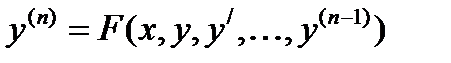 (1)
(1)
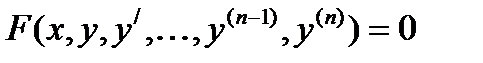 (2)
(2)
Если уравнение разрешимо относительно старшей производной то имеет вид (1). Так же уравнение n-го порядка можно представить в виде системы из n уравнений первого порядка.
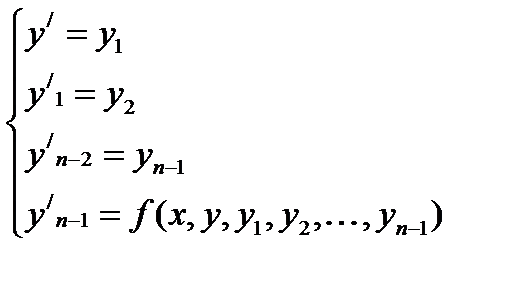 (3)
(3)
Для уравнения n-ого порядка выполнены условия теоремы о существовании и единственности для системы так как (1)~(2)~(3).
Простейшие случаи понижения порядка.
1. Уравнение не содержат искомой функции и ее производной до порядка k-1 включительно, то есть
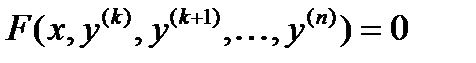 . (4)
. (4)
В этом случае порядок может быть понижен до  заменой
заменой  . Если из этого уравнения выразить
. Если из этого уравнения выразить 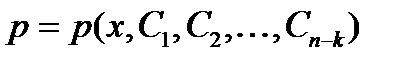 тогда решение y можно определить k-кратным интегрируемым функции p.
тогда решение y можно определить k-кратным интегрируемым функции p.
Пример.
 .
.
2. Уравнение, не содержащие неизвестного переменного 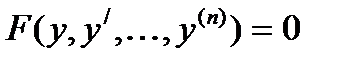 (5)
(5)
В этом случае порядок можно понизить на единицу подстановкой
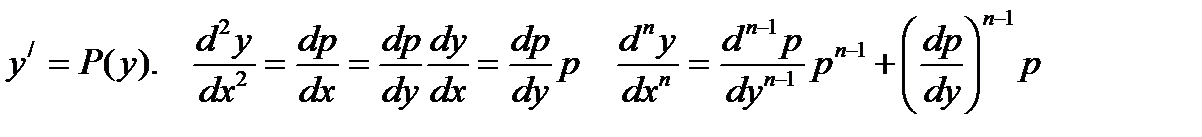 .
.
Пример.
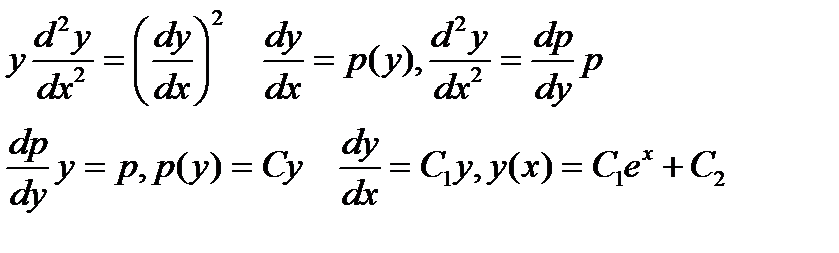
3. Левая часть уравнения
 (6)
(6)
есть производная некоторого дифференциального выражения (n-1)-го порядка. 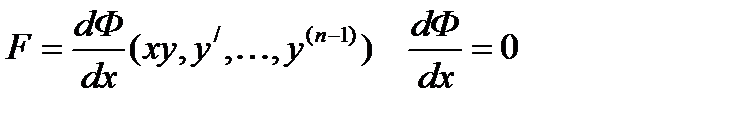 . Если
. Если 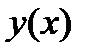 - решение последнего уравнения, следовательно, существует
- решение последнего уравнения, следовательно, существует 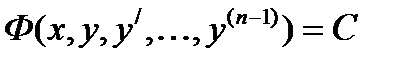 . Мы получили первый интеграл уравнения (6) и понизили на единицу степень решаемого уравнения.
. Мы получили первый интеграл уравнения (6) и понизили на единицу степень решаемого уравнения.
|
|
Замечание. Иногда левая часть (6) становится производной дифференциального уравнения (n-1)-го порядка только при умножении на  поэтому здесь могут появиться лишнее решения (обращающие
поэтому здесь могут появиться лишнее решения (обращающие 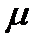 в ноль) или мы можем потерять решение, если
в ноль) или мы можем потерять решение, если 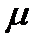 разрывная функция.
разрывная функция.
Пример.
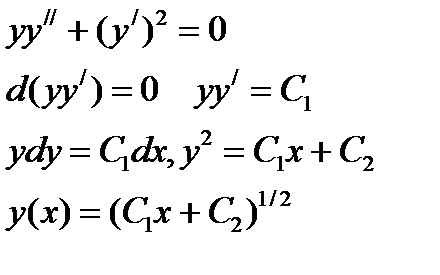
4. Уравнение
 (7)
(7)
однородно относительно 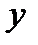 и его производных.
и его производных.
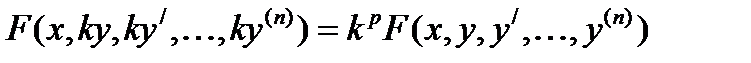 .
.
Или 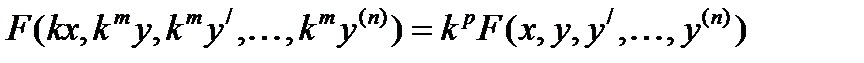 , где показатель
, где показатель  определяется из условий однородности.
определяется из условий однородности.
Порядок этого уравнения может быть понижен на единицу заменой:
 .
.
Если подставить эти соотношения в (7) и учесть однородность функции F , то в итоге в получим:
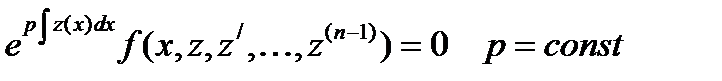 .
.
Пример.
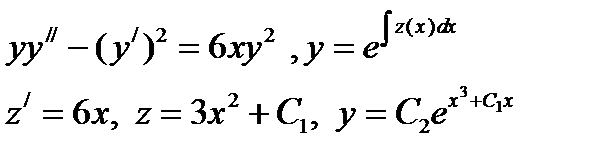 .
.
13. Определитель Вронского. Критерий линейной независимости системы решений однородного ОДУ
1) Определителем Вронского W(x; y1(x), y2(x), ..., ym(x)) называется определитель, первая строка которого образована функциями y1(x),y2(x), ..., ym(x) из Cm-1[a, b] , а последующие строки образованы производными от функций предыдущей строки:
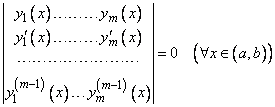
Доказательство: Так как функции 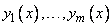 линейно зависимы на
линейно зависимы на  , то существуют такие не все равные нулю числа
, то существуют такие не все равные нулю числа 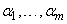 , при которых выполняется тождество
, при которых выполняется тождество  на
на  . Дифференцируя его
. Дифференцируя его 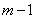 раз, получим систему уравнений
раз, получим систему уравнений

Эта однородная система по условию имеет нетривиальное решение 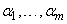 (т. е. хотя бы одно
(т. е. хотя бы одно 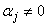 ) при
) при 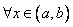 . Последнее возможно, когда определитель системы, который является определителем Вронского
. Последнее возможно, когда определитель системы, который является определителем Вронского  , тождественно равен нулю. Теорема доказана.
, тождественно равен нулю. Теорема доказана.
2) Функции y1(x), y2(x), ..., yn(x) называются линейно независимыми на отрезке [a,b], если существуют постоянные α1, α2, ..., αn равные нулю, такие, что для всех значений x из этого отрезка справедливо тождество

Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функции y1(x), y2(x) будут линейно независимыми на отрезке [a,b], если их отношение на данном отрезке тождественно не равно постоянной:

14. Фундаментальная система решений. Теорема о структуре общего решения линейного однородного уравнения n-го порядка
Функции 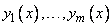 называются линейно зависимыми на
называются линейно зависимыми на  , если существуют числа
, если существуют числа 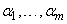 , из которых хотя бы одно не равно нулю, такие, что
, из которых хотя бы одно не равно нулю, такие, что  . (4)
. (4)
|
|
Если тождество (4) выполняется лишь в случае, когда все 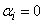 , то функции
, то функции  называются линейно независимыми на
называются линейно независимыми на  . Система из
. Система из 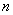 линейно независимых на интервале
линейно независимых на интервале  решений
решений 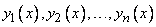 однородного дифференциального уравнения
однородного дифференциального уравнения 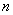 -го порядка (3) с непрерывными на
-го порядка (3) с непрерывными на  коэффициентами
коэффициентами 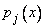 называется фундаментальной системой решений этого уравнения.
называется фундаментальной системой решений этого уравнения.
Чтобы решить линейное однородное дифференциальное уравнение 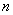 -го порядка (3) с непрерывными коэффициентами
-го порядка (3) с непрерывными коэффициентами 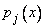 , надо найти его фундаментальную систему решений.
, надо найти его фундаментальную систему решений.
Согласно теореме, произвольная линейная комбинация из решений 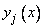 , т. е. сумма
, т. е. сумма
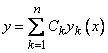 , (5)
, (5)
где  - произвольные числа, есть в свою очередь решение уравнения (3) на
- произвольные числа, есть в свою очередь решение уравнения (3) на  . Таким образом, общее решение однородного дифференциального уравнения (3) имеет вид (5), где
. Таким образом, общее решение однородного дифференциального уравнения (3) имеет вид (5), где  - произвольные постоянные, а
- произвольные постоянные, а 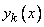 - частные решения (3), образующие фундаментальную систему решений однородного уравнения.
- частные решения (3), образующие фундаментальную систему решений однородного уравнения.
15. Разностные уравнения, определение порядка уравнения
РАЗНОСТНЫЕ УРАВНЕНИЯ [difference equations] — уравнения, содержащие конечные разности искомой функции. (Конечная разность определяется как соотношение, связывающее дискретный набор значений функции y = f(x), соответствующих дискретной последовательности аргументов x1, x2, ..., xn.) В экономических исследованиях значения величин часто берутся в определенные дискретные моменты времени. Напр., о выполнении плана судят по показателям на конец планируемого периода. Поэтому вместо скорости изменения какой-либо величины df/dt приходится брать среднюю скорость за определенный конечный интервал времени Δf/Δt. Если выбрать масштаб времени так, что длина рассматриваемого периода равна 1, то скорость изменения величины можно представить как разность
y = y(t+1) – y(t),
которую часто называют первой разностью. При этом различают правую и левую разности, в частности
y = y(t) – y(t–1)
— левая, а приведенная выше — правая. Можно определить вторую разность:
Δ(Δy) = Δy(t + 1) – Δy(t) = y(t + 2) –
– 2y(t + 1) + y(t)
и разности высших порядков
Δn=Δ(Δ(n-1)*y(x)).
Теперь можно определить Р. у. как уравнение, связывающее между собой конечные разности в выбранной точке:
|
|
f [y(t), Δy(t), ..., Δny(t)] = 0.
Р. у. всегда можно рассматривать как соотношение, связывающее значения функции в ряде соседних точек
y(t), y(t+1), ..., y(t+n).
При этом разность между последним и первым моментами времени называется порядком уравнения.
При численном решении дифференциальных уравнений их часто заменяют разностными. Это возможно, если решение Р. у. стремится к решению соответствующего дифференциального уравнения, когда интервал Δt стремится к нулю.
16. Общий вид решения уравнения вида y(t+1) – y(t) = f(t)
y(t+1) – y(t) = f(t)
∆y(t)=f(t)
t=0: y(1)-y(0)=f(0) => y(1)=f(0)+y(0)
t=1: y(2)-y(1)=f(1) => y(2)=f(1)+y(1) t=k: y(k)=y(0)+  =C+
=C+ 
17. Общий вид решения уравнения y(t+1) = y(t)*p(t)
y(t+1) = y(t)*p(t)
y(1)=p(0)*y(0)
y(2)= p(1)*y(1)= p(1)*p(0)*y(0)
k-1 k-1
y(k)=  p(m)*y(0)= C*
p(m)*y(0)= C*  p(m)
p(m)
m=0 m=0
18. Общий вид решения уравнения y(t+1) = y(t) * p(t) + f(t)
y(t+1) = y(t) * p(t) + f(t)
y(t)=u(t)*v(t)
u(t+1)*v(t+1)-p(t)*u(t)*v(t)-f(t)=0
u(t+1)*(v(t+1)-v(t)-v(t)*(p(t)u(t)u(t)-u(t+1)-t(t)=0
u(t+1)=p(t)u(t)
k-1
u(k)=C*  p(m)
p(m)
m=0
t
v(t+1)-v(t)=f(t)/u(t+1)= f(t)/ C*∏(m)=g(t)
m=0
v(t+1)=v(t)+g(t)
t
v(t+1)=C2 + Σg(k)
k=0
t k
v(t+1)=C2 + Σ f(k)/C1 ∏ p(m)
k=0 m=0
t-1 k
v(t)=C2 + Σ f(k)/C1 ∏ p(m)
k=0 m=0
k-1
u(t)=C1 ∏ p(m)
m=0
t-1 k-1
y(t)=u(t)*v(t)= (C2 + Σ f(k)/C1 ∏ p(m)
k=0 m=0
19. Фундаментальная система решений однородного разностного уравнения с постоянными коэффициентами
Фундаментальной системой решений однородного линейного разностного уравнения называется упорядоченный набор из n линейно независимых решений уравнения или, проще говоря, Фундаментальными решениями уравнения называют такие решения, из которых можно сконструировать все остальные решения.
Между линейными дифференциальными уравнениями n-го порядка и линейными разностными уравнениями n-го порядка много общего.
| Фундаментальная система решений | |
1)  решения л.о, D:y
2) решения л.о, D:y
2)  л.н.з., т.е л.н.з., т.е
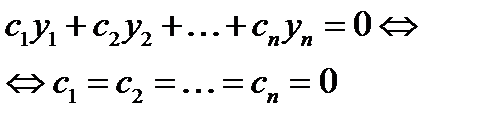 Необходимое и достаточное условие
Необходимое и достаточное условие
| 1) 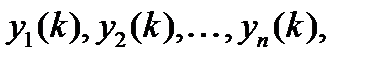 решение л. о. Р. у
2) решение л. о. Р. у
2) 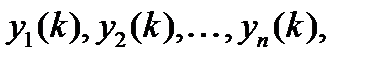 л.н.з л.н.з
 Необходимое и достаточное условие
Необходимое и достаточное условие
|
Рассмотрим следующие случаи для построения фундаментальной системы решений(ф.д.м.)
1) 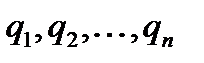 -различные вещественные корни
-различные вещественные корни
Ф.С.Р, 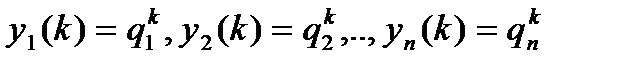
2) Среди вещественных корней есть кратные qi-кратность ri

 соответствующие частные решения
соответствующие частные решения
3) Если

4. Если  -корни кратности «r», то получаем «2r» частных решений:
-корни кратности «r», то получаем «2r» частных решений:
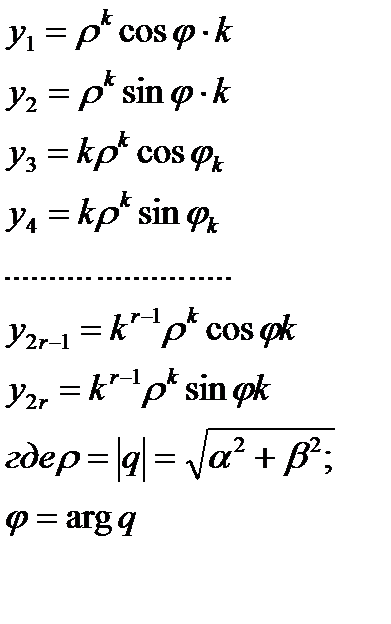
Заметим, что в любом случае Ф.С.Р. состоит из «n» частных решений
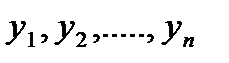
Тогда общее решение однородных уравнений:
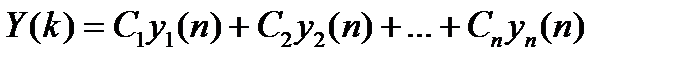
20. Общий вид решения неоднородного разностного уравнения с постоянными коэффициентами
Пусть задано неоднородное разностное уравнение /см.(2)/
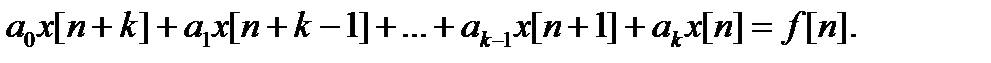
Требуется определить решение уравнения, удовлетворяющее начальным условиям 
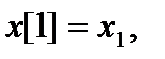 ....,
...., 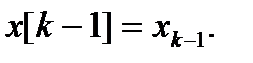
Последовательность решения разностного уравнения (2) такова:
1. Найти общее решение  однородного уравнения
однородного уравнения
|
|
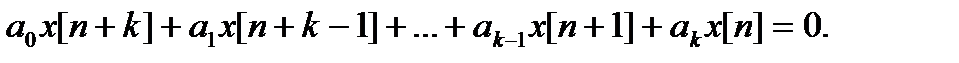
2. Найти частное решение 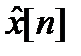 неоднородного уравнения.
неоднородного уравнения.
3. Записать общее решение неоднородного уравнения
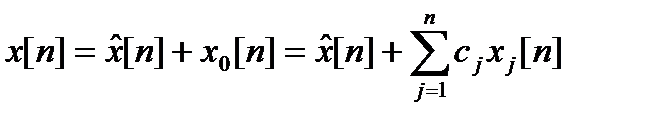 ,
,
где 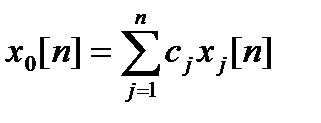 - общее решение однородного уравнения
- общее решение однородного уравнения
4. Определить постоянные С1 , С2 , ... , Сk, используя заданные начальные условия.
Пример 7. Найти решение неоднородного уравнения
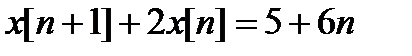
удовлетворяющее начальному условию  .
.
Решение. 1.Частное решение неоднородного уравнения имеем в виде
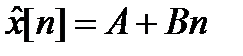
подставляем 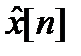 в уравнение
в уравнение
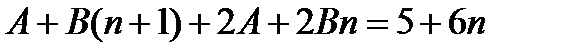 ;
;
 ;
;
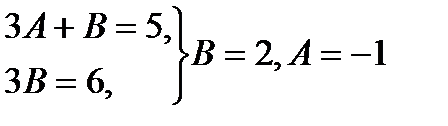 ,
,
Следовательно 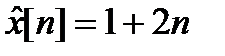 .
.
2. Общее решение однородного уравнения:
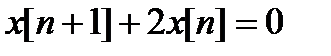 ,
,  ,
, 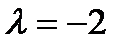 ;
;
частное решение 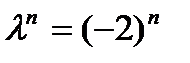 ;
;
общее решение:  .
.
3. Общее решение неоднородного уравнения:
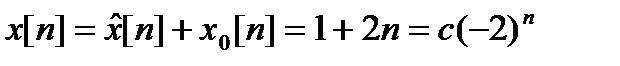 .
.
4.
5. Определяем постоянную С:
 .
.
Искомое решение имеет вид
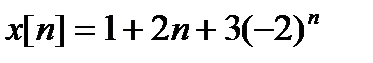 .
.
Пример 8. Найти решение неоднородного разностного уравнения
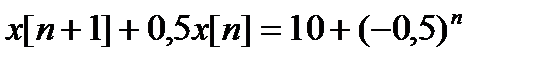
удовлетворяющее начальному условию 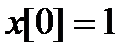 .
.
Решение. 1.Частное решение неоднородного уравнения ищем в виде
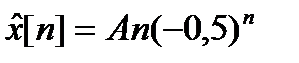 ,
,
подставляем 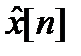 в исходное уравнение
в исходное уравнение
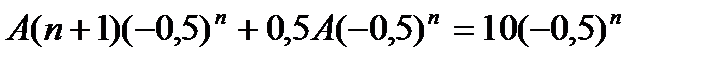 ;
;
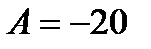
Следовательно  .
.
2. Общее решение однородного уравнения:
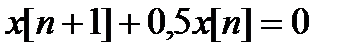 ,
,  ,
, 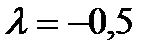 ;
;
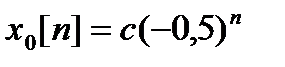 .
.
3. Общее решение неоднородного уравнения:
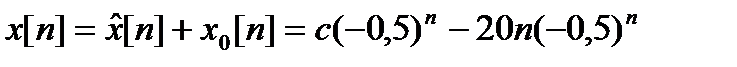 .
.
6. Определяем постоянную С:
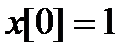 , т.е. С=1.
, т.е. С=1.
Искомое решение имеет вид
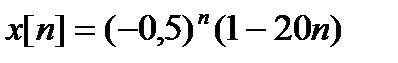 .
.
|
|
|

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!